2022年华数杯数学建模B题水下机器人的组装计划解题全过程文档及程序
2022年华数杯全国大学生数学建模
B题 水下机器人的组装计划
原题再现:
自来水管道清理机器人(Water pipe cleaning robot,简称WPCR)是一种可在水下移动、具有视觉和感知系统、通过遥控或自主操作方式、使用机械臂代替或辅助人去完成自来水管道垃圾清理任务的装置。运用这种装置能够及时清理管道,既可提高自来水的品质,也能够保证水流畅通,因而越来越受到水务公司和家庭住户的青睐。
某工厂生产的WPCR装置需要用 3 个容器艇(用A表示)、4 个机器臂(用B表示)、5 个动力系统(用C表示)组装而成。每个容器艇(A)由 6 个控制器(A1)、8 个划桨(A2)和 2 个感知器(A3)组成。每个机器臂(B)组成比较复杂,简单可划分为 2 个力臂组件(B1)和 4 个遥感器(B2)组成。每个动力系统(C)由 8 个蓄电池(C1)、2 个微型发电机(C2)和 12 个发电螺旋(C3)组成。也就是说组装一个完整的WPCR装置,需要 3 个容器艇(A),包括 18 个控制器(A1)、24 个划桨(A2)以及 6 个感知器(A3)。组装一台WPCR需要的其他部件数以此类推。组装WPCR所需要的产品统称为组件,包括A和A1、A2、A3,B和B1、B2,C和C1、C2、C3。
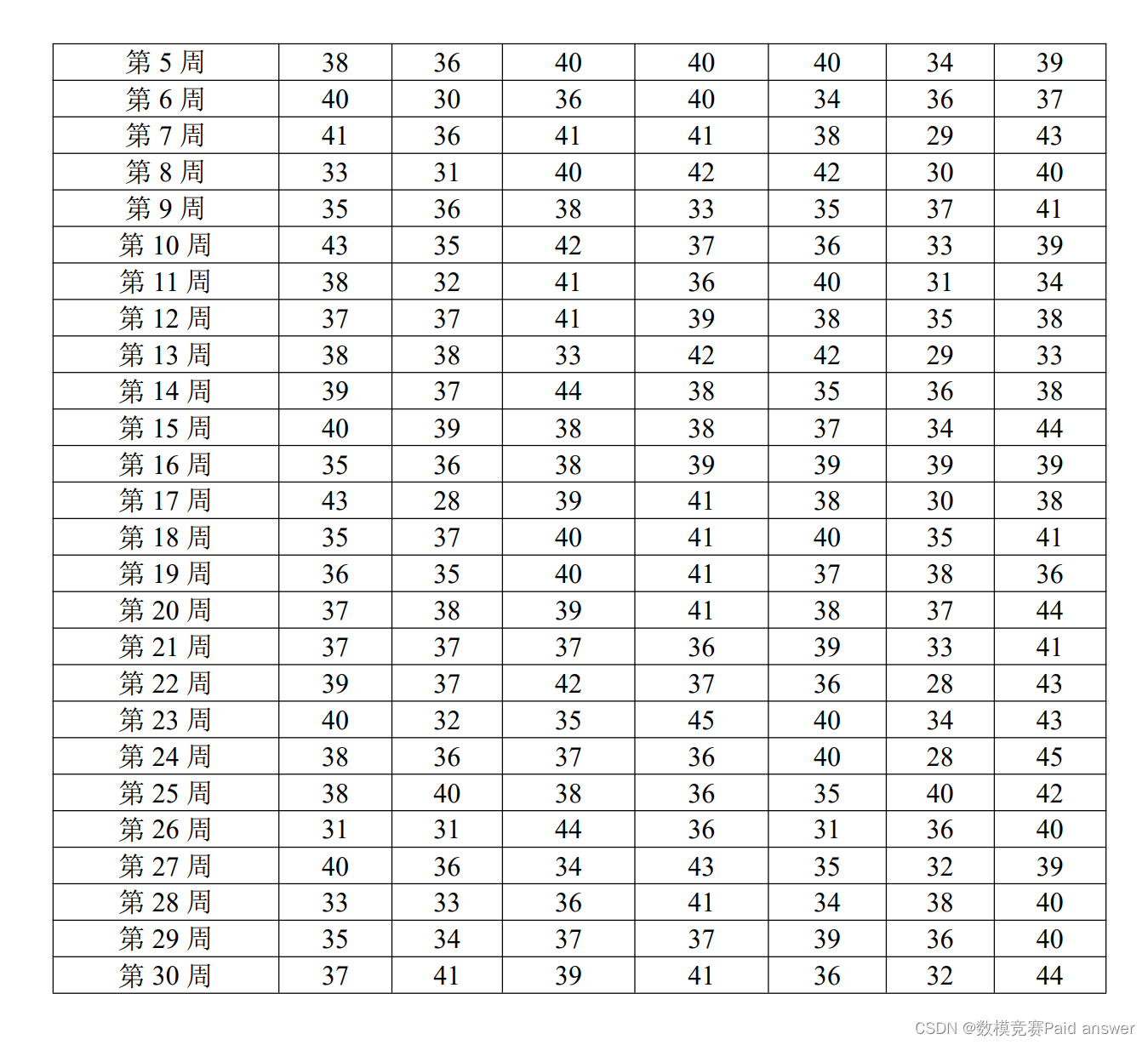
该工厂每次生产计划的计划期为一周(即每次按照每周 7 天的订购数量实行订单生产),只有最终产品WPCR有外部需求,其他组件不对外销售。容器艇(A)、机器臂(B)、动力系统(C)生产要占用该工厂最为关键的设备,因而严格控制总生产工时。A、B、C的工时消耗分别为 3 时/件、5 时/件和 5 时/件,即生产 1 件A需要占用 3 个工时,生产 1 件B需要占用 5 个个工时,生产 1 件C需要占用 5 个工时。每天的WPCR外部需求数及关键设备总工时限制见表 5。
为了顺利生产WPCR,工厂在某一天生产组件产品时,需要付出一个与生产数量无关的固定成本,称为生产准备费用。比如第一天生产了A,则要支付A的生产准备费用,若第二天再生产A,则需要再支付A的生产准备费用。如果某一天结束时某组件有库存存在,则工厂必须付出一定的库存费用(与库存数量成正比)。数据见表 6。另外,按照工厂的信誉要求,目前接收的所有订单到期必须全部交货,轻易不能有缺货事件发生。
请回答下列问题。
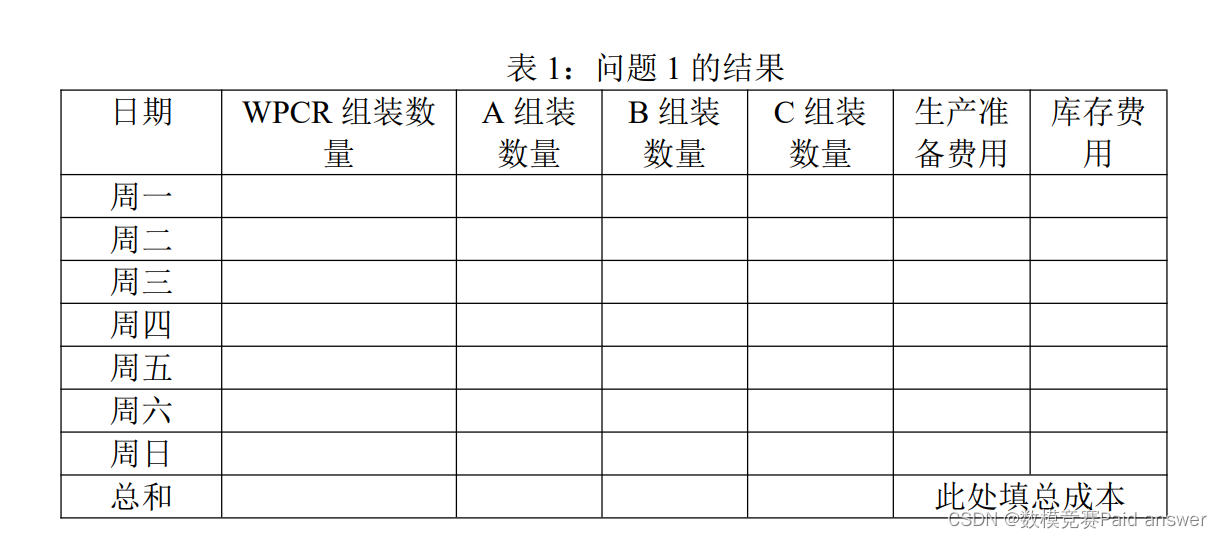
1. 若该工厂第一天(周一)开始时没有任何组件库存,也不希望第 7 天(周日)结束后留下任何组件库存。每天采购的组件马上就可用于组装,组装出来的组件也可以马上用于当天组装成WPCR。若要求总成本最小,请问如何制定每周 7 天的生产计划?将结果填入表 1。
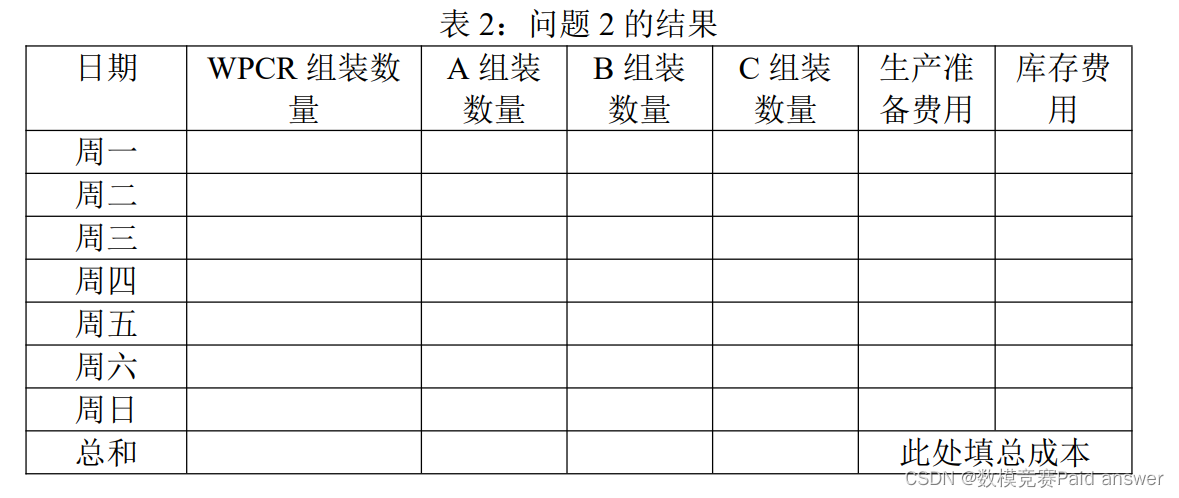
2. 然而,事实上,组件A、B、C需要提前一天生产入库才能组装WPCR,A1、A2、A3、B1、B2、C1、C2、C3 也需要提前一天生产入库才能组装A、B、C。在连续多周生产情况下,需要统筹规划。比如在周一生产WPCR前一天(上周周日)必须事先准备好组件库存,而且在本周日必须留下必要的组件库存用以保障下周一的生产。每周的WPCR需求和关键设备工时限制以及每次生产准备费用和单件库存费用数据见表 5、表6,请问如何制定每周 7 天的生产计划以求总成本最低?将结果填入表 2
3. 接问题 2。为了保障生产的持续性,工厂需要在 30 周 210 天里必须设置 7 次停工检修,每次检修时间为 1 天。检修之后关键设备生产能力有所提高,检修后的第一天A、B、C生产总工时限制将会放宽 10%,随后逐日减少放宽 2%的比例,直至为 0(如第一天放宽 10%,第二天就放宽 8%,…)。检修日的订单只能提前安排生产,当天不能生产任何组件。假设每周的关键设备工时限制以及每次生产准备费用和单件库存费用数据不变,任意两次检修之间要相隔 6 天以上,请问,检修日放在哪几天最为合适(总成本最小)?将结果填入表 3(填天的序号即可,如 26,就表示是第 26 天)。30 周的WPCR外部需求数据见表 7。

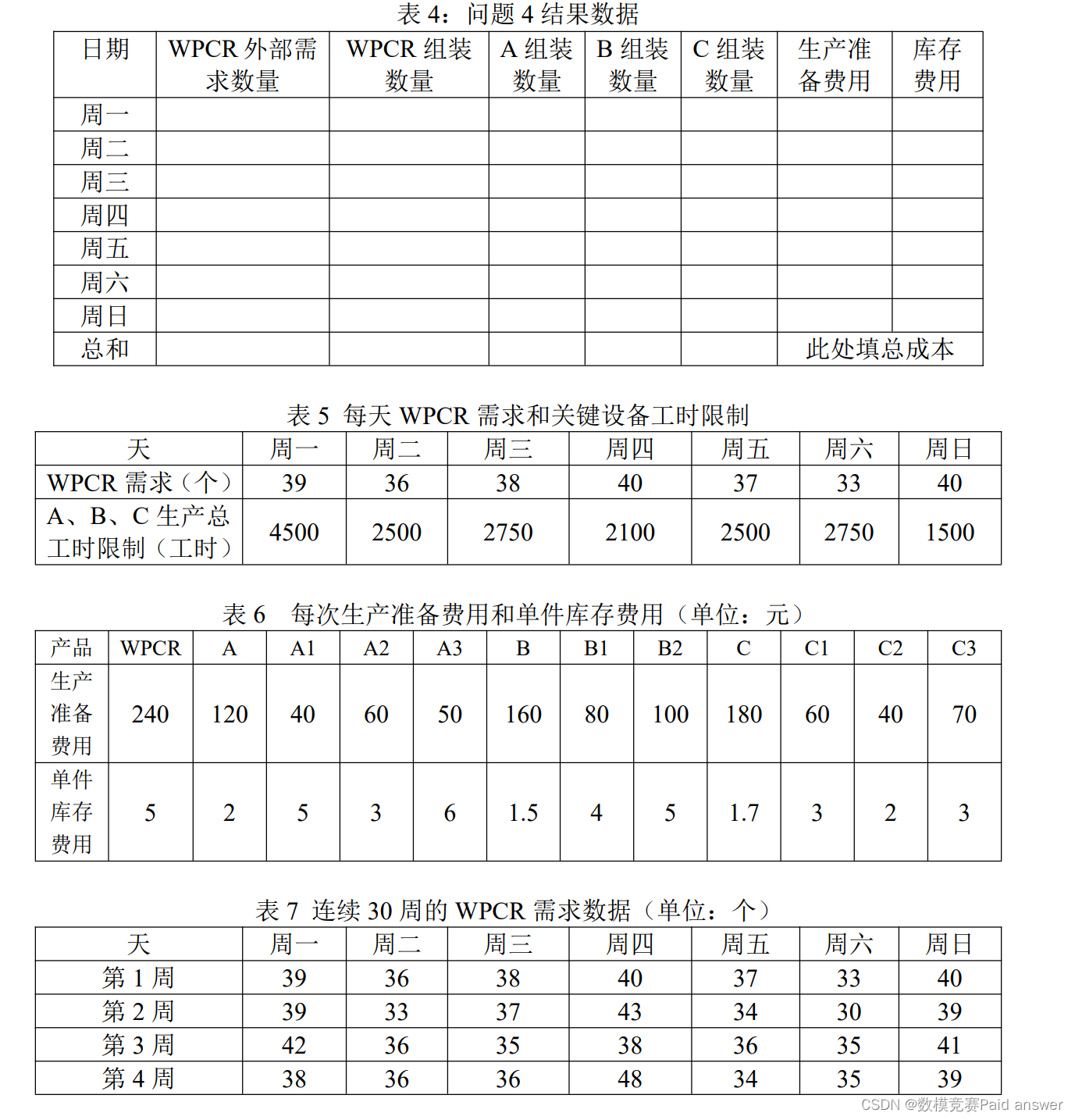
4. 在生产实际中,在未知WPCR外部需求订单的前提下,公司需要有一个稳妥的单周生产计划。接问题 2,表 7 数据视为历史周订单数据,在不知未来某周 7 天订单数且继续追求周总成本最小的前提下,如何制定周生产计划,既能够保障每天的WPCR订单均以 95%以上的概率保证正常交付,又能够以 85%以上的概率保证整周的WPCR订单能正常交付?将结果填入表 4。
整体求解过程概述(摘要)
本文研究某工厂水下机器人的生产计划,通过建立基于整数规划的单周生产优化模型,求出生产组件直接用于组装的单周生产计划;建立基于整数规划的多周生产优化模型,求出组件需提前一天生产才可使用的多周生产计划;建立检修点选取模型设置 7 个检修日;改编基于整数规划的多周生产优化模型对设置检修日后的生产计划和最低成本进行求解;建立基于正态分布的需求量预设模型,得出需求量的合理预设。
针对问题一,建立了基于整数规划的单周生产优化模型。首先,根据题目数据计算每天至少需要的 A、B、C 数量;再以总成本最低为目标函数,以需求量、工时、库存为约束条件,建立基于整数规划的单周生产优化模型,利用 MATLAB 编程求最优解得到每天所需的生产准备费用及剩余组件所需的库存费用,再总结 WPCR 和组件 A、B、C每天的组装数量,以及所需的总成本,所得单周所需生产准备费用为 8400 元,库存费用为 216 元,最低总成本为 8616 元。
针对问题二,建立了基于整数规划的多周生产优化模型。首先,分析问题二大、小件均需提前一天生产入库才可进行组装造成结果的两种情况;再以总成本最低为目标函数,需求量约束、工时约束、库存约束为约束条件,建立基于整数规划的多周生产优化模型,求解得到总成本最低时,一周中每天组件 A、B、C、A1 、A2、A3 、B1 、B2 、C1、C2、C3 和 WPCR 的生产或组装情况;再计算得出该生产计划下每周所需要的生产准备费用为 2930 元、库存费用为 175272.4 元,最低总成本为 178202.4 元。
针对问题三,建立了基于整数规划的检修点选取模型。首先,进行检修点的选取,以前 6 天与后 5 天剩余工时之差为目标,检修日范围限制及检修日间隔限制为约束,建立检修点求取模型,得到检修日的时间安排;再求解最低总成本,第一部分为不受检修日影响的日期;第二部分为所有检修日的前 6 天,将检修日的需求量按剩余工时比例分配给它的前 6 天;第三部分为检修日的后 5 天,因检修日影响了工时限制。三部分分别改编问题二模型中的目标函数和约束条件,求解该安排下的最低总成本为 5359292.9 元。
针对问题四,建立了基于正态分布的需求量预设模型。首先,对 30 周需求量的历史数据进行正态概率分析并绘制正态概率图,得出需求量每周一至周日和每周均服从正态分布;再建立基于正态分布的需求量预设模型,根据 3σ 原则和数值分布计算,得到满足题目要求的周需求量;再根据每天需求量范围最小值权重对周一至周日进行需求量分配;然后根据新的需求量利用问题二模型对生产计划及最低总成本进行计算,得此计划下最低总成本为 174042.8 元。
模型假设:
• 假设每件生产的组件均可进行组装,不存在坏损情况。
• 假设小件组件的生产工时可以忽略不计。
问题分析:
问题一分析
问题一要求在组件可直接用于组装的情况下,制定每周 7 天的生产计划使得总成本最小。首先,根据题目表 5 提供的一周内每天 WPCR 机器人的生产需求量,按照题目给定生产 WPCR 所需生产组件 A、B、C 的比例,计算得到对应每天至少需要的 A、B、C 数量;再以总成本最小为目标函数,以需求量、工时、库存、最后一天库存清零为约束条件,建立基于整数规划 [1−3] 的单周生产优化模型,利用 MATLAB 编程求解整数规划的最优解; 然后通过求解结果总结 WPCR 和组件 A、B、C 每天的组装数量,以及所需的总成本。
问题二分析
问题二要求在大、小组件均需要提前一天生产入库才可进行组装的情况下,制定连续多周 7 天的生产计划使得总成本最小,将结果填入表 2。首先,分析问题二大、小件均需提前一天生产入库才可进行组装的两种情况,其结果可能是生产每三天一批循环叠加,也可能是存在某天无需生产某组件,依靠前一次库存即可完成组装;再以总成本最低为目标,需求量约束、工时约束、库存约束为约束条件,建立基于整数规划 [4−6] 的多周生产优化模型,求解得到总成本最低时,一周每天组件 A、B、C、A1 、A2、A3 、B1、B2 、C1 、C2 、C3 和 WPCR 的生产或组装情况;再计算该生产计划下每周所需要的生产准备费用、库存费用及总成本费用。
问题三分析
问题三要求求解总成本最小时检修日的安排情况,并求得这 30 周的最低总成本。本文将此问题分为两个阶段进行求解。首先,第一阶段求解检修点的选取,基于剩余工时在检修前应尽量多、在检修后应相对少,以前 6 天与后 5 天剩余工时之差为目标函数,以这 210 天的首、未 5 天不可设置检修日限制和检修点之间间隔限制为约束条件,建立基于整数规划 [7,8] 的检修点选取模型,求得 7 次检修日的时间安排。第二阶段求解最低总成本,将已经设置检修日的这 210 天以天为单位划分为三个部分对各部分最低总成本进行求解:
1. 第一部分为不受检修日影响的日期,可通过建立基于整数规划的生产优化模型直接求取该部分生产计划与总成本;
2. 第二部分为所有检修日前 6 天的日期,将检修日的需求量按剩余工时比例分配给它的前六天后,改编问题二基于整数规划的多周生产优化模型中的目标函数和约束条件,利用 MATLAB 整数规划求解该部分的生产计划及最低总成本;
3. 第三部分为所有检修日后 5 天的日期,这部分每天的工时限制会受检修日的影响而不同比例增加,本文通过计算出改变后的工时限制,再次改编问题二模型中的目标函数和约束条件,利用 MATLAB 整数规划求解该部分的生产计划及最低总成本。
问题四分析
问题四要求在不知未来某周 7 天订单数且继续追求周总成本最小的前提下,制定周生产计划,既能够保障每天的 WPCR 订单均以 95% 以上的概率保证正常交付,又能够以 85% 以上的概率保证整周的 WPCR 订单能正常交付, 并将结果填入表 4。首先,对 30周需求量的历史数据进行正态概率分析 [9,10] 并绘制正态概率图,得出需求量每周一至周日和每周均服从正态分布;再建立基于正态分布的需求量预设模型,根据 3σ 原则和数值分布计算,得到满足题目要求的周需求量;再根据每天需求量范围最小值权重对周一至周日进行需求量分配;然后根据新的需求量利用问题二模型对生产计划及最低总成本进行计算。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
论文及程序仅供学习与参考
a=[33 31 40 42 42 30 40];
prob=optimproblem('ObjectiveSense','min');
x=optimvar('x',3,7,'Type','integer','LowerBound',0);
prob.Objective=1200*7+2*(7*(x(1,7)+x(1,1)-3*a(1))+6*(x(1,2)-3*a(2))+5*(x(1,3)
-3*a(3))+4*(x(1,4)-3*a(4))+3*(x(1,5)-3*a(5))+2*(x(1,6)-3*a(6))+x(1,7)-3*a(7))...
+1.5*(7*(x(2,7)+x(2,1)-4*a(1))+6*(x(2,2)-4*a(2))+5*(x(2,3)-4*a(3))
+4*(x(2,4)-4*a(4))+3*(x(2,5)-4*a(5))+2*(x(2,6)-4*a(6))+x(2,7)-4*a(7))...
+1.7*(7*(x(3,7)+x(3,1)-5*a(1))+6*(x(3,2)-5*a(2))+5*(x(3,3)-5*a(3))
+4*(x(3,4)-5*a(4))+3*(x(3,5)-5*a(5))+2*(x(3,6)-5*a(6))+x(3,7)-5*a(7))...
+5*(6*(sum(x(1,:),2)))...
+3*(8*(sum(x(1,:),2)))...
+6*(2*(sum(x(1,:),2)))...
+4*(2*(sum(x(2,:),2)))...
+5*(4*(sum(x(2,:),2)))...
+3*(8*(sum(x(3,:),2)))...
+2*(2*(sum(x(3,:),2)))...
+3*(12*(sum(x(3,:),2)));
prob.Constraints.con1=3*x(1,1)+5*x(2,1)+5*x(3,1)<=4500;
prob.Constraints.con2=3*x(1,2)+5*x(2,2)+5*x(3,2)<=2500;
prob.Constraints.con3=3*x(1,3)+5*x(2,3)+5*x(3,3)<=2750;
prob.Constraints.con4=3*x(1,4)+5*x(2,4)+5*x(3,4)<=2100;
prob.Constraints.con5=3*x(1,5)+5*x(2,5)+5*x(3,5)<=2500;
prob.Constraints.con6=3*x(1,6)+5*x(2,6)+5*x(3,6)<=2750;
prob.Constraints.con7=3*x(1,7)+5*x(2,7)+5*x(3,7)<=1500;
prob.Constraints.con8=x(1,1)+x(1,2)+x(1,3)+x(1,4)+x(1,5)+x(1,6)+x(1,7)>=3*(sum(a));
prob.Constraints.con9=x(2,1)+x(2,2)+x(2,3)+x(2,4)+x(2,5)+x(2,6)+x(2,7)>=4*(sum(a));
prob.Constraints.con10=x(3,1)+x(3,2)+x(3,3)+x(3,4)+x(3,5)+x(3,6)+x(3,7)>=5*(sum(a));
[sol,fval,flag]=solve(prob);
xx=sol.x;
a=[41,36,41,41,38];
prob=optimproblem('ObjectiveSense','min');
x=optimvar('x',3,5,'Type','integer','LowerBound',0);
prob.Objective=1200*5+2*(5*(x(1,5)+x(1,1)-3*a(1))+4*(x(1,2)-3*a(2))+3*(x(1,3)-3*a(3))
+2*(x(1,4)-3*a(4))+1*(x(1,5)-3*a(5)))...
+1.5*(5*(x(2,5)+x(2,1)-4*a(1))+4*(x(2,2)-4*a(2))+3*(x(2,3)-4*a(3))+2*(x(2,4)-4*a(4))
+1*(x(2,5)-4*a(5)))...
+1.7*(5*(x(3,5)+x(3,1)-5*a(1))+4*(x(3,2)-5*a(2))+3*(x(3,3)-5*a(3))+2*(x(3,4)-5*a(4))
+1*(x(3,5)-5*a(5)))...
+5*(6*(sum(x(1,:),2)))...
+3*(8*(sum(x(1,:),2)))...
+6*(2*(sum(x(1,:),2)))...
+4*(2*(sum(x(2,:),2)))...
+5*(4*(sum(x(2,:),2)))...
+3*(8*(sum(x(3,:),2)))...
+2*(2*(sum(x(3,:),2)))...
+3*(12*(sum(x(3,:),2)));
prob.Constraints.con1=3*x(1,1)+5*x(2,1)+5*x(3,1)<=4500*(1+0.1);
prob.Constraints.con2=3*x(1,2)+5*x(2,2)+5*x(3,2)<=2500*(1+0.08);
prob.Constraints.con3=3*x(1,3)+5*x(2,3)+5*x(3,3)<=2750*(1+0.06);
prob.Constraints.con4=3*x(1,4)+5*x(2,4)+5*x(3,4)<=2100*(1+0.04);
prob.Constraints.con5=3*x(1,5)+5*x(2,5)+5*x(3,5)<=2500*(1+0.02);
prob.Constraints.con6=x(1,1)+x(1,2)+x(1,3)+x(1,4)+x(1,5)>=3*(sum(a));
prob.Constraints.con7=x(2,1)+x(2,2)+x(2,3)+x(2,4)+x(2,5)>=4*(sum(a));
prob.Constraints.con8=x(3,1)+x(3,2)+x(3,3)+x(3,4)+x(3,5)>=5*(sum(a));
[sol,fval,flag]=solve(prob);
xx=sol.x;
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
上一篇:Spring整合RabbitMQ
下一篇:Excel-VLOOKUP函数
