数据结构与算法基础-学习-15-二叉树之BST的前序遍历、后序遍历、中序遍历的递归和非递归方法实现
一、二叉树定义
二叉树是N(N>=0)个节点的有限集,它可能是空集或者由一个根节点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。
二、二叉树特点
1、每个节点最多两个孩子。(也就是二叉树的度小于等于2)
2、根有左右之分,不可颠倒。
3、二叉树可以是空集,根的左子树或右子树可以为空。
三、图示
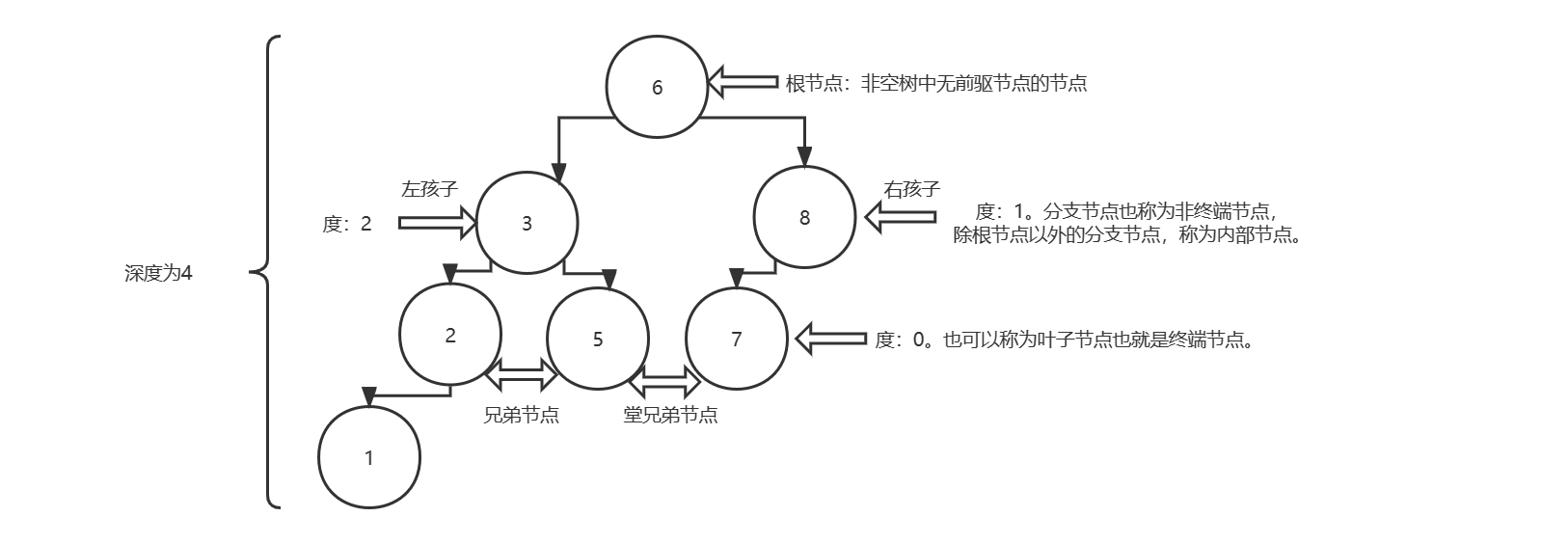
四、二叉树性质
1、性质一
深度为k的二叉树至多有2的k次方再减一。
推导第一层有一个(2的0次方),第二层最多有两个(2的1次方),第三层最多有四个(2的2次方)。我们可以用等比求和公式:Sn=(a1-an*q)/(1-q)=(1-4*2)/(-1)=7。
2、性质二
在二叉树的第i层上至多有2的(i-1)次方个节点。
3、性质三
对任何一棵二叉树T,如果其叶子数为n0,度为2的节点数为n2,n0=n2+1。
五、特殊形式的二叉树
1、满二叉树
(1)定义和图示
满二叉树在相同深度的二叉树中结点数和叶子结点数是最多的。
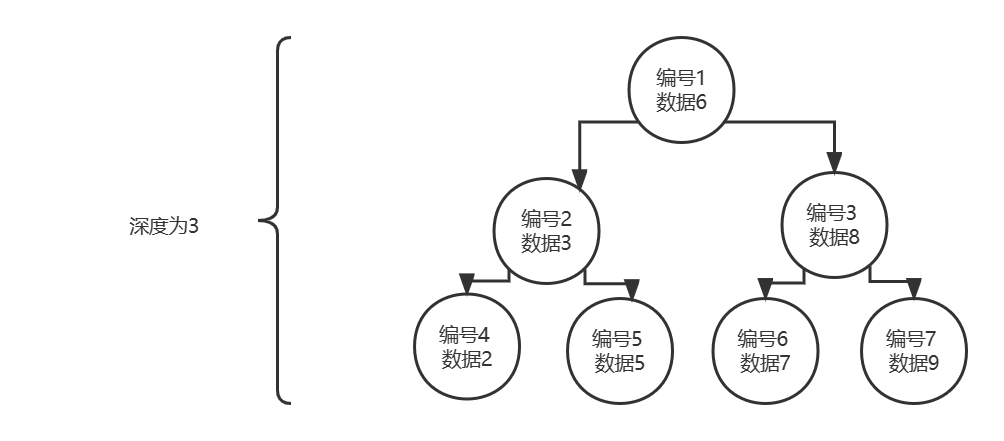
2、完全二叉树
(1)定义和图示
深度为k的具有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时,称之为完全二叉树。
满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
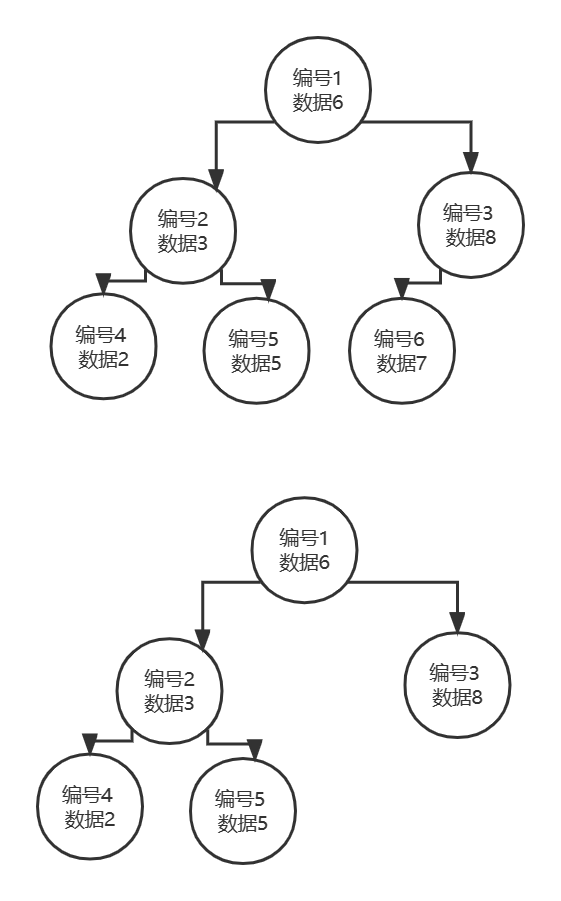
(2)特性一
具有n个结点的完全二叉树深度为log(2)(n)(向下取整)+1。
(3)特性二
如果对一棵有n个结点的完全二叉树(深度为log(2)(n)(向下取整)+1)的结点按照层序编号(从上到下,从左到右),则对于任一结点i(1<=i<=n),有:
(1)如果i=1,则结点i是二叉树的根,无双亲。如果是i>1,则双亲是结点i/2再向下取整。
(2)如果2i>n,则结点i为叶子节点,无左孩子;否则,其左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子。否则,其右孩子是结点2i+1。
六、二叉搜索树
二叉搜索树(Binary Search Tree)简称BST,如果结点的左子树不为空,则左子树存储的数据需要小于结点存储的数据。如果结点的右子树不为空,则右子树存储的数据需要大于结点存储的数据。
二叉搜索树的中序遍历,最终会形成一个从小到大排列的数组。
将数组{6,3,8,2,5,1,7}变为一棵BST,BST如下图:
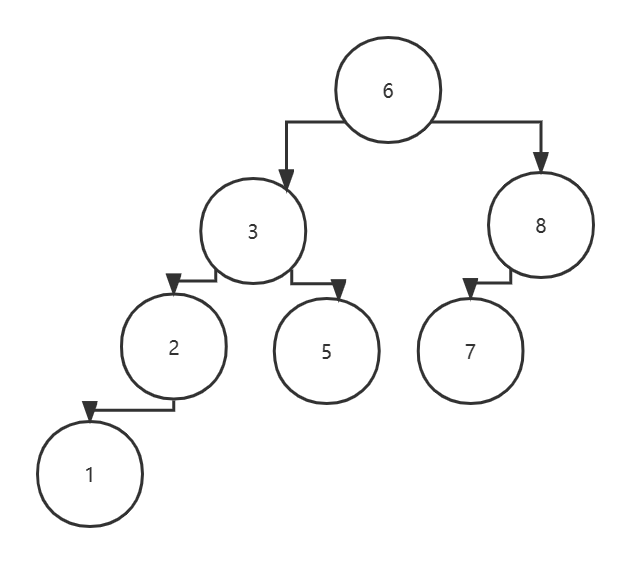
七、BST结构体
1、BinaryTreeNode
(1)描述
二叉树结点定义,Data数据域,LeftNodePtr左子树指针,RightNodePtr右子树指针,JudegeTreeUsedArray在非递归后续遍历时用到,其他并未用到,数组长度2,分别表示左右子树状态
,JUDGE_TREE_UNUSED为此树没遍历,JUDGE_TREE_USED为此树遍历。
(2)定义
#define JUDGE_TREE_UNUSED 0
#define JUDGE_TREE_USED 1
#define JUDGE_TREE_ARRAY_LEN 2typedef int ElemType;typedef struct BinaryTreeNode
{ElemType Data;struct BinaryTreeNode* LeftNodePtr;struct BinaryTreeNode* RightNodePtr;int JudegeTreeUsedArray[JUDGE_TREE_ARRAY_LEN];//为了实现非递归后序遍历使用的数据,其他遍历方法未使用。
}BinaryTreeNode, *BinaryTreeNodePtr;2、BinaryTree
(1)描述
二叉树结点定义,NodePtr树的根节点,TreeNodeNum树的总结点数。
(2)定义
typedef struct BinaryTree
{BinaryTreeNodePtr NodePtr;BinaryTreeSizeType TreeNodeNum;
}BinaryTree;八、BST函数
其中前中后序遍历非递归方法实现需要用到顺序栈,可以参考之前写的博客《数据结构与算法基础-学习-09-线性表之栈的理解、初始化顺序栈、判断顺序栈空、获取顺序栈长度的实现》和《数据结构与算法基础-学习-10-线性表之顺序栈的清理、销毁、压栈、弹栈》
1、NewBinaryTreeNode
(1)描述
生成一个新节点,把数据放入结点中。
(2)定义
BinaryTreeNodePtr NewBinaryTreeNode(ElemType InputData)
{BinaryTreeNodePtr NewNodePtr = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));NewNodePtr->Data = InputData;NewNodePtr->LeftNodePtr = NULL;NewNodePtr->RightNodePtr = NULL;memset(NewNodePtr->JudegeTreeUsedArray, JUDGE_TREE_UNUSED, sizeof(int) * JUDGE_TREE_ARRAY_LEN);//非递归前序遍历使用Log("New Binary Tree Node : OK\n",Debug);return NewNodePtr;
}(3)参数介绍
参数名 | 描述 |
InputData | ElemType类型的数据。 |
2、GetBinaryTreeNodeNum
(1)描述
获取BST的总结点数。
(2)定义
BinaryTreeSizeType GetBinaryTreeNodeNum(BinaryTree* BT)
{JudgeAllNullPointer(BT);return BT->TreeNodeNum;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST指针。 |
3、CmpElemTypeData
(1)描述
对比ET1和ET2的大小。
(2)定义
#define LARGE_FLAG 0
#define LITTLE_FLAG 1
#define EQUAL_FLAG 2Status CmpElemTypeData(ElemType ET1, ElemType ET2)
{if(ET1 > ET2){return LARGE_FLAG;}else if(ET1 < ET2){return LITTLE_FLAG;}else{return EQUAL_FLAG;}
}(3)参数介绍
参数名 | 描述 |
ET1 | ElemType类型数据。 |
ET2 | ElemType类型数据。 |
4、AddBinarySearchTreeNode
(1)描述
将InputData数据放入BST中。
(2)定义
//假设二叉搜索树中没有相同元素,且数据都是正数,根节点大于左子树,小于右子树。
Status AddBinarySearchTreeNode(BinaryTree* BT, ElemType InputData)
{JudgeAllNullPointer(BT);if(BT->NodePtr == NULL){BT->NodePtr = NewBinaryTreeNode(InputData);BT->TreeNodeNum++;Log("Add BST Node : OK\n",Debug);return SuccessFlag;}BinaryTreeNodePtr TmpPtr = BT->NodePtr;while(TmpPtr){if(CmpElemTypeData(TmpPtr->Data, InputData) == LARGE_FLAG){if(TmpPtr->LeftNodePtr == NULL){TmpPtr->LeftNodePtr = NewBinaryTreeNode(InputData);BT->TreeNodeNum++;Log("Add BST Node : OK\n",Debug);return SuccessFlag;}TmpPtr = TmpPtr->LeftNodePtr;}else if(CmpElemTypeData(TmpPtr->Data, InputData) == LITTLE_FLAG){if(TmpPtr->RightNodePtr == NULL){TmpPtr->RightNodePtr = NewBinaryTreeNode(InputData);BT->TreeNodeNum++;Log("Add BST Node : OK\n",Debug);return SuccessFlag;}TmpPtr = TmpPtr->RightNodePtr;}else{Log("AddBinarySearchTreeNode function not supported : same element.\n",Debug);Log("Add BST Node : Fail\n",Debug);return FailFlag;}}return FailFlag;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST。 |
InputData | ElemType类型的输入数据。 |
5、NewBinarySearchTree
(1)描述
给一个数组生成一棵BST。
(2)定义
Status NewBinarySearchTree(BinaryTree* BT, ElemType* Array)
{BinaryTreeSizeType i; for(i = 0; i < InsertDataArrayLen; i++){AddBinarySearchTreeNode(BT, Array[i]);}Log("New Binary Search Tree: OK\n",Info);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST。 |
Array | ElemType*类型的输入数据数据。 |
6、InitBinaryTree
(1)描述
初始化二叉树。
(2)定义
Status InitBinaryTree(BinaryTree* BT)
{JudgeAllNullPointer(BT);BT->TreeNodeNum = 0;Log("Init Binary Tree : OK\n",Info);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST。 |
7、InOrderTraverseNoRecursion
(1)描述
中序遍历非递归方法实现。
(2)定义
Status InOrderTraverseNoRecursion(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}SqStack* S = (SqStack*)MyMalloc(sizeof(SqStack));BinaryTreeNodePtr TmpPtr = RootPTR;InitSqStack(S);while(TmpPtr || JudgeSqStackIsEmpty(S) == FailFlag)//如果指针和栈为空退出循环{if(TmpPtr)//如果节点不为空,说明有数据,中序遍历:左根右。将根压入栈,指针指向左子树。{PushSqStack(S, *TmpPtr);TmpPtr = TmpPtr->LeftNodePtr;}else//如果节点为空,说明左子树没有数据,弹栈获取上一层节点指针,获取根节点数据,再将指针指向右子树。{BinaryTreeNodePtr TmpPtr1 = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));PopSqStack(S, TmpPtr1);Insert2GlobalArray(&GA,TmpPtr1->Data);TmpPtr = TmpPtr1->RightNodePtr;free(TmpPtr1);TmpPtr1 = NULL;}}DestroyStack(S);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
8、PreOrderTraverseNoRecursion
(1)描述
前序遍历非递归方法实现。
(2)定义
Status PreOrderTraverseNoRecursion(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}SqStack* S = (SqStack*)MyMalloc(sizeof(SqStack));BinaryTreeNodePtr TmpPtr = RootPTR;InitSqStack(S);while(TmpPtr || JudgeSqStackIsEmpty(S) == FailFlag)//如果指针和栈为空退出循环{if(TmpPtr){PushSqStack(S, *TmpPtr);Insert2GlobalArray(&GA,TmpPtr->Data);TmpPtr = TmpPtr->LeftNodePtr;}else{BinaryTreeNodePtr TmpPtr1 = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));PopSqStack(S, TmpPtr1);TmpPtr = TmpPtr1->RightNodePtr;free(TmpPtr1);TmpPtr1 = NULL;}}DestroyStack(S);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
9、PostOrderTraverseNoRecursion
(1)描述
后序遍历非递归方法实现。
(2)定义
Status PostOrderTraverseNoRecursion(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}SqStack* S = (SqStack*)MyMalloc(sizeof(SqStack));BinaryTreeNodePtr TmpPtr = RootPTR;InitSqStack(S);while(TmpPtr || JudgeSqStackIsEmpty(S) == FailFlag)//如果指针和栈为空退出循环{if(TmpPtr && TmpPtr->JudegeTreeUsedArray[0] == JUDGE_TREE_UNUSED){TmpPtr->JudegeTreeUsedArray[0] = JUDGE_TREE_USED;PushSqStack(S, *TmpPtr);TmpPtr = TmpPtr->LeftNodePtr;}else{BinaryTreeNodePtr TmpPtr1 = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));PopSqStack(S, TmpPtr1);if((TmpPtr1->JudegeTreeUsedArray)[JUDGE_TREE_ARRAY_LEN-1] == JUDGE_TREE_USED){//printf("%d %d\n",TmpPtr1->JudegeTreeUsedArray[0],TmpPtr1->JudegeTreeUsedArray[JUDGE_TREE_ARRAY_LEN-1]);Insert2GlobalArray(&GA,TmpPtr1->Data);//PrintfGlobalArray(&GA,"tmp");if(PopSqStack(S, TmpPtr1) == FailFlag)//如果栈是空的,说明已经完成所有节点的遍历,跳出循环。{free(TmpPtr1); TmpPtr1 = NULL;break;}}TmpPtr = TmpPtr1->RightNodePtr;TmpPtr1->JudegeTreeUsedArray[JUDGE_TREE_ARRAY_LEN-1] = JUDGE_TREE_USED;PushSqStack(S, *TmpPtr1);free(TmpPtr1);TmpPtr1 = NULL;}}DestroyStack(S);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
10、InOrderTraverse
(1)描述
中序遍历递归方法实现。
(2)定义
Status InOrderTraverse(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}else{InOrderTraverse(RootPTR->LeftNodePtr);//printf("%d\n",RootPTR->Data);Insert2GlobalArray(&GA,RootPTR->Data);InOrderTraverse(RootPTR->RightNodePtr);}return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
11、PreOrderTraverse
(1)描述
前序遍历递归方法实现。
(2)定义
Status PreOrderTraverse(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}else{Insert2GlobalArray(&GA,RootPTR->Data);PreOrderTraverse(RootPTR->LeftNodePtr);PreOrderTraverse(RootPTR->RightNodePtr);}return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
12、PostOrderTraverse
(1)描述
后序遍历递归方法实现。
(2)定义
Status PostOrderTraverse(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}else{PostOrderTraverse(RootPTR->LeftNodePtr);PostOrderTraverse(RootPTR->RightNodePtr);Insert2GlobalArray(&GA,RootPTR->Data);}return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
九、LINUX环境测试
[gbase@czg2 Tree]$ make
gcc -Wall -g ../Log/Log.c BinaryTree.c main.c -o TestBinaryTree -I ../Log/[gbase@czg2 Tree]$ ./TestBinaryTree
2023-3--[Info]--Init Global Array : OK
2023-3--[Info]--Init Binary Tree : OK
2023-3--[Info]--New Binary Search Tree : OK
2023-3--[Info]--PreOrderTraverse : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
2023-3--[Info]--PreOrderTraverseNoRcs : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverseNoRcs : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverseNoRcs : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
上一篇:试除法求约数
下一篇:DM8:执行计划操作符说明
