0. 简介

最简作者在看PX4的相关内容，其中需要提取对yaw角的估计，所以针对性的对ECL EKF2中的EKF-GSF 偏航估计器进行学习。国内外相关的资料很少，这里主要基于《使用 IMU 和 GPS 进行偏航对准》这篇文章的内容，并结合PX4官网的内容，完成介绍。相关的代码在GIthub上，这里结合代码来阅读学习原作者的相关阐述。值得一提的是Github上有一位大佬提供了一套PX4 ECL EKF公式推导以及代码解析的内容

1. EKF-GSF 偏航估计器描述

该算法能在没有磁强计或外部偏航传感器的情况下运行，其目的是自动修正偏航误差引起的起飞后导航损失。EKF在内部运行一个附加的多假设滤波器，该滤波器使用状态为NE速度和偏航角的多个三态扩展卡尔曼滤波器（EKF）。然后使用高斯和滤波器（GSF）组合这些单独的偏航角估计。各个三态EKF使用IMU和GPS水平速度数据（加上可选的空速数据），并且不依赖于偏航角或磁力计测量的任何先验知识。

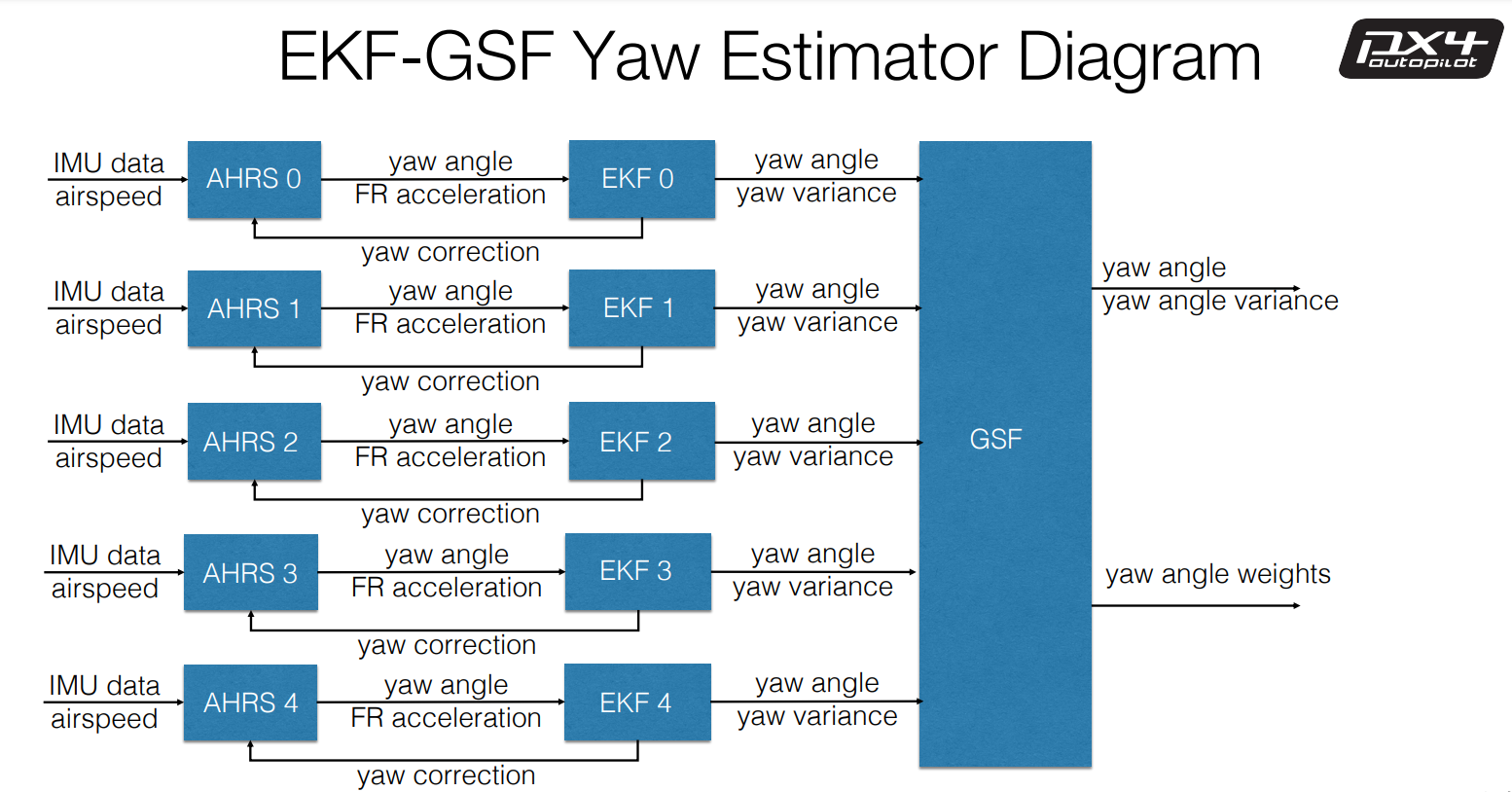
EKF-GSF 算法也是在 ECL EKF2 的 24 参数状态 EKF 之外又一个EKF实现，包括以下内容

• 使用互补滤波器的 5 组 AHRS 的解

  • 这些计算预测偏航角和向前、向右加速度。
  • 空速(测量或估计)用于固定翼飞行期间的向心加速度修正。

• 5 组 3 参数状态扩展卡尔曼滤波器

  • 状态为向北(N)、向东(E)速度和偏航角。
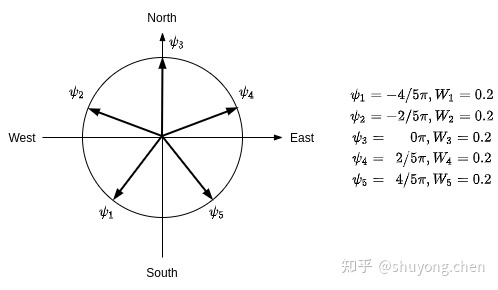
  • 偏航角估算开始时的角度间隔相等， [−4/5π−2/5π02/5π4/5π]\left[\begin{array}{ccccc} -4/5\pi & -2/5\pi & 0 & 2/5\pi & 4/5\pi\end{array}\right][−4/5π​−2/5π​0​2/5π​4/5π​] 。
  • GPS的向北(N)、向东(E)速度作为观测值。

• 高斯和滤波器(Gaussian Sum Filter)

  • 根据标准化 GPS 的向北(N)、向东(E)速度新息数值级别计算每个 EKF 的权重。总权重为 1 。
  • 输出偏航角 ψ\psiψ 估计值，这是单个 EKF 估计值的加权平均值。

GSF-EKF过程框图如下：

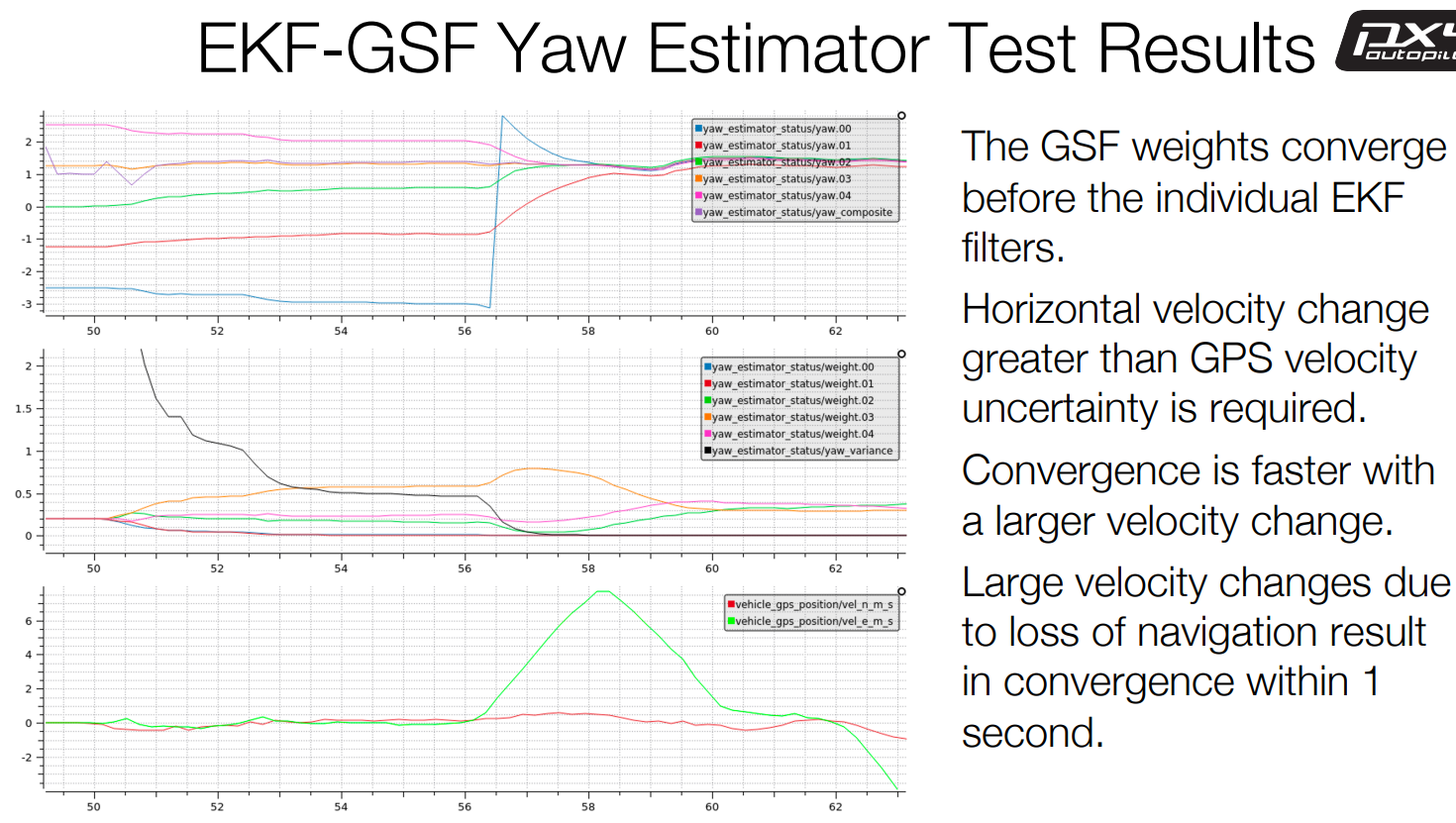
在我们拿到ulg文件后发现：

1. vehicle_angular_velocity大概45~50hz
2. vehicle_attitude大概20hz
   这就代表我们IMU的更新频率并不是很高，但是取得了比较好的收益
   

2. 偏航估计器的算法直觉

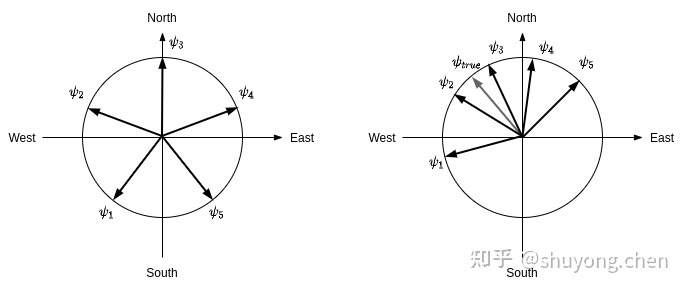
EKF-GSF 算法是一个很新奇也很有创意的算法。首先该算法一个假设就是偏航角由 xy 水平面的向北(N)、向东(E)的增量速度和绕 z 轴旋转的增量角度所驱动，所以偏航角的测量误差也和这 3 个值的测量噪声相关

ψerror∝(σΔVx2,σΔVy2,σΔψ2)\psi_{error}\propto\left(\sigma_{\Delta V_{x}}^{2},\sigma_{\Delta V_{y}}{2},\sigma_{\Delta\psi}{2}\right)ψerror​∝(σΔVx​2​,σΔVy​​2,σΔψ​2)

这 3 个值和 3 个噪声由 IMU 提供。于是我们可以在 xy 水平面上面预置 5 个偏航角 ψi,i∈1∼5\psi_{i},i\in1\sim5ψi​,i∈1∼5 ，每个偏航角由这 3 个值和 3 个噪声驱动演化，独立进行时间更新。在测量更新阶段，我们观测 GPS 提供的 xy 水平面的向北(N)、向东(E)的速度，因为残差的存在，这 5 个偏航角 ψi\psi_{i}ψi​ 会向真实的偏航角 ψtrue\psi_{true}ψtrue​ 聚拢，但是真实的偏航角 ψtrue\psi_{true}ψtrue​ 不可见。

不过我们可以通过高斯和的算法，计算这 5 个偏航角ψi\psi_{i}ψi​的权重并相加，得到距离真实的偏航角 ψtrue\psi_{true}ψtrue​ 最近的复合偏航角 ψGSF\psi_{GSF}ψGSF​ 。

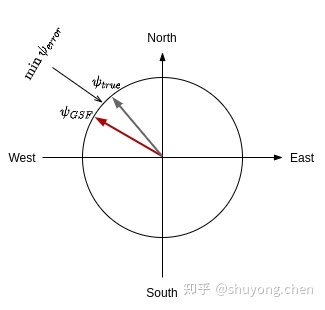
因此该算法就可以在没有磁强计的情况下估计偏航角，并且是水平速度变化越大，收敛越快。

3. 偏航估计器的初始化以及对齐

3.1 偏航估计器的初始化

初始化的关键在于在 xy 平面上预制 5 个偏航角，平均间隔，平均权重。其它初始化都是常规操作。

void EKFGSF_yaw::initialiseEKFGSF()//初始化EKF GSF
{_gsf_yaw = 0.0f;//初始化偏航角_ekf_gsf_vel_fuse_started = false;//初始化速度融合标志位_gsf_yaw_variance = _m_pi2 * _m_pi2;//初始化偏航角方差_model_weights.setAll(1.0f / (float)N_MODELS_EKFGSF);  // 所有的过滤器模型都以相同的权重开始memset(&_ekf_gsf, 0, sizeof(_ekf_gsf));//初始化所有的过滤器模型const float yaw_increment = 2.0f * _m_pi / (float)N_MODELS_EKFGSF;//偏航角增量for (uint8_t model_index = 0; model_index < N_MODELS_EKFGSF; model_index++) {//初始化每个过滤器模型,每个模型的偏航角都不一样,N_MODELS_EKFGSF为5// 在+-Pi之间均匀分配初始偏航角估计值_ekf_gsf[model_index].X(2) = -_m_pi + (0.5f * yaw_increment) + ((float)model_index * yaw_increment);// 取速度状态和与上次测量的相应方差_ekf_gsf[model_index].X(0) = _vel_NE(0);//速度东向_ekf_gsf[model_index].X(1) = _vel_NE(1);//速度北向_ekf_gsf[model_index].P(0,0) = sq(_vel_accuracy);//速度东向方差_ekf_gsf[model_index].P(1,1) = _ekf_gsf[model_index].P(0,0);//速度北向方差// 用半偏航间隔来表示偏航不确定性_ekf_gsf[model_index].P(2,2) = sq(0.5f * yaw_increment);//偏航角方差}
}

3.2 AHRS倾斜对齐

就是如何从增量速度计算旋转矩阵。旋转矩阵直接从加速度测量中构造，对于所有模型都是相同的，因此只需计算一次。其假设是：

偏航角为零 — 当速度融合开始时，每个模型的偏航角稍后对齐。
机体没有加速，因此所有测量的加速度都是由重力引起的。
用 Δt\Delta tΔt 表示传感器事件间隔时间。从 ECL EKF2 的主模块得到的加速度aI\boldsymbol{a}_{I}aI​ 计算得到增量速度 ΔVI\boldsymbol{\Delta V}_{I}ΔVI​

ΔVI=aI⋅Δt\boldsymbol{\Delta V}_{I}=\boldsymbol{a}_{I}\cdot\Delta tΔVI​=aI​⋅Δt

这是地球坐标系中的数据，需要转换到机体坐标系中并归一得到重力方向的单位向量

DB=−ΔVI/∥ΔVI∥\boldsymbol{D}_{B}=-\boldsymbol{\Delta V}_{I}/\left\Vert \boldsymbol{\Delta V}_{I}\right\VertDB​=−ΔVI​/∥ΔVI​∥

计算地球坐标系向北轴的单位向量，旋转为机体坐标系，与 DB\boldsymbol{D}_{B}DB​ 正交

NB=[100]−DB⋅([100]DB)NB=NB/∥NB∥\begin{array}{rl} \boldsymbol{N}_{B}&=\left[\begin{array}{c} 1\\ 0\\ 0 \end{array}\right]-\boldsymbol{D}_{B}\cdot\left(\left[\begin{array}{ccc} 1 & 0 & 0\end{array}\right]\boldsymbol{D}_{B}\right)\\\boldsymbol{N}_{B}&=\boldsymbol{N}_{B}/\left\Vert \boldsymbol{N}_{B}\right\Vert \end{array}NB​NB​​=​100​​−DB​⋅([1​0​0​]DB​)=NB​/∥NB​∥​

计算地球坐标系向东轴的单位向量，旋转为机体坐标系，与 DB\boldsymbol{D}_{B}DB​ 和 NB\boldsymbol{N}_{B}NB​ 正交

EB=DB×NB\boldsymbol{E}_{B}=\boldsymbol{D}_{B}\times\boldsymbol{N}_{B}EB​=DB​×NB​

从地球坐标系到机体坐标系的旋转矩阵中的每一列表示旋转到机体坐标系的相应地球坐标系单位向量的投影，例如 NB\boldsymbol{N}_{B}NB​ 将是第一列。我们需要从机体坐标系到地球坐标系的旋转矩阵，因此旋转到机体坐标系的地球坐标系单位向量被复制到相应的行中

[T]BN=[NBTEBTDBT]\left[T\right]_{B}^{N}=\left[\begin{array}{c} \boldsymbol{N}_{B}^{\mathrm{T}}\\ \boldsymbol{E}_{B}^{\mathrm{T}}\\ \boldsymbol{D}_{B}^{\mathrm{T}} \end{array}\right][T]BN​=​NBT​EBT​DBT​​​

倾斜对齐完成后可对每一个模型进行时间更新。

void EKFGSF_yaw::ahrsAlignTilt()//AHRS倾斜对齐
{// 旋转矩阵是直接从加速度测量中构建的，对于也是如此// 所有模型只需要计算一次假设是://   1)偏航角为零——当速度融合开始时，每个模型的偏航角稍后对齐。//   2)车辆没有加速，因此所有测量的加速度都是由重力引起的。// 计算地球框架下轴单位矢量旋转到身体框架,归一得到重力方向的单位向量const Vector3f down_in_bf = -_delta_vel.normalized();// 计算大地框架旋转到车身框架的北轴单位矢量，正交于`down_in_bf `const Vector3f i_vec_bf(1.0f,0.0f,0.0f);Vector3f north_in_bf = i_vec_bf - down_in_bf * (i_vec_bf.dot(down_in_bf));north_in_bf.normalize();// 计算旋转到车身框架的地轴东轴单位矢量，正交于“down_in_bf”和“north_in_bf”const Vector3f east_in_bf = down_in_bf % north_in_bf;// 从地球框架到地球框架的旋转矩阵中的每一列表示的投影// 对应的地球框架单位向量旋转到身体框架，例如'north_in_bf'将是第一列。// 我们需要从body框架到earth框架的旋转矩阵，以便earth框架单位向量旋转到body// 将帧复制到相应的行中。Dcmf R;R.setRow(0, north_in_bf);R.setRow(1, east_in_bf);R.setRow(2, down_in_bf);for (uint8_t model_index = 0; model_index < N_MODELS_EKFGSF; model_index++) {_ahrs_ekf_gsf[model_index].R = R;}
}

偏航角对齐完成后可对每一个模型进行测量更新。

3.3 AHRS预测

在每次时间更新前先从 IMU 数据生成姿态基准，即每一个模型的姿态矩阵 [T]BN\left[T\right]_{B}^{N}[T]BN​ 被 IMU 数据驱动往前旋转了一个角度。所用数据为 IMU 数据及真实空速(固定翼飞机)，并用加速度融合增益系数和陀螺仪偏差增益系数进行计算。最后计算得到一个校正后的增量角度，将其应用到姿态矩阵 [T]BN\left[T\right]_{B}^{N}[T]BN​ 就得到新的姿态矩阵。

void EKFGSF_yaw::ahrsPredict(const uint8_t model_index)
{// 对所选模型使用简单的互补滤波器生成姿态解const Vector3f ang_rate = _delta_ang / fmaxf(_delta_ang_dt, 0.001f) - _ahrs_ekf_gsf[model_index].gyro_bias;const Dcmf R_to_body = _ahrs_ekf_gsf[model_index].R.transpose();// 旋转矩阵转置const Vector3f gravity_direction_bf = R_to_body.col(2);// 重力方向// 使用加速度数据进行角速度修正，并在加速度幅度偏离1g时减少修正(减少车辆拾取和移动时的漂移)。在固定翼飞行，补偿向心加速度假设协调转弯和X轴向前Vector3f tilt_correction;if (_ahrs_accel_fusion_gain > 0.0f) {// 如果加速度融合增益大于0Vector3f accel = _ahrs_accel;// 加速度if (_true_airspeed > FLT_EPSILON) {// 如果向心加速度补偿的真实空速大于0// 假设X轴与空速向量对齐，计算车体框架向心加速度，使用车体速率与车体向心加速度向量补偿的真实空速的叉积const Vector3f centripetal_accel_bf = Vector3f(0.0f, _true_airspeed * ang_rate(2), - _true_airspeed * ang_rate(1));// 正确测量的向心加速度accel -= centripetal_accel_bf;}tilt_correction = (gravity_direction_bf % accel) * _ahrs_accel_fusion_gain / _ahrs_accel_norm;// 重力方向与加速度取余，乘以加速度融合增益除以加速度的模}// 陀螺偏差估计constexpr float gyro_bias_limit = 0.05f;const float spinRate = ang_rate.length();if (spinRate < 0.175f) {// 如果旋转速率小于0.175_ahrs_ekf_gsf[model_index].gyro_bias -= tilt_correction * (_gyro_bias_gain * _delta_ang_dt);// 陀螺偏差减去倾斜修正乘以陀螺偏差增益乘以增量角度时间_ahrs_ekf_gsf[model_index].gyro_bias = matrix::constrain(_ahrs_ekf_gsf[model_index].gyro_bias, -gyro_bias_limit, gyro_bias_limit);// 限制陀螺偏差}// 前一帧与当前帧的角度差const Vector3f delta_angle_corrected = _delta_ang + (tilt_correction - _ahrs_ekf_gsf[model_index].gyro_bias) * _delta_ang_dt;// 增量角度加上倾斜修正减去陀螺偏差乘以增量角度时间// 对旋转矩阵应用角度_ahrs_ekf_gsf[model_index].R = ahrsPredictRotMat(_ahrs_ekf_gsf[model_index].R, delta_angle_corrected);}

3.4 AHRS偏航角对齐

其算法是根据最新的偏航角 \psi 更新欧拉角向量，进而生成新的姿态矩阵 [T]BN\left[T\right]_{B}^{N}[T]BN​ 。在 24 参数 EKF 算法之外，在 EKF-GSF 算法中为每一个模型用增益系数法维护一个独立的姿态矩阵[T]BN\left[T\right]_{B}^{N}[T]BN​ ，用于后面的算法中。

void EKFGSF_yaw::ahrsAlignYaw()//AHRS偏航角对齐
{// 对齐每个模型的偏航角for (uint8_t model_index = 0; model_index < N_MODELS_EKFGSF; model_index++) {Dcmf& R = _ahrs_ekf_gsf[model_index].R;//获取ekf gsf的R,并传入const float yaw = wrap_pi(_ekf_gsf[model_index].X(2));//获取ekf gsf的yawR = updateYawInRotMat(yaw, R);//基于yaw角更新R_ahrs_ekf_gsf[model_index].aligned = true;//对齐标志位}
}

3.5 AHRS更新

同样的，在每次测量更新之后，需要对姿态矩阵 [T]BN\left[T\right]_{B}^{N}[T]BN​ 进行更新。因为增量偏航角 Δψ\Delta\psiΔψ 发生在 xy 平面上，所以利用偏航旋转矩阵的稀疏性可以对姿态矩阵 [T]BN\left[T\right]_{B}^{N}[T]BN​ 做优化更新。

	// 利用偏航角旋转矩阵的稀疏性，将偏航角的变化应用于AHRSconst float cosYaw = cosf(yawDelta);const float sinYaw = sinf(yawDelta);const float R_prev00 = _ahrs_ekf_gsf[model_index].R(0, 0);const float R_prev01 = _ahrs_ekf_gsf[model_index].R(0, 1);const float R_prev02 = _ahrs_ekf_gsf[model_index].R(0, 2);_ahrs_ekf_gsf[model_index].R(0, 0) = R_prev00 * cosYaw - _ahrs_ekf_gsf[model_index].R(1, 0) * sinYaw;//旋转矩阵R_ahrs_ekf_gsf[model_index].R(0, 1) = R_prev01 * cosYaw - _ahrs_ekf_gsf[model_index].R(1, 1) * sinYaw;_ahrs_ekf_gsf[model_index].R(0, 2) = R_prev02 * cosYaw - _ahrs_ekf_gsf[model_index].R(1, 2) * sinYaw;_ahrs_ekf_gsf[model_index].R(1, 0) = R_prev00 * sinYaw + _ahrs_ekf_gsf[model_index].R(1, 0) * cosYaw;_ahrs_ekf_gsf[model_index].R(1, 1) = R_prev01 * sinYaw + _ahrs_ekf_gsf[model_index].R(1, 1) * cosYaw;_ahrs_ekf_gsf[model_index].R(1, 2) = R_prev02 * sinYaw + _ahrs_ekf_gsf[model_index].R(1, 2) * cosYaw;

4. 偏航角预测方程

4.1 在预测中的变量意义

令 ψ\psiψ 表示机体坐标系相对于地球坐标系的偏航角(yaw)。

令 VNE\boldsymbol{V}_{NE}VNE​ 表示机体在世界坐标系中的向北(N)和向东(E)的速度，

VNE=[VNVE]\boldsymbol{V}_{NE}=\left[\begin{array}{c} V_{N}\\ V_{E} \end{array}\right]VNE​=[VN​VE​​]

令 Δψ\Delta\psiΔψ 表示 IMU 的 z 轴在机体轴上的增量角度测量值，即增量偏航角的测量值。

令 σΔψ2\sigma_{\Delta\psi}^{2}σΔψ2​ 表示 IMU 的 z 轴增量角度测量方差值。

令ΔVxy\boldsymbol{\Delta V}_{xy}ΔVxy​ 表示 IMU 的 x 轴和 y 轴在机体轴上的增量速度测量值

ΔVxy=[ΔVxΔVy]\boldsymbol{\Delta V}_{xy}=\left[\begin{array}{c} \Delta V_{x}\\ \Delta V_{y} \end{array}\right]ΔVxy​=[ΔVx​ΔVy​​]

令 σΔVxy2\boldsymbol{\sigma}_{\boldsymbol{\Delta V}xy}^{2}σΔVxy2​ 表示 IMU 的 x 轴和 y 轴增量速度测量方差

σΔVxy2=[σΔVx2σΔVy2]\boldsymbol{\sigma}_{\boldsymbol{\Delta V}xy}^{2}=\left[\begin{array}{c} \sigma_{\Delta V_{x}}^{2}\\ \sigma_{\Delta V_{y}}^{2} \end{array}\right]σΔVxy2​=[σΔVx​2​σΔVy​2​​]

…详情请参照古月居