蓝桥冲刺31天之317
在这个时代,我们总是在比较,觉得自己不够好
其实不必羡慕别人的闪光点
每个人都是属于自己的限量版
做你喜欢并且擅长的事,做到极致
自然会找到自己独一无二的价值
鸟不跟鱼比游泳,鱼不跟鸟比飞翔
你我各有所长
A:组队
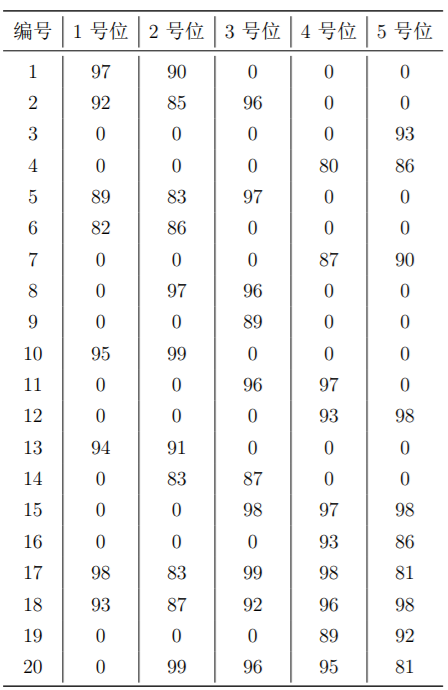
题目描述
作为篮球队教练,你需要从以下名单中选出 1 号位至 5 号位各一名球员,组成球队的首发阵容。
每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1 号位至 5 号位的评分之和最大可能是多少?
答案:
97+99+98+98+98(别问,看出来的,不会写代码)
B:不同子串
题目描述。
一个字符串的非空子串是指字符串中长度至少为 1 的连续的一段字符组成的串。例如,字符串 aaab 有非空子串 a, b, aa, ab, aaa, aab, aaab,一共 7 个。注意在计算时,只算本质不同的串的个数。
请问,字符串 0100110001010001有多少个不同的非空子串?
思路解析:
通过HashSet去存储每一种不同的子串,最终输出HashSet的长度即可(不会的朋友可以去搜一下对应知识点)
参考代码:
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;public class Main {public static void main(String[] args) {String s = "0100110001010001";Set set = new HashSet<>();for (int i = 0; i < s.length(); i++) {for (int j = i + 1; j <= s.length(); j++) {String str = s.substring(i,j);set.add(str);}}System.out.println(set.size());}
}
C:等差数列
题目描述
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一 部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有几项?
输入描述
输入的第一行包含一个整数 NN。
第二行包含 NN个整数 A1,A2,⋅⋅⋅,AN。(注意 A1∼ AN 并不一定是按等差数列中的顺序给出)
其中,2≤N≤10^5,0≤Ai≤10^9。
输出描述
输出一个整数表示答案。
输入输出样例
5 2 6 4 10 2010样例说明: 包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、 18、20。
题解思路:
我们将输入的数据排序,提取出每一个数与前一个数的差值,因为等差数列的话任意两数之间的差值相同,我们只需要去判断提取出来的n-1个差值中的最大公因数即可
参考代码:
import java.util.Scanner;
import java.util.Arrays;
public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();//个数long []arr=new long[n];for (int i=0;iD:波动数列
题目描述
观察这个数列:
1 3 0 2 −1 1 −2 ⋯
这个数列中后一项总是比前一项增加 2 或者减少 3。
栋栋对这种数列很好奇,他想知道长度为 n 和为 s 而且后一项总是比前一项增加 aa 或者减少 bb 的整数数列可能有多少种呢?
输入描述
输入的第一行包含四个整数 n,s,a,b,含义如前面说述。
其中,1≤n≤1000,−10^9≤s≤10^9,1≤a,b≤10^6。
输出描述
输出一行,包含一个整数,表示满足条件的方案数。由于这个数很大,请输出方案数除以 100000007的余数。
输入输出样例
4 10 2 32样例说明:这两个数列分别是 2 4 1 3 和 7 4 1 -2。
题解思路:
因为x为整数,因此需要满足下述条件:
因为可以取负数,因此在判断的时候,需要取该值的正整数,公式为:
(a%b+b)%b
接下来就是一个背包问题,从
开始往
计算,因为不知道是+2还是-3
因此每次得到结果为arr[i][j] = (arr[i - 1][((j-a*i)%n+n)%n] + arr[i - 1][((j+b*i)%n+n)%n])
其中i表示存入的第i个数,j表示前i个数按照上述公式下模为j的方案数
arr[i-1]指上一个数放入后j-a*i,表示当前arr[i][j]是通过上一个放入数以后,+2获得模为j
j+b*i,表示当前arr[i][j]是通过上一个放入数以后,-3获得模为j
因此arr[i][j]=(arr[i - 1][((j-a*i)%n+n)%n] + arr[i - 1][((j+b*i)%n+n)%n])%100000007
最终我们放入了n个数,实际上方案数就是:arr[n-1][(S%n+n)%n]
参考代码:
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int s = sc.nextInt();int a = sc.nextInt();int b = sc.nextInt();int [][]arr=new int[n+1][n+1];arr[0][0] = 1;for (int i = 1; i < n; i++) {//放入for (int j = 0; j < n; j++) {//遍历模值方案数arr[i][j] = (arr[i - 1][((j-a*i)%n+n)%n] + arr[i - 1][((j+b*i)%n+n)%n]) % 100000007;}}System.out.print(arr[n - 1][(s%n+n)%n]);}
}