1.前序遍历

1.1前序遍历概念

[前序遍历](前序遍历_百度百科 (baidu.com))（VLR）， [1] 是二叉树遍历的一种，也叫做先根遍历、先序遍历、前序周游，可记做根左右。前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。

数学表达式形式：当对一棵数学表达式树进行中序，前序和后序遍历时，就分别得到表达式的中缀、前缀和后缀形式。

在后缀（postfix）表达式中，每个操作符跟在操作数之后，操作数按从左到右的顺序出现。在前缀（prefix）表达式中，操作符位于操作数之前。在前缀和后缀表达式中不会存在歧义。

因此，在前缀和后缀表达式中都不必采用括号或优先级。从左到右或从右到左扫描表达式并采用操作数栈，可以很容易确定操作数和操作符的关系。若在扫描中遇到一个操作数，把它压入堆栈，若遇到一个操作符，则将其与栈顶的操作数相匹配。把这些操作数推出栈，由操作符执行相应的计算，并将所得结果作为操作数压入堆栈。

1.2前序遍历习题

二叉树的前序遍历。 OJ链接

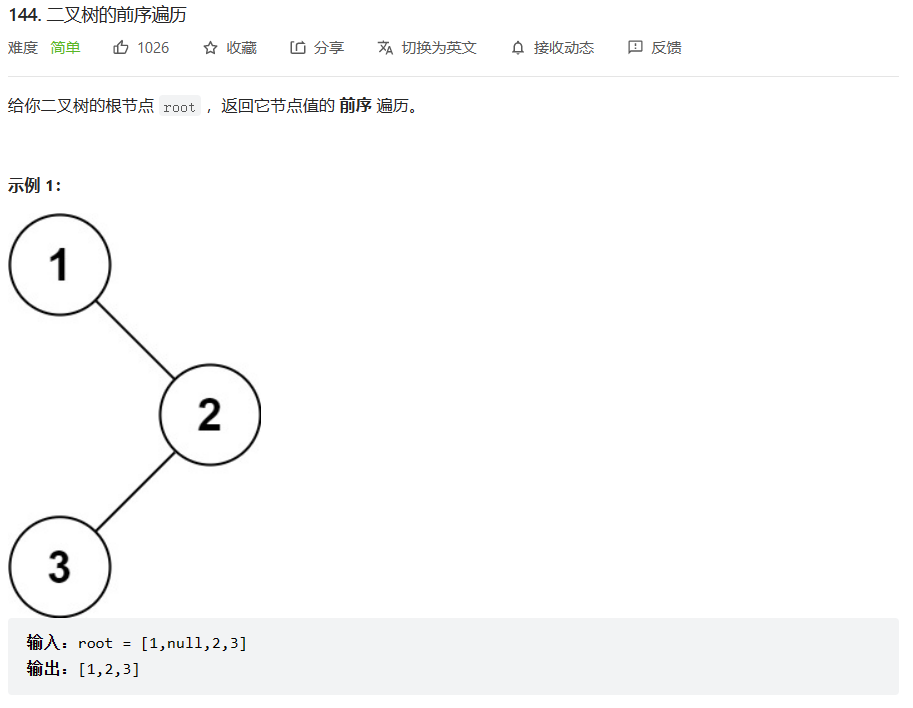
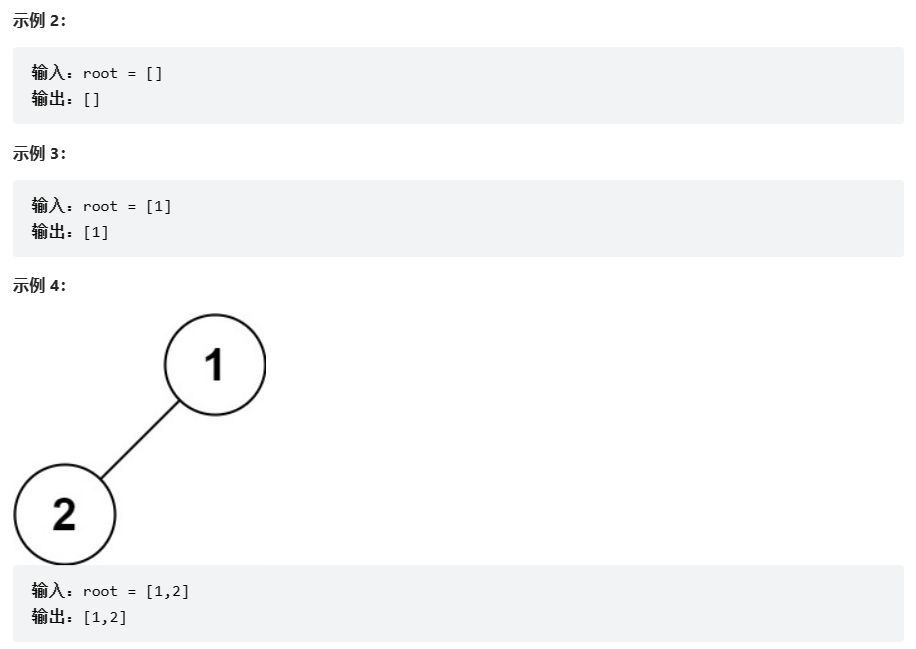
解法一(遍历思路：只new一个list，然后直接递归走完每一次，直接返回list)：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {List list = new ArrayList<>();public List preorderTraversal(TreeNode root) {if (root == null) {return list;}list.add(root.val);preorderTraversal(root.left);preorderTraversal(root.right);return list;}
}

解法二(子问题思路：每次都new一个新的list 再每一次递归时将他们直接存入list中)：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List preorderTraversal(TreeNode root) {List list = new ArrayList<>();if (root == null) {return list;}list.add(root.val);List leftTree = preorderTraversal(root.left);list.addAll(leftTree);List rightTree = preorderTraversal(root.right);list.addAll(rightTree);return list;}
}

思路：利用循环递归的方法来解决前序遍历法。

2.中序遍历

2.1中序遍历概念

[中序遍历](中序遍历_百度百科 (baidu.com))是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

数学表达式形式：当对一棵数学表达式树进行中序，前序和后序遍历时，就分别得到表达式的中缀、前缀和后缀形式。中缀（infix）形式即平时所书写的数学表达式形式，在这种形式中，每个二元操作符（也就是有两个操作数的操作符）出现在左操作数之后，右操作数之前。在使用中缀形式时，可能会产生一些歧义。例如，x+y ×z可以理解为(x+y) ×z或x+ (y ×z)。为了避免这种歧义，可对操作符赋于优先级并采用优先级规则来分析中缀表达式。在完全括号化的中缀表达式中，每个操作符和相应的操作数都用一对括号括起来。更甚者把操作符的每个操作数也都用一对括号括起来。如( (x) + (y) )，( (x) + ( (y) * (z) ) )和( ( (x) + (y) ) * ( (y) + (z) ) ) * (w)。

2.2中序遍历习题

二叉树中序遍历。OJ链接

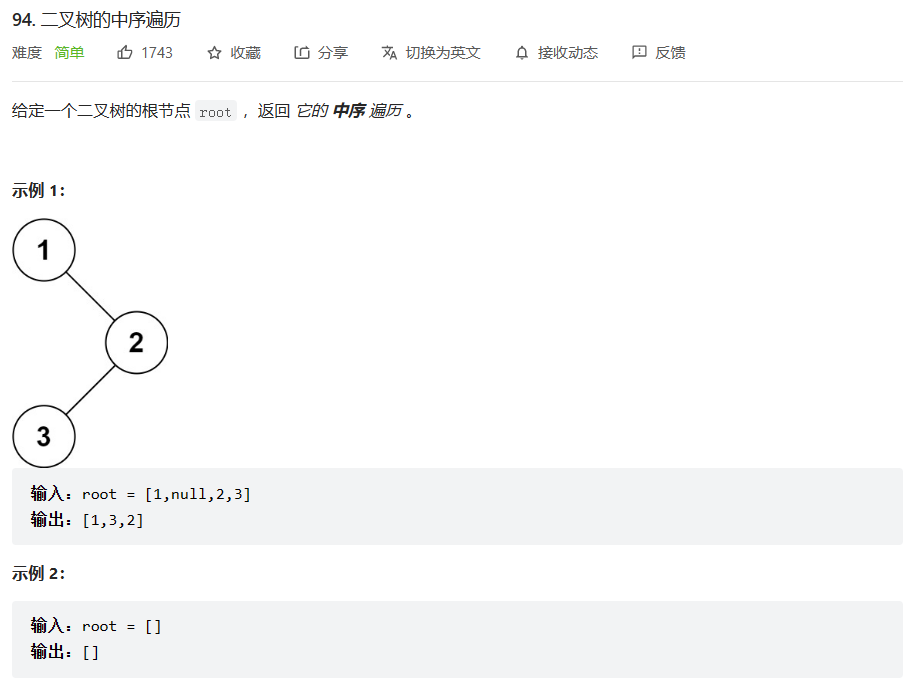
/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List inorderTraversal(TreeNode root) {List list = new ArrayList<>();if (root == null) {return list;}List leftTree = inorderTraversal(root.left);list.addAll(leftTree);list.add(root.val);List rightTree = inorderTraversal(root.right);list.addAll(rightTree);return list;}
}

思路：子问题思路：每次都new一个新的list 再每一次递归时将他们直接存入list中，利用循环递归的方法来解决前序遍历法。

3.后续遍历

3.1后序遍历概念

后序遍历（LRD）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中，先左后右再根，即首先遍历左子树，然后遍历右子树，最后访问根结点。

3.2后序遍历习题

二叉树的后序遍历。OJ链接

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List postorderTraversal(TreeNode root) {List list = new ArrayList<>();if (root == null) {return list;}List leftTree = postorderTraversal(root.left);list.addAll(leftTree);List rightTree = postorderTraversal(root.right);list.addAll(rightTree);list.add(root.val);return list;}
}

思路：子问题思路：每次都new一个新的list 再每一次递归时将他们直接存入list中，利用循环递归的方法来解决前序遍历法。