将节点映射成D维向量主要有以下几种方法：

        ①人工特征工程：节点重要度、集群系数、Graphlet等

        ②图表示学习：通过随机游走构造自监督学习来实现，如DeepWalk，Node2Vec等

        ③矩阵分解

        ④深度学习：图神经网络

一、图嵌入

        传统图机器学习需要使用人为的特征工程来实现图到D维向量的转换。而图表示学习是有计算机自动学习特征将各模态输入转换为向量，这个过程不需要人工干预。

         d维向量有如下特点：

                低维：向量的维度远小于节点数

                连续：每个元素都是实数

                稠密：每个元素都不为0（区别于热编码）

        嵌入向量包含网络的连接信息，且能用于下游任务。

二、基本框架

        1.编码器

                输入一个节点，经过处理后输出其对应的d维向量。

        2.解码器

                将编码器得到的向量进行点积，得到其余弦相似度（标量，可以反映节点的相似度）

        ！！！需注意的是编码器和解码器的结构是可以更换的，不一定是点积，得到的也不一定是余弦相似度。

        框架迭代优化的方向是：使得图中相似节点的向量数量积大，不相似节点的向量数量积小。

三、常见的编码器

        1.浅编码器

                实质上是人为将所有节点的d维向量写入一个矩阵中，将此矩阵与一个热编码(one-hot)向量相乘即可得到嵌入向量，记作：；其中矩阵的参数为可学习参数。

        2.随机游走

                从节点出发，生成一个随机游走序列，求其经过节点的概率，记作：。

                可以通过softmax激活函数计算：或sigmoid计算：

                ①Deepwalk

                        1.采样得到若干随机游走序列，计算条件概率

                        2.迭代优化每个节点的d维向量，使得序列中共现节点向量数量积大，不共现节点向量数量积小。

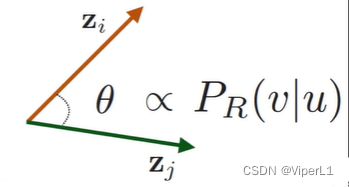
        似然目标函数：，其中为从节点出发的随机游走序列，游走策略为。

        损失函数：，其中概率由softmax计算

         负采样：可以将，近似为，此式中的 k 为负样本个数。k一般取5-20，且统一个游走序列中的节点不应被采样为“负样本”。

                Node2vec

                        其余步骤和Deepwalk一致，但是可以通过设置超参数来规定随机游走的偏向性：BFS--宽度优先--局部探索；DFS--深度优先--全局探索