目录

• [简单]101. 对称二叉树
• [简单]102. 二叉树的层序遍历
• [简单]111. 二叉树的最小深度
• [简单]110. 平衡二叉树
• [中等]200. 岛屿数量

[简单]101. 对称二叉树

• 原题链接
• 题解
  比较基础的递归思想，按照对称点的方式递归，递归函数中，第一个参数是左半边的点，第二个参数是右半边的对称点，因此，进入子节点递归的时候，左半边的点进入其左孩子时，右半边的对称点要进入其右孩子，左半边的点进入其右孩子时，右半边的对称点要进入其左孩子。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;return recursion(root->left,root->right);}bool recursion(TreeNode* left, TreeNode* right){if(left == nullptr && right == nullptr) return true;else if(left == nullptr || right == nullptr) return false;if(left->val != right->val) return false;if(!recursion(left->left,right->right)) return false;if(!recursion(left->right,right->left)) return false;return true;}
};

[简单]102. 二叉树的层序遍历

• 原题链接
• 题解
  经典的借助队列进行层序遍历的思路，在while循环中再加一层for循环，来区别每一层的节点即可

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector> levelOrder(TreeNode* root) {queue q;vector> ans;vector nums;if(root == nullptr) return ans;q.push(root); while(!q.empty()){int n = q.size();nums.clear();for(int i=0;iTreeNode* node = q.front();q.pop();nums.push_back(node->val);if(node->left) q.push(node->left);if(node->right) q.push(node->right);}ans.push_back(nums);}return ans;}
};

[简单]111. 二叉树的最小深度

• 原题链接
• 题解
  层序遍历，一旦有哪一层节点是叶子节点，直接return即可

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://广度优先遍历，一旦找到叶子节点，返回深度并停止遍历int minDepth(TreeNode* root) {if(root == nullptr) return 0;queue q;q.push(root); int deep = 0;while(!q.empty()){int n = q.size();deep++;for(int i=0;iTreeNode* node = q.front();q.pop();if(node->left) q.push(node->left);if(node->right) q.push(node->right);if(node->left == nullptr && node->right == nullptr){return deep;}}}return deep;}
};

[简单]110. 平衡二叉树

• 原题链接
• 题解
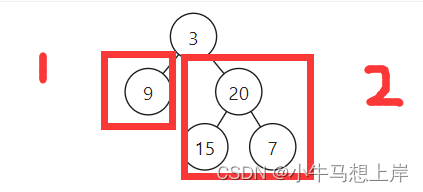
  每次递归先获取左右子树的高度，分别为leftDepth与rightDepth，二者的差值可在[-1,0,1]中则表示以当前节点为根的子树是平衡的，如果不平衡就返回-1，一旦收到左右子树有返回-1，则当前节点也直接返回-1，保证将不有序的情况层层向上传递。

ps:（这题其实还简化了，在数构里面一半平衡树是基于有序树的基础上保证平衡，这种情况需要多判断一下各个节点是否满足有序树）。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isBalanced(TreeNode* root) {if(root == nullptr) return true;if(dfs(root) < 0) return false;return true;}int dfs(TreeNode* p){if(p == nullptr) return 0;if(!p->left && !p->right){return 1;}int leftDepth = 0;int rightDepth = 0;if(p->left) {leftDepth = dfs(p->left);if(leftDepth < 0) return -1;}if(p->right) {rightDepth = dfs(p->right);if(rightDepth < 0) return -1;}int diff = leftDepth-rightDepth;if(diff >= -1 && diff <= 1){return max(leftDepth,rightDepth) + 1;}return -1;}
};

[中等]200. 岛屿数量

• 原题链接
• 题解
  比较基础的多次深度优先遍历的题，对一个值为1的点，进入递归将其所有通过上下左右可到达的1标记为0，可以形象为用海水覆盖，这样下次就不会再遍历到，整个岛屿被覆盖后，就回到循环去找下一个岛屿。

class Solution {
public:int numIslands(vector>& grid) {int count = 0;for(int i=0;ifor(int j=0;jif(grid[i][j] == '1'){count++;dfs(grid,i,j);}}}return count;}void dfs(vector>& grid,int i,int j){cout << i << " " << j << endl; grid[i][j] = '0';//先覆盖当前点，之后便不会再扫描到他//向左检查if(j>0 && grid[i][j-1] == '1') dfs(grid,i,j-1);//向右检查if(j0 && grid[i-1][j] == '1') dfs(grid,i-1,j);//向下检查if(i