除了我们熟知的miou指标外，Dice，F1-score这2个指标也是分割问题中常用的指标。

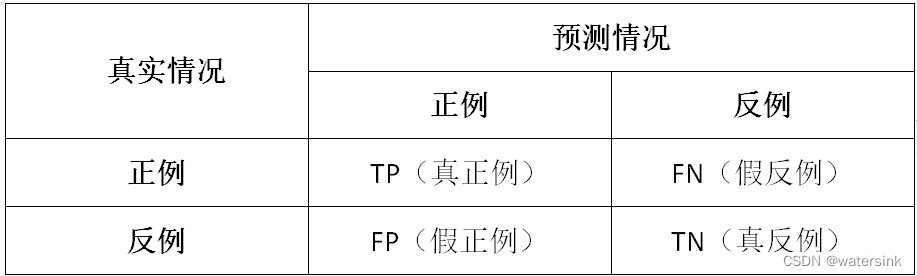
P(Precision) = TP/(TP + FP);

R(Recall) = TP/(TP + FN);

IoU = TP/(TP + FP + FN)

DICE (dice coefficient) = 2*TP/(FP + FN + 2 * TP)=2*IoU/(IoU+1)

F1-score = (2*P*R)/(P + R)=2*TP/(FP + FN + 2 * TP)=DICE

按照公式来看，其实Dice==F1-score

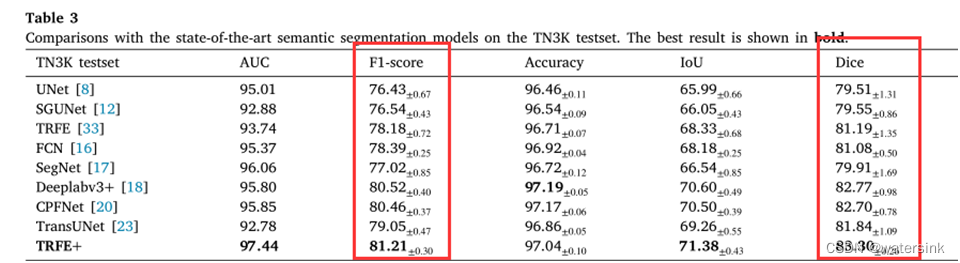
但是我看论文里面虽然提供的公式是我上面贴的公式，但是他们的两个数值完全不一样，甚至还相差较大。

比如：这篇论文提供了权重和代码，我测出来的两个数值也是一样的，而且代码里面的计算公式和上面贴的公式一样，但是论文中给出来的结果就不一样了。

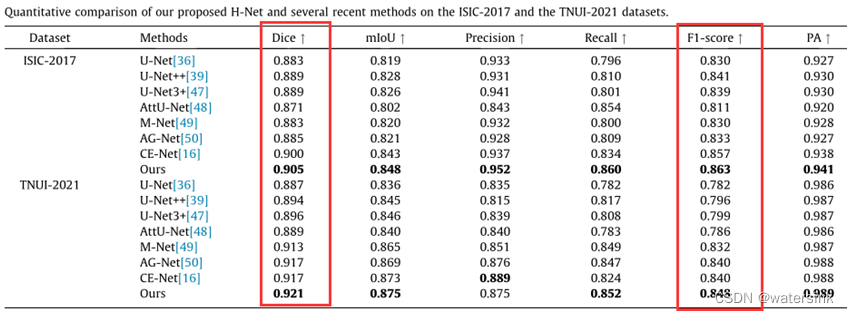
 还有这篇，这篇没有权重但是论文里写了公式 

那么这个是怎么造成的呢?

其实这里的dice准确的说叫soft dice，出自论文V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation，

Fbeta_score=(1 + beta2)*TP/[ beta2 *(TP+FN)+(TP+FP)] = (1 + beta2)* (true * pred) / [beta2 *true + pred]

F1_score=2*TP/[(TP+FN)+(TP+FP)] = 2* (true * pred) / [true + pred]

Dice = 2* (true * pred_score) / [true*true + pred_score* pred_score]

两个公式的区别，就是Dice使用的不是预测的结果pred，而是预测的结果的得分pred_score，并且做了平方操作。

这样最终算下来，就会得到Dice>F1_score

实现代码如下，github链接GitHub - miaotianyi/pytorch-confusion-matrix: Differentiable precision, recall, F-beta score, F1 score, and dice loss for input tensors of real-valued probabilities

def f_beta(y_true, y_pred, reduce_axes, beta=1., epsilon=1e-6):"""Differentiable F-beta scoreF_beta = (1 + beta^2) * TP / [beta^2 * (TP + FN) + (TP + FP)]= (1 + beta^2) (true * pred) / [beta^2 * true + pred]Using this formula, we don't have to use precision and recall.F1 score is an example of F-beta score with beta=1."""beta2 = beta ** 2   # beta squarednumerator = (1 + beta2) * (y_true * y_pred).sum(reduce_axes)denominator = beta2 * y_true.sum(reduce_axes) + y_pred.sum(reduce_axes)denominator = denominator.clamp(min=epsilon)return numerator / denominatordef dice(y_true, y_pred, reduce_axes, beta=1., epsilon=1e-6):"""Compute soft dice coefficient according to V-Net paper.(https://arxiv.org/abs/1606.04797)Unlike F-beta score, dice uses squared probabilitiesinstead of probabilities themselves for denominator.Due to the squared entries, gradients will be y_true and y_pred instead of 1."""beta2 = beta ** 2   # beta squarednumerator = (1 + beta2) * (y_true * y_pred).sum(reduce_axes)denominator = beta2 * y_true.square().sum(reduce_axes) + y_pred.square().sum(reduce_axes)denominator = denominator.clamp(min=epsilon)return numerator / denominator