下面答案仅供参考！

1．令文法G为:

       E→E+T∣T

       T→T*F∣F

       F→(E)∣i

证明E+T*F是它的一个句型,指出这个句型的所有短语,直接短语和句柄。

2．考虑下面的表格结构文法G2:

       S→a∣∧∣(T)

       T→T，S∣S

(1）给出( a，(a，a))和(((a，a)，Λ，(a))，a)的最左和最右推导。

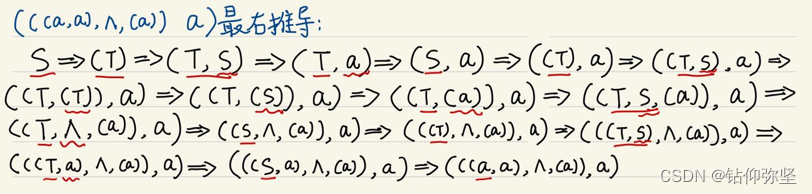
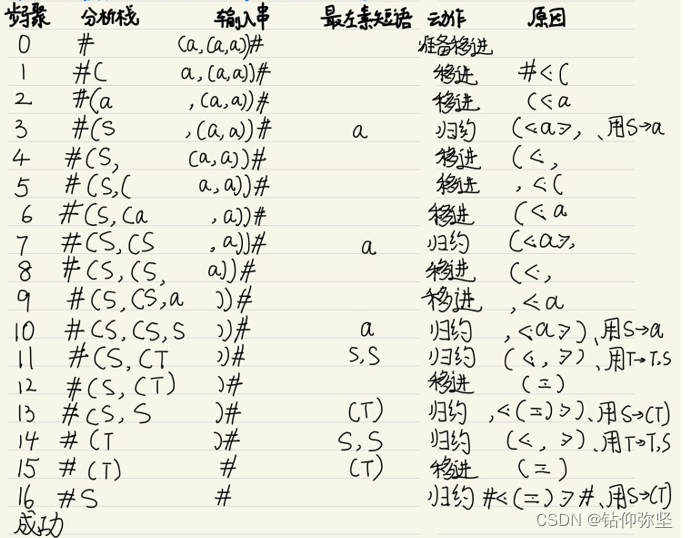
(2）指出(((a，a)，Λ，(a))，a)的规范归约及每一步的句柄。根据这个规范归约,给出“移进-归约”的过程,并给出它的语法树自下而上的构造过程。
 

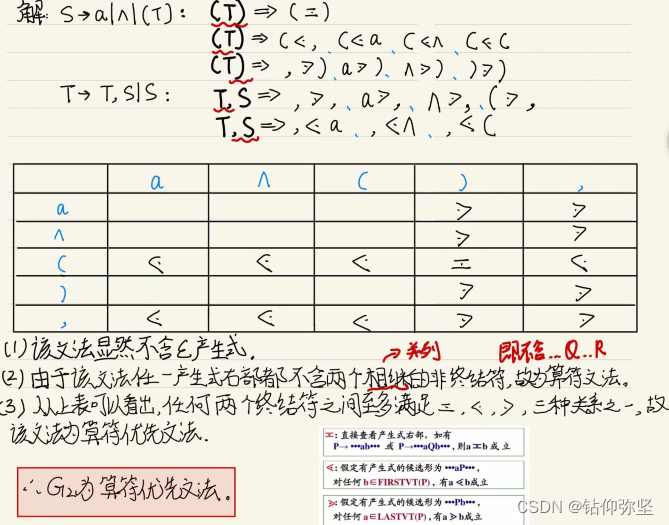
 3.(1)计算练习2文法的FIRSTVT和LASTVT。

(2)计算的优先关系。G是一个算符优先文法吗?

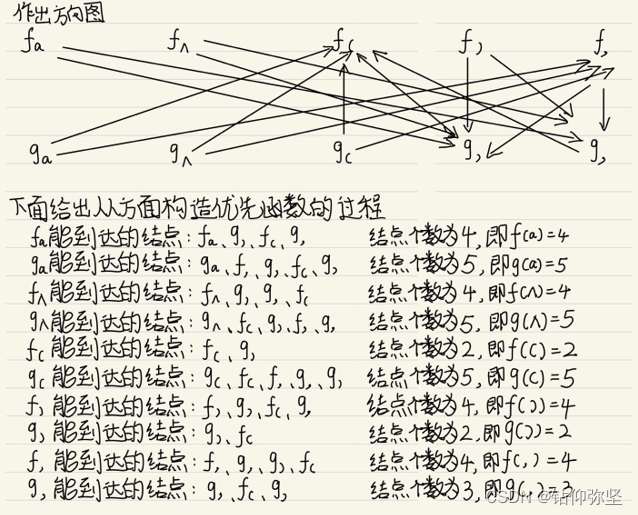
(3）计算的优先函数。

(4）给出输入串(a，(a，a))的算符优先分析过程。

4、存在一种称为简单优先的自下而上分析法，这种分析法不会把错误句子当作为正确句子。一个文法G，如果它不含ε-产生式，也不含任何右部相同的不同产生式，并且它的任何符号对（X，Y）——X和Y为终结符或非终结符——顶多存在下述三种关系=、<、>之一，则称这个文法G是一个简单优先文法。这三种关系的定义是：

 (1）构造文法G2的简单优先分析表,辨明它是否为一个简单优先文法?

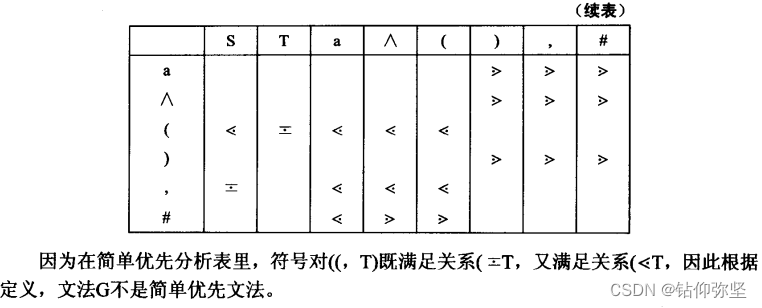
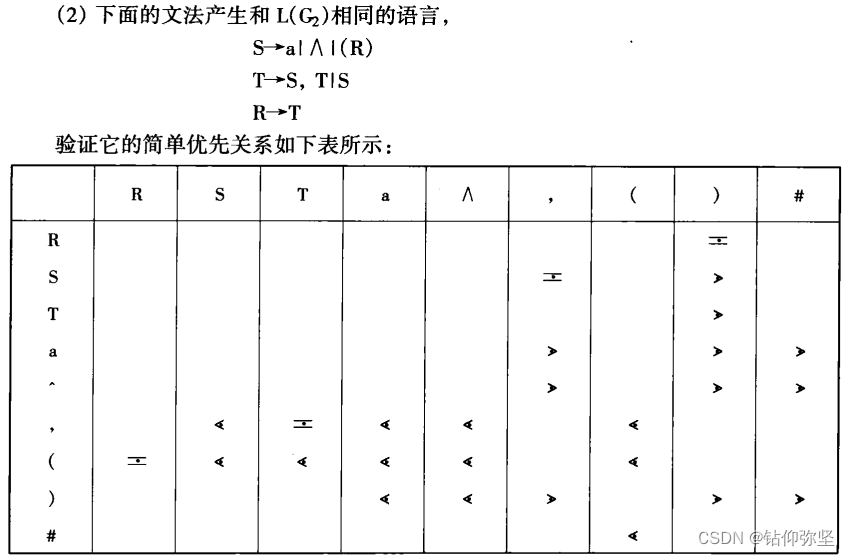
    由于简单优先文法定义了文法的所有终结符与非终结符的优先关系，为此，我们 对文法的每个非终结符构造两个集合，首符集FIRST和尾符集LAST(LAST的定义与FIRST 类似）。于是有： 

然后按照简单优先文法的优先关系来验证，可知题中给出的简单优先关系表是正确的。

(3) 按上面的简单优先表构造优先函数。

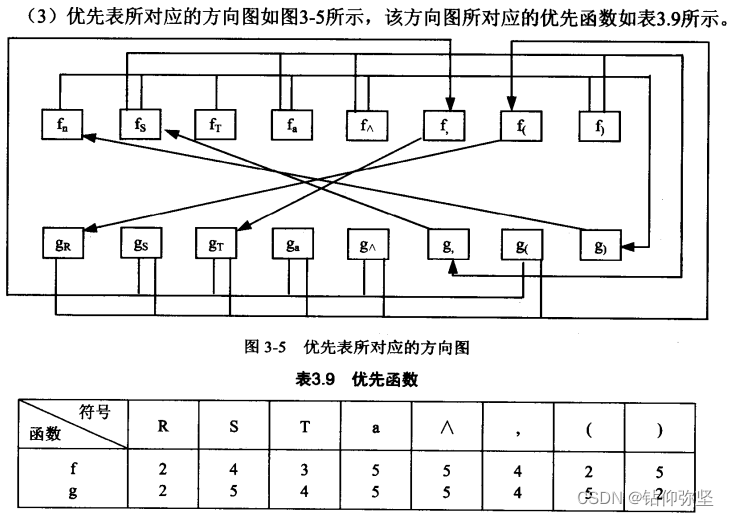
 (4)证明简单优先文法是无二义的。进一步说，简单优先文法的任何句型X1 X2...Xn的句柄是满足条件

 (5)构造简单优先分析器。

5、考虑文法：

       S→AS︱b

       A→SA︱a

（1）列出这个文法的所有LR(0)项目。

（2）构造这个文法的LR(0)项目集规范族及识别活前缀的DFA。

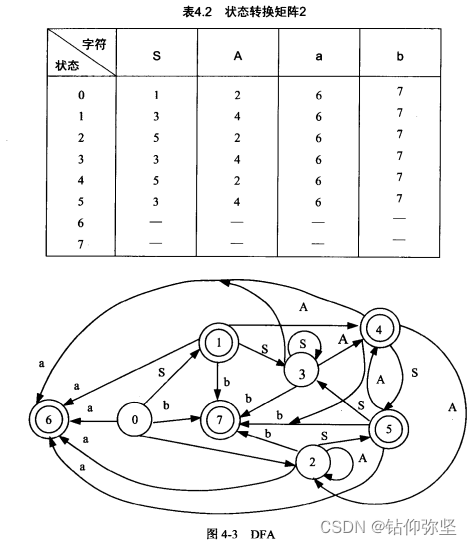
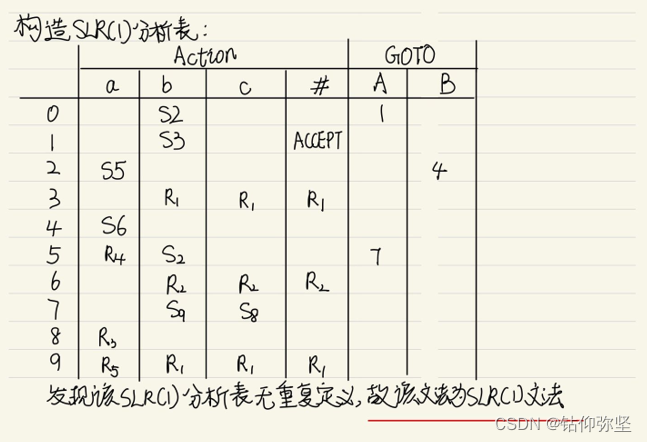
 （3）这个文法是SLR的吗？若是，构造出它的SLR分析表。

（4）这个文法是LALR或LR(1)的吗？

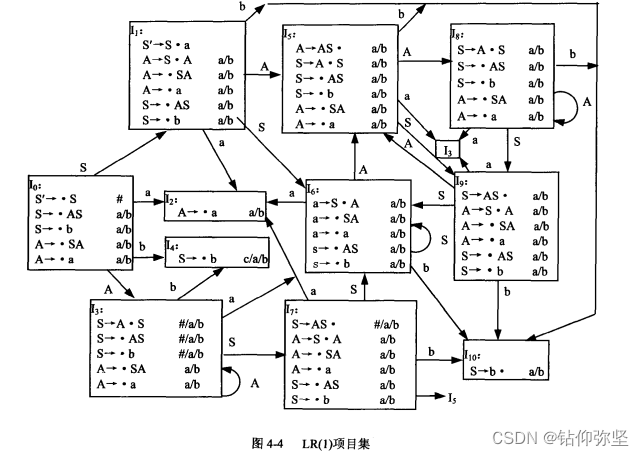
6、下面是一个描述∑={a，b}上的正规式的LALR文法（实际上也是SLR文法），只不过用‘+’代替‘∣’，用^代替ε（空字）。

       E→E+T∣T

       T→TF∣F

       F→F*∣(E)∣a∣b∣∧

       构造这个文法的LALR项目集和分析表。

      由于LALR项目集族不存在“移进-归约”冲突的集合，因此可按这个集族构造分析表。分析表如表4.3所示。

7、证明下面文法是SLR(1)但不是LR(0)的。

       S→A

       A→Ab∣bBa

       B→aAc∣a∣aAb

8、证明下面的文法是LL(1)的但不是SLR(1)的。

       S→AaAb∣BbBa

       A→ε

       B→ε

证明：

因为FIRST(AaAb)={a}，FIRST(BbBa)={b}

FIRST(AaAb)∩FIRST(BbBa)=Ø

所以该文法是LL(1)的。

求该文法的LR(0)项目集规范族如下：

       I0={S’→·S，S→·AaAb，S→·BbBa，A→·，B→·}

       I1={S→S·}

       I2={S→A·aAb}

       I3={S→B·bBa}

       I4={S→Aa·Ab，A→·}

       I5={S→Bb·Ba，B→·}

       I6={S→AaA·b}

       I7={S→BbB·a}

       I8={S→AaAb·}

       I9={S→BbBa·}

       考虑I0：FOLLOW(A)=FOLLOW(B)={a，b}

       A→·和B→·的冲突无法消解，所以该文法不是SLR(1)的。

9、证明下面文法是LALR(1)但不是SLR(1)的。

       S→Aa∣bAc∣Bc∣bBa

       A→d

（这题是不是应该把B改成d？贴一个另外一道题的解法）

设已给文法

(1)G1［S］：

S→Aa|bAc|dc|bda

A→d

(2)G2［S］：

S→Aa|bAc|Bc|bBa

A→d

B→d

试证明： G1是LALR(1)文法但不是SLR(1)文法；G2是LR(1)文法但不是LALR(1)文法。

证明G1：

构造LR(1)自动机（没有需要合并的状态）：

没有状态存在冲突，因而是LALR(1)文法.

构造LR(0)自动机：

在状态I6，由于’a’∈FOLLOW(A)，因而对于SLR(1)分析而言，存在移进-归约，所以这一文法不是SLR(1)文法.

证明G2：

1、 构造该文法的 LR(1) 语法分析表

构造该文法的增广文法

S'->S

S->Aa

S->bAc

S->Bc

S->bBa

A->d

B->d

1）构造该增广文法的 LR(1) 项集族如下

I0 S'->.S,$ S->.Aa,$ S->.bAc,$ S->.Bc,$ S->.bBa,$ A->.d,a B->.d,c	I1 S'->S.,$	I2 S->A.a,$	I6 S->Aa.,$	I10 S->Bc.,$	I12 S->bBa.,$
	I3 S->b.Ac,$ S->b.Ba,$ A->.d,c B->.d,a	I4 S->B.c,$	I7 S->bA.c.,$
					I9 A->d.,c B->d.,a
		I5 A->d.,a B->d.,c	I8 S->bB.a.,$	I11 S->bAc.,$

2）项集合并：没有可以合并的项集

3）GOTO函数

GOTO（I0，S）=I1 GOTO（I0 ，A）=I2 GOTO（I0 ，b）=I3 GOTO（I0 ，B）=I4 GOTO（I0 ，d）=I5 GOTO（I1,$）=acc GOTO（I2 ，a）=I6 GOTO（I3 ，A）=I7 GOTO（I3 ， B）=I8 GOTO（I3 ，d）=I9 GOTO（I4， c）=I10 GOTO（I7 ，c）=I11 GOTO（I8 ， a）=I12

4）构造 LR（1） 分析表如下

状态	ACTION					GOTO
	a	b	c	d	$	S	A	B
0		S3		S5		1	2	4
1					acc
2	S6
3				S9			7	8
4			S10
5	R5		R6
6					R1
7			S11
8	S12
9	R6		R5
10					R3
11					R2
12					R4

可见该分析表中不存在二义性的条目，故该文法是 LR(1) 文法2、 构造该文法的 LALR(1) 语法分析表①合并 LR(1) 项集族

I5 和 I9 可以合并为 I59

I59 A->d.,a/c B->d.,c/c

②构造 LALR(1) 语法分析表如下

状态	ACTION					GOTO
	a	b	c	d	$	S	A	B
0		S3		S59		1	2	4
1					acc
2	S6
3				S9			7	8
4			S9
59	R5|R6		R6|R6
6					R1
7			S10
8	S11
9					R3
10					R2
11					R4

可见该语法分析表中存在有二义性的条目，故该文法不是LALR（1）文法

10、如果我们用下面的二义文法产生正规式E→E+E∣EE∣E*∣(E) ∣a∣b∣∧

（1）给出解决二义性的YACC说明，按照这个说明能正确的分析正规式。

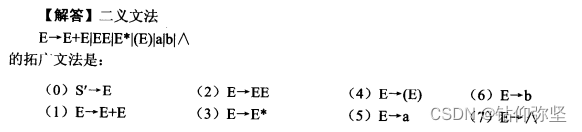
YACC接受用户提供的文法（可能是二义的）和算符优先级、结合性质等附加信 息，自动产生这个文法的LALR分析表。对于二义文法，需要相应的辅助信息。YACC解决 冲突性动作的方法是赋予每个终结符和产生式以一定的优先级，按优先级解决冲突。下面给出解决这个文法二义性的YACC说明。

YACC解决“归约-归约”冲突的原则是：优先级按箭头方向由高到低。故上述YACC 说明就可以正确地分析正规式。 

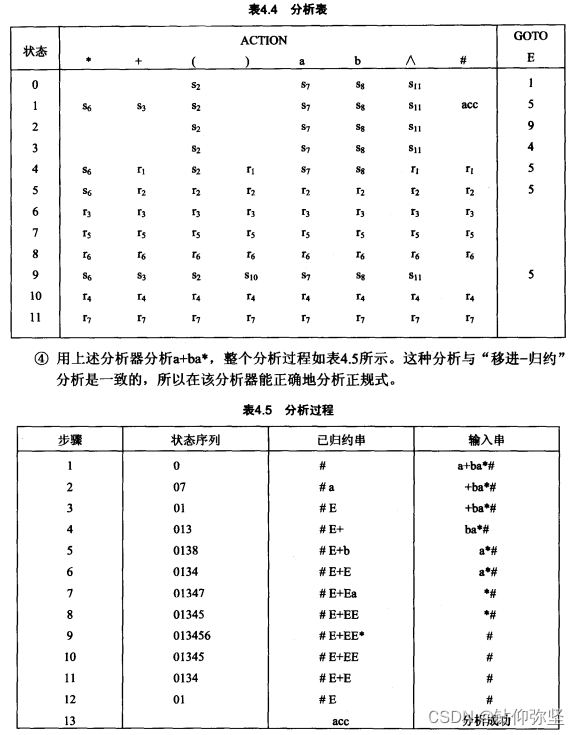
(2)按照(1)的说明所规定的解决二义性的准则，构造这个文法的LALR分析器。用这个分析器给出a+ba*的分析过程，并以此论证这个分析器能够正确的分析正规式。