目录标题

• 题目列表
• 第一题解析
• • 方法1：递归
  • 方法2：迭代
• 第二题解析
• • 解法一：递归
  • 解法二：迭代
• 第三题解析
• • 解法一：递归
  • 方法二：迭代
• 第四题解析
• • 方法一：递归
  • 方法二：迭代

题目列表

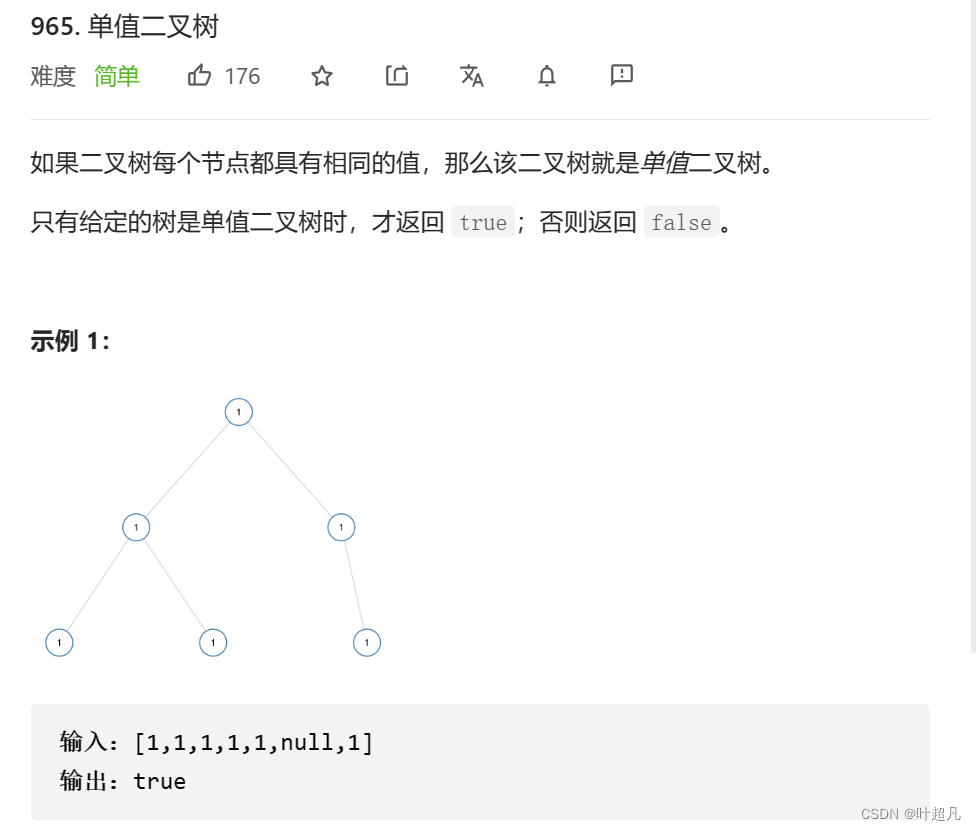
第一题：

点击此处来尝试此题
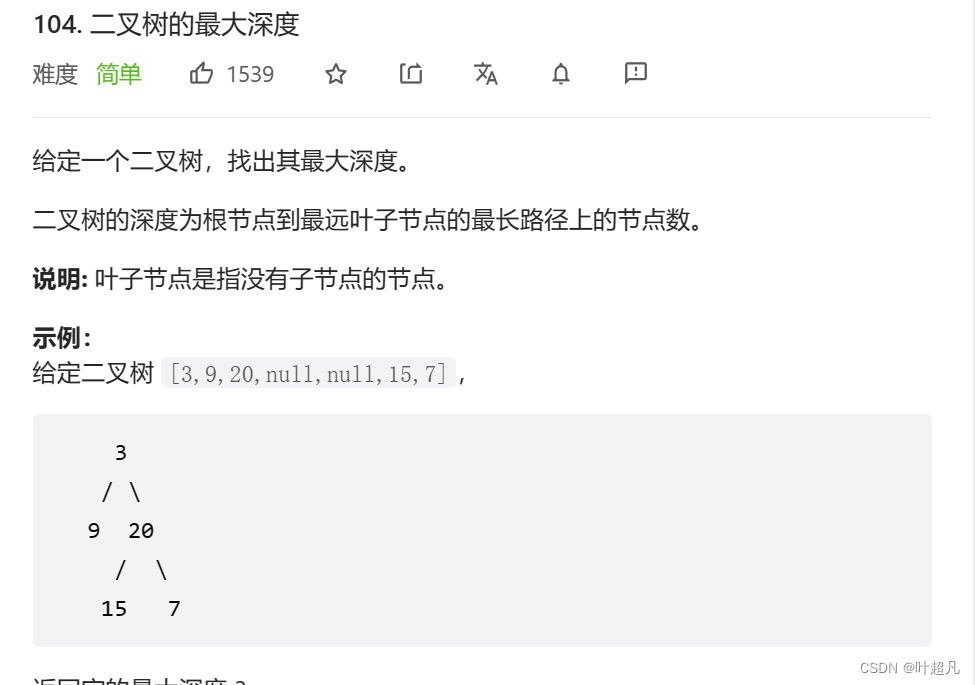
第二题：

点击此处来尝试此题
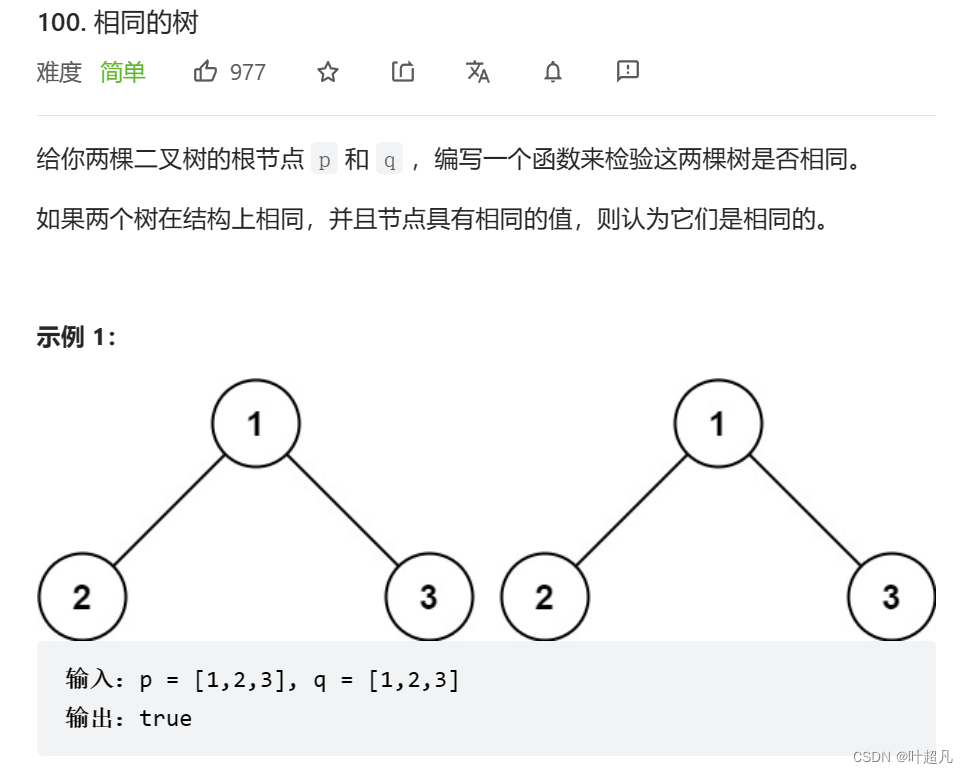
第三题：

点击此处来尝试此题
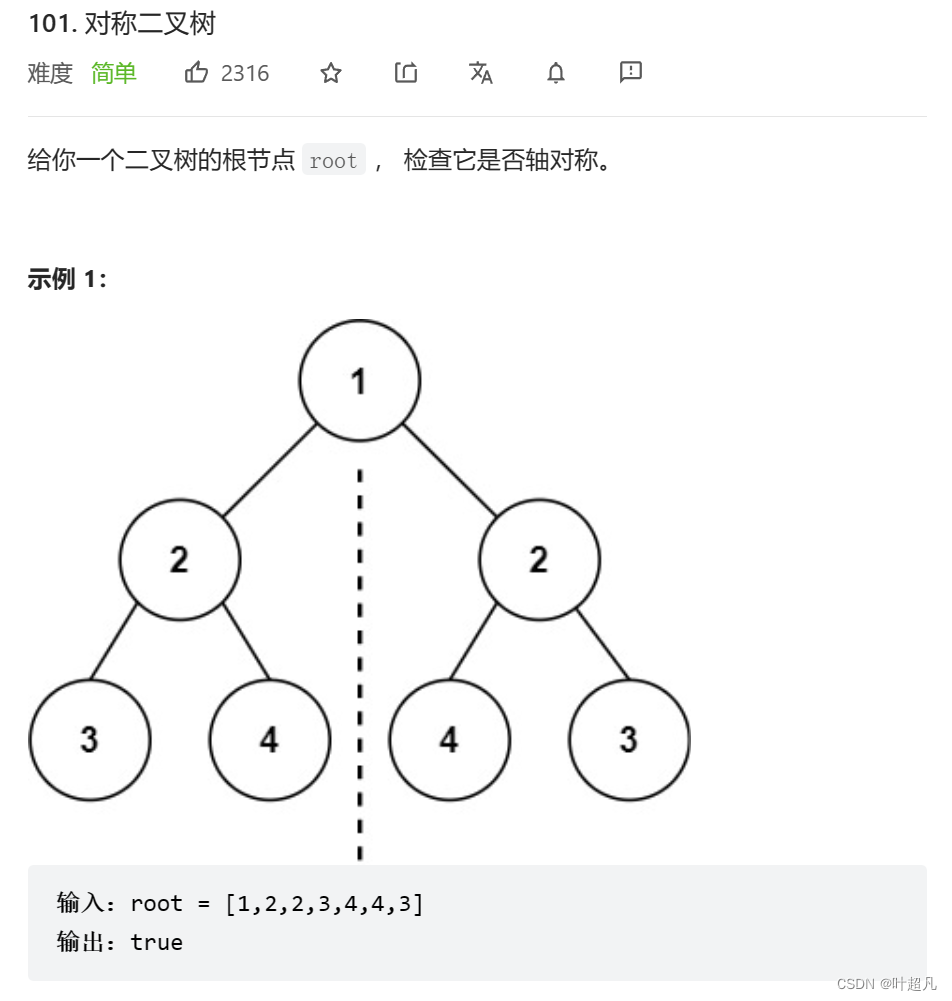
第四题：

点击此处来尝试此题

第一题解析

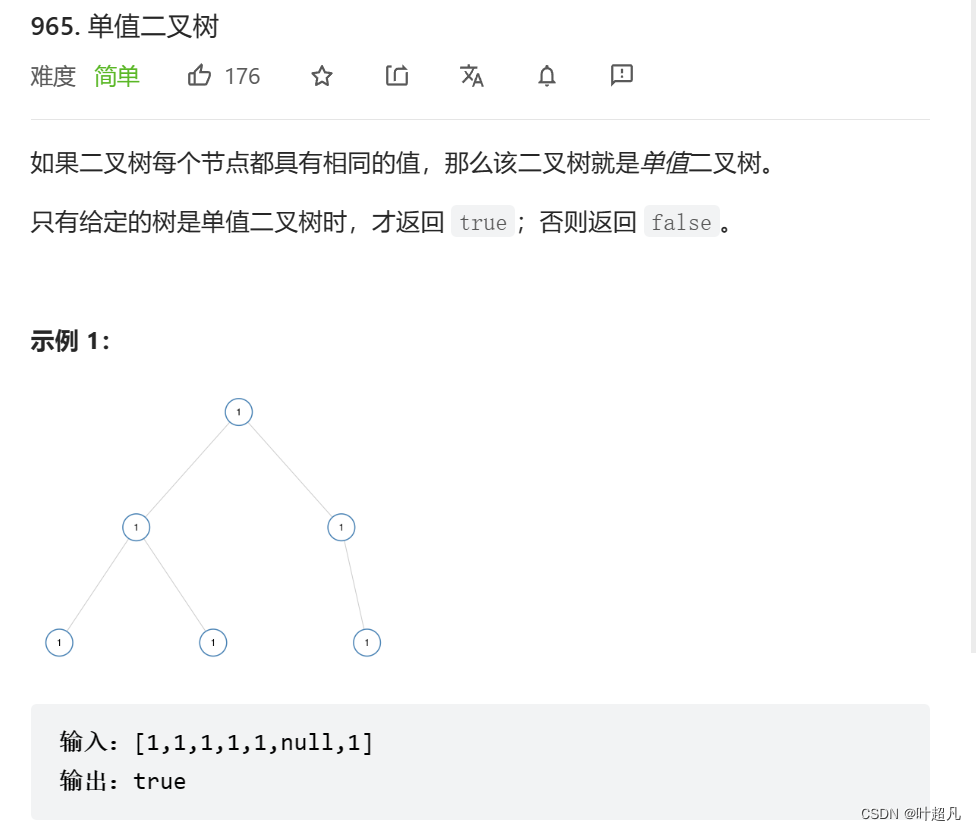
方法1：递归

判断一颗树是否为单值二叉树，我们可以采用深度优先的方式遍历树中的每个节点，因为深度优先得用到递归的方法来遍历二叉树，所以这里就得再创建一个函数来实现主要的功能，并且这个这个函数的返回值是一个整数，我们根据这个函数的返回值来判断是否是单值二叉树，如果函数的返回值是0的话就说明这个二叉树不是单值二叉树，如果这个函数的值为其他的话就说明这个二叉树是单值二叉树，一颗二叉树如果为单值二叉树的话，那么就说明这个树的左子树的节点都相等，右子树的所有节点也都相等，并且这两个子树的节点也都和根节点相等，所以在创建这个函数的时候我们声明两个参数一个参数用来表示是当前递归的方向，一个表示当前递归的节点是否和根节点的值相等

class Solution {
public:int is_univaltree(TreeNode* root,int val){}bool isUnivalTree(TreeNode* root) {return !is_univaltree(root,root->val);}
};

因为递归会遍历到每个节点，所以在函数体里面我们要判断每个节点里面的内容，首先如果一个节点为空的话那么这就说明当前空节点的左子树和右子树都是相当的并且不用继续递归往下判断，所以此时我们就直接返回0来结束此分支的判断，当此时节点的值不等于空的话我们就继续判断当前节点的值是否等于空节点，如果不等于的话我们就返回一个1来结束当前分支的判断，如果等于的话我们就继续往下判断，当程序来到这个位置的时候说明此时的节点既不为空也和根节点的值相等，那要想证明此时节点加上他的两颗子树是单值二叉树的话，我们是不是就得判断这个节点的左子树和右子树分别是不是单值二叉树，而这里的判断又可以用到这里的本函数，如果这个节点的左子树和右子树都是单值二叉树的话这两个函数的返回值向加就是0，只要有一个不是单值二叉树那么返回的结果就不是0，所以我们这里就可以把两个函数相加的返回值作为这个函数的返回值而这一步就是往下递归的过程，大家可以根据下面的图理解一下那么这里的代码就如下：

class Solution {
public:int is_univaltree(TreeNode* root,int val){if(root==nullptr){return 0;}if(root->val!=val){return 1;}return is_univaltree(root->left,val)+is_univaltree(root->right,val);}bool isUnivalTree(TreeNode* root) {return !is_univaltree(root,root->val);}
};

方法2：迭代

上面的方法是深度优先，他是先不停的判断左子树的节点是否和根节点相等再来不停的判断左子树的节点是否和根节点相等，也就是说先一直往左走走到头了再一直往右走，那么这是深度优先，而第二种方法的广度优先就完全不一样，他是一层一层的走先走第一层，当我们把第一层的节点遍历完之后再来遍历第二层的节点，而广度优先的实现方法和深度优先是不一样的，深度优先是通过递归的方法来实现而广度优先是通过迭代的方法来实现，既然是深度转广度的话我们这里就得创建一个队列来存储数据，并且二叉树含有多个数据所以得创建一个循环来不停的处理数据，当栈的数据为空时就表明二叉树的数据已经处理完了，所以为了防止一开始就无法进入循环，我们就得先将二叉树的根节点入队列当然这里还得先进行一下判断，当二叉树的根节点就为空时我们就直接返回true表明当前的二叉树为单值二叉树，那么这里的代码如下：

class Solution {
public:bool isUnivalTree(TreeNode* root) {if(root==nullptr){return true;}queue q;q.push(root);int val=root->val;while(!q.empty()){}}
};

因为这里要判断节点是否相等，所以每次循环我们都只处理一个节点，处理的方法就是将当前栈的顶部元素出栈并判断是否与二叉树的根节点的数据相等，如果不相等的话就直接返回false来结束当前函数，如果相等的话就将该节点的左节点和右节点入栈，并且入栈的时候得判断一下子节点是否为空如果为空的话就不入栈，当我们处理完一层节点时就已经将下一层的节点全部入栈了，接下来循环要处理的就是下一层的节点，并将下下层的节点不停的入栈，当循环结束的时候就说明当前二叉树的全部节点已经处理完了并且全部相等和根节点相等，所以这时我们就可以返回一个true表明当前的二叉树为单值二叉树。那么完整的代码如下：

class Solution {
public:bool isUnivalTree(TreeNode* root) {if(root==nullptr){return true;}queue q;q.push(root);int val=root->val;while(!q.empty()){TreeNode*tmp=q.front();q.pop();if(tmp->val!=val){return false;}if(tmp->right!=nullptr){q.push(tmp->right);}if(tmp->left!=nullptr){q.push(tmp->left);}}return true;}
};

第二题解析

解法一：递归

我们说采用递归方法解决问题的核心思路是将一个复杂的问题简单化，这里要计算一颗二叉树的最大深度那么就可以将其简化为求这个二叉树的两个子树的最大深度的最大值并加1，而求子树的最大深度又可以将其简化为求子树的两个子树的最大深度的最大值并加1，所以我们就可以一直这么递归下去直到遇到了空节点我们就返回0，表明当前左或者右子树的最大深度为0，如果没有遇到空节点那么就得继续递归下去，而递归的方法就是在函数返回的时候调用两次本函数一次计算左子树的最大深度一次计算右子树的最大深度并求其最大值加一，那么下面就是这个问题的代码：

class Solution {
public:int max_tree(TreeNode*root){if(root==nullptr){return 0;}return max(max_tree(root->right),max_tree(root->left))+1;}int maxDepth(TreeNode* root) {return max_tree(root);}
};

解法二：迭代

我们在使用迭代的方法求一棵树是否为单值二叉树的时候每次循环都只除理了一个节点并将这个节点的子节点入栈，那么对于这个问题我们就得做出更改，因为这里是判断二叉树的最大深度，所以每次循环我们都得处理当前层的所有节点并且将这些节点的子节点全部入到队列里面，同样的道理这里得对子节点做一些判断如果为空的话就不要入队列了，而且这里我们得创建一个变量num来记录当前队列的元素个数，通过num加while循环来处理当前层的节点，这个while循环是内部循环，在外层我们还得创建一个while循环来记录层的个数并且更新num的值，所以这里我们再创建一个变量depth来记录处理的层数，因为，每次内部循环我们都会将下一层的元素全部入队列，所以外层循环的结束条件就是当队列为空时我们就结束循环并且返回depth的值，那么这就是迭代方法实现的思路希望大家可以理解。

class Solution {
public:int maxDepth(TreeNode* root) {if(root==nullptr){return 0;}queue q;q.push(root);int depth=0;while(!q.empty()){int sz=q.size();while(sz){TreeNode*tmp=q.front();q.pop();if(tmp->right){q.push(tmp->right);}if(tmp->left){q.push(tmp->left);}--sz;}++depth;}return depth;}
};

第三题解析

解法一：递归

题目的要求是判断两棵二叉树是否相等？那么使用递归的方法就可以将此问题简化为判断两颗二叉树的根节点是否相等以及这两个根节点的左子树和右子树是否相等，题目提供的函数含有两个参数分别指向两颗二叉树的根节点并且这个函数的返回类型是bool类型，所以在写这道题目的时候就不用再创建函数了直接使用题目提供的函数就可以，在递归判断两颗二叉树是否相等的时，如果两颗二叉树的两个节点都为空的话表明此时的分支是相等的可以直接返回true，如果一个节点为空另外一个节点不为空的话就表明此时的两个分支不相等所以可以直接false来结束此递归，如果在递归的时候两个节点的值不相等的话就表明此时的分支是不相等的直接返回false，那么上述的情况其代码就如下：

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if((p==q)&&(p==nullptr)){return true;//表明两个节点都为空}else if((p==nullptr)||(q==nullptr)){return false;//表明两个节点只有一个为空}else if(p->val!=q->val){return false;//表明两个节点都不为空//但是两个节点的值不相等}else{//表明此时两个节点都不为空且值相等}}
};

当执行的顺序来到了最后的else语句时表明此时的两个节点都不为空且值还相等，所以此时要判断两棵树是否相等，就取决于这两个节点的左子树和右子树是否相等，所以就可以把上述的判断结果作为此函数的返回值来结束这个函数，而判断两个数是否相等又得用到isSameTree函数，所以在返回的时候又会调用本函数来进行递归判断，那么这就是递归的过程大家可以自行画图来理解理解，那么这里的代码就如下：

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if((p==q)&&(p==nullptr)){return true;//表明两个节点都为空}else if((p==nullptr)||(q==nullptr)){return false;//表明两个节点只有一个为空}else if(p->val!=q->val){return false;//表明两个节点都不为空//但是两个节点的值不相等}else{return isSameTree(p->right,q->right)&&isSameTree(p->left,q->left);            //表明此时两个节点都不为空且值相等//那么这时就要判断这两个节点的左右子树是否相等}}
};

我们将其测试一下发现是可以运行的：

方法二：迭代

我们使用迭代的方法判断一棵树是否为单值二叉树和求一棵树的最大深度时都是创建的一个队列，那么使用迭代的方法来判断两颗二叉树是否相等的时候就得创建两个队列，同样的思路首先得判断函数的两个参数是否都为空，如果都为空的话就直接返回true表明此时的二叉树是相等的，如果有一个为空一个不为空的话就表明这两个二叉树是不相等的就返回false,当两个节点都不为空的话就可以创建两个队列并将两个节点分别插入到队列里面去，再创建一个while循环其循环继续的条件就是当两个队列都不为空，那么这里的代码就如下：

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p==nullptr&&q==nullptr){return true;}if(p==nullptr||q==nullptr){return false;}queue q1,q2;q1.push(p);q2.push(q);while(!q1.empty()&&!q2.empty()){}}
};

在循环里面要对两个队列分别进行处理，处理的方式就是将两个队列的头元素出队列然后对这两个元素的数据进行判断如果数据不相同的话就返回false如果相同的话就对这两个元素的左右节点进行判断：如果两个元素的右节点有一个为空另外一个不为空的话，那么这两个二叉树肯定是不相等的就直接返回flase，对于左节点也是同样的道理，那么这里的代码就如下：

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p==nullptr&&q==nullptr){return true;}if(p==nullptr||q==nullptr){return false;}queue q1,q2;q1.push(p);q2.push(q);while(!q1.empty()&&!q2.empty()){TreeNode*node1=q1.front();q1.pop();TreeNode*node2=q2.front();q2.pop();if(node1->val!=node2->val){return false;}if(node1->right==NULL^node2->right==NULL){return false;}if(node1->left==NULL^node2->left==NULL){return false;}}}
};

当程序走完上面的判断时只剩下这几种可能要么两个节点的左节点都为空要么都不为空，右节点也是同样的道理，所以接下来要做的判断就是如果子节点不为空的话我们就将该节点入队列，那么这就是循环里面要做的事，当循环结束的时候此时的两个队列有两种可能要么两个队列都为空要么就只有一个队列为空，当队列都为空时说明此时的二叉树是相同的，如果只有一个为空说明此时的二叉树不相同，那么这里完整的代码就如下：

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p==nullptr&&q==nullptr){return true;}if(p==nullptr||q==nullptr){return false;}queue q1,q2;q1.push(p);q2.push(q);while(!q1.empty()&&!q2.empty()){TreeNode*node1=q1.front();q1.pop();TreeNode*node2=q2.front();q2.pop();if(node1->val!=node2->val){return false;}if((node1->right==NULL)^(node2->right==NULL)){return false;}if((node1->left==NULL)^(node2->left==NULL)){return false;}if(node1->right!=NULL){q1.push(node1->right);}if(node1->left!=NULL){q1.push(node1->left);}if(node2->right!=NULL){q2.push(node2->right);}if(node2->left!=NULL){q2.push(node2->left);}}return q1.empty()&&q2.empty();}
};

测试一下是可以编译成功的：

第四题解析

方法一：递归

首先我们来看看什么是对称二叉树，我们在二叉树的根节点处做一根竖直的横线，如果二叉树的左边和右边关于这根横线对称的话就是对称二叉树，我们来看看下面这样图：

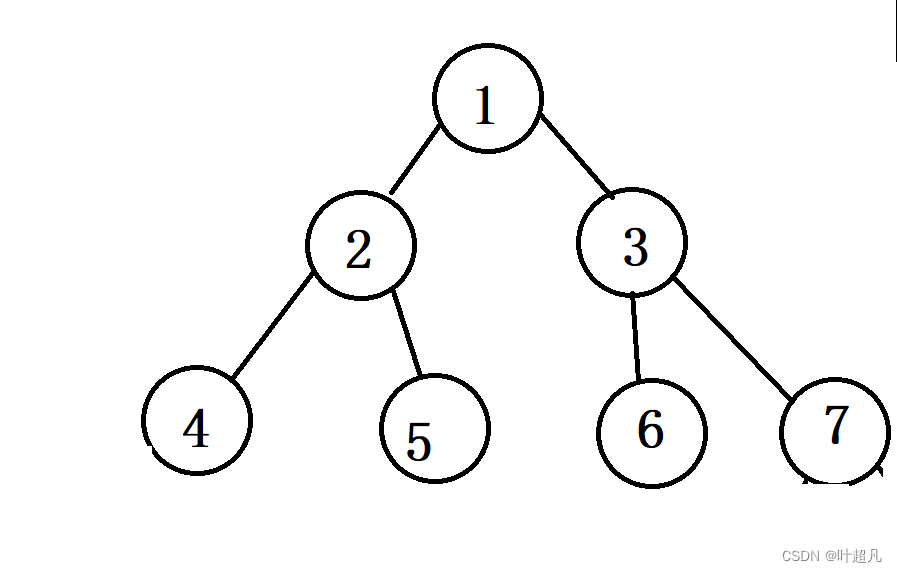
这是我们的二叉树，如果我们要判断他是否为对称二叉树的话就得判断他是否关于下面这条直线对称：

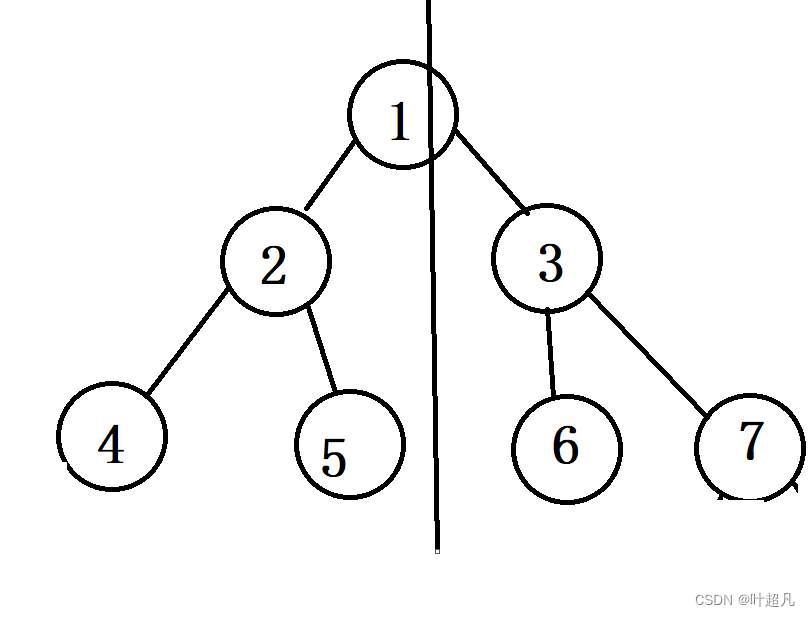
但是通过这样方法给大家讲讲解问题的话理解成本太大了，所以我们把这条线放到二叉树的旁边去，并且再将这个二叉树拷贝一份放到这条线的另一边：

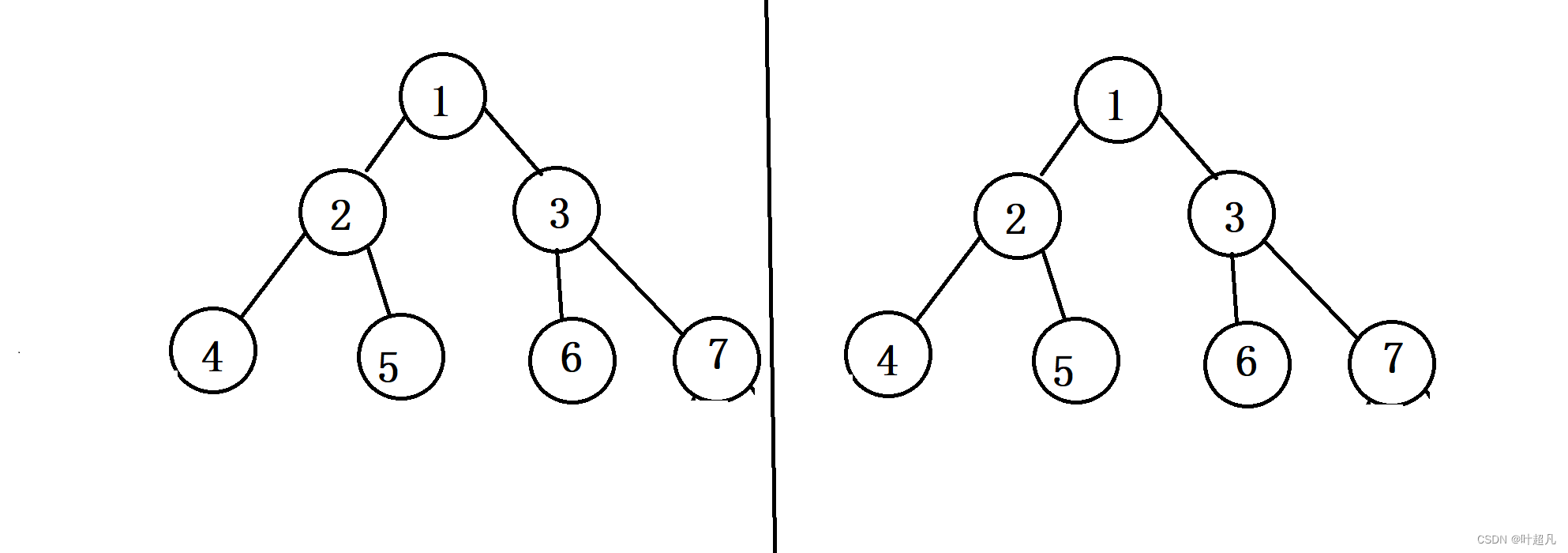
这样的话我们就将题目修改成了判断两个二叉树是否关于一条直线对称，既然这里有两个二叉树的话我们就得再创建一个函数并且这个函数有两个TreeNode*参数，那么这里的代码就如下：

class Solution {
public:bool is_Symmetric(TreeNode* root1,TreeNode*root2){}bool isSymmetric(TreeNode* root) {}
};

首先这里我们要知道的一点就是is_Symmetric函数的功能是判断两棵树是否关于对称轴对称，然后我们再来实现这个函数的定义，首先判断两颗树是否对称的时候我们得先判断这两颗树的根节点是否相等，也就是判断这两颗树的1号节点是否相等，如果两棵树的1号节点都为空的话说明这个节点下面是没有分支的，说明此时的二叉树是对称的，如果两个节点有一个为空一个为非空的话，说明此时的二叉树不是对称的，我们就返回false，如果两个节点都为非空但是值不相等的话说明此时的二叉树也不是对称的，所以我们就直接返回false，那么这里的代码如下：

class Solution {
public:bool is_Symmetric(TreeNode* root1,TreeNode*root2){if(root1==nullptr&&root2==nullptr){return true;}if(root1==nullptr||root2==nullptr){return false;}if(root1->val!=root2->val){return false;}}bool isSymmetric(TreeNode* root) {return is_Symmetric(root,root);}
};

我们说递归的核心思想是将复杂的问题简单话，我们要判断两个二叉树是否关于一个直线对称，可以将其简化为判断两个树的根节点是否相等（把左边的树称为左树，右边的树称为右树）以及左树的根节点的左子树是否和右数的根节点的右子树对称，以及左数的根节点的右子树是否和右树的左子树是否相等，而函数is_Symmetric的功能就是判断两颗二叉树是否对称的，当两个二叉树的根节点已经相同时，此时二叉树是否对称就由这两个根节点的子树决定，所以这个函数的返回值就是调用两次函数来判断这两个函数的子树，所以完整的代码就如下：

class Solution {
public:bool is_Symmetric(TreeNode* root1,TreeNode*root2){if(root1==nullptr&&root2==nullptr){return true;}if(root1==nullptr||root2==nullptr){return false;}if(root1->val!=root2->val){return false;}return is_Symmetric(root1->right,root2->left)&&is_Symmetric(root1->left,root2->right);}bool isSymmetric(TreeNode* root) {return is_Symmetric(root,root);}
};

方法二：迭代

如果一棵树是对称的话那么这棵树的每一层的节点都是对称的，所以这里就可以创建一个队列和循环来处理数据，我们来看看下面这张图：

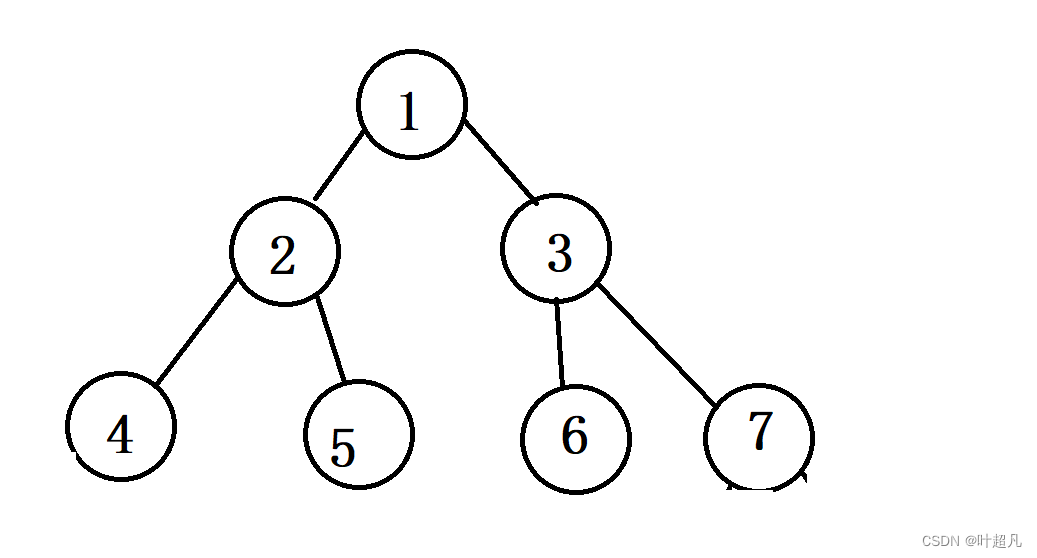
如果这棵树是对称二叉树的话，那么第二层的2 3号节点是相同的，第三层的4 7号节点是相同的，5 6号节点是相同的，上面在判断单值二叉树的时候因为比较的元素有一个一直不变所以每次循环都只处理一个数据，但是这里不一样每次比较的两个元素都在发生变化，所以每次循环都得处理两个数据，所以在循环的外面我们先判断根节点是否为空，如果为空的话就直接返回true，如果不为空的话我们就入两次根节点，当队列的元素为空时表明二叉树已经处理完了，所以while循环结束的条件就是当队列为空时结束循环，那么这里的代码就如下：

class Solution {
public:bool isSymmetric(TreeNode* root) {if(root==nullptr){return true;}queue q1;q1.push(root);q1.push(root);while(!q1.empty()){}}
};

因为这里要判断二叉树是否对称所以不管子节点是否为空我们都要将其入队列，所以在循环里面首先得将前两个元素出队列并进行判断，如果两个节点一个为空一个不为空或者两个节点的值不相等的话就表明此时的二叉树不对称，如果两个节点都为空的话就继续往下判断，那么这里的代码如下：

class Solution {
public:bool isSymmetric(TreeNode* root) {if(root==nullptr){return true;}queue q1;q1.push(root);q1.push(root);while(!q1.empty()){TreeNode*node1=q1.front();q1.pop();TreeNode*node2=q1.front();q1.pop();if(node1==nullptr&&node2==nullptr){continue;}if(node1==nullptr||node2==nullptr){return false;}if(node1->val!=node2->val){return false;}}}
};

当程序走完上述的判断就表明此时的这两个节点的值相等且不为空，一开始将两个头节点入队列所以这时就相当于创建了两棵树：

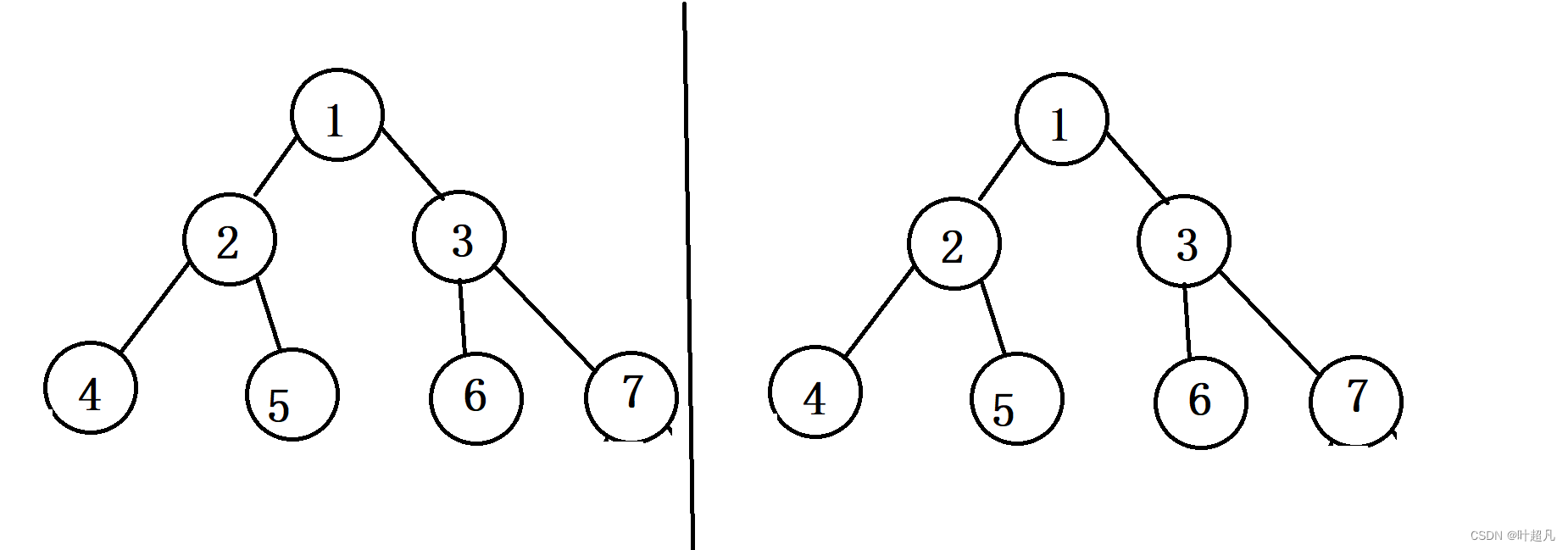
当判断完根节点对称之后就得判断其子节点是否对称，这里使用的容器是队列，队列的处理规则是先入先处理所以将子节点入队列的时候就得将对应位置上的元素连着入队列，比如说我们处理完了两个树的1号节点之后就得将左数的2号节点和右树的3号节点一起入队列，将左树的3号节点和右树的2号节点一起入队列，那么这里的代码就如下：

class Solution {
public:bool isSymmetric(TreeNode* root) {if(root==nullptr){return true;}queue q1;q1.push(root);q1.push(root);while(!q1.empty()){TreeNode*node1=q1.front();q1.pop();TreeNode*node2=q1.front();q1.pop();if(node1==nullptr&&node2==nullptr){continue;}if(node1==nullptr||node2==nullptr){return false;}if(node1->val!=node2->val){return false;}q1.push(node1->left);q1.push(node2->right);q1.push(node1->right);q1.push(node2->left);}return true;}
};

希望大家可以理解。