文章目录

• 1.随机变量（Random Variable）
• 2.概率密度函数（Probability Density Function, PDF）
• 3.期望（Expectation）
• 4.随机抽样（Random Sampling）

1.随机变量（Random Variable）

随机变量（Random Variable） 是一个未知的量，它的值取决于一个 随机事件（Random events） 。以抛硬币为例，抛硬币就是一个 随机事件 。正面朝上记为0，反面朝上记为1，因此抛硬币的结果就是一个 随机变量XXX 。

注意： 通常用大写字母XXX表示随机变量；用小写字母xxx表示随机变量的观测值。例如抛硬币：

• 第1次是正面，则x1=0x_{1}=0x1​=0；
• 第2次是反面，则x2=1x_{2}=1x2​=1；
• 第3次是正面，则x3=0x_{3}=0x3​=0；
• 第4次是正面，则x4=0x_{4}=0x4​=0；

2.概率密度函数（Probability Density Function, PDF）

概率密度函数（PDF）表示了：随机变量 XXX 在某个确定的点 x=x0x=x_0x=x0​ 附近取值的可能性。

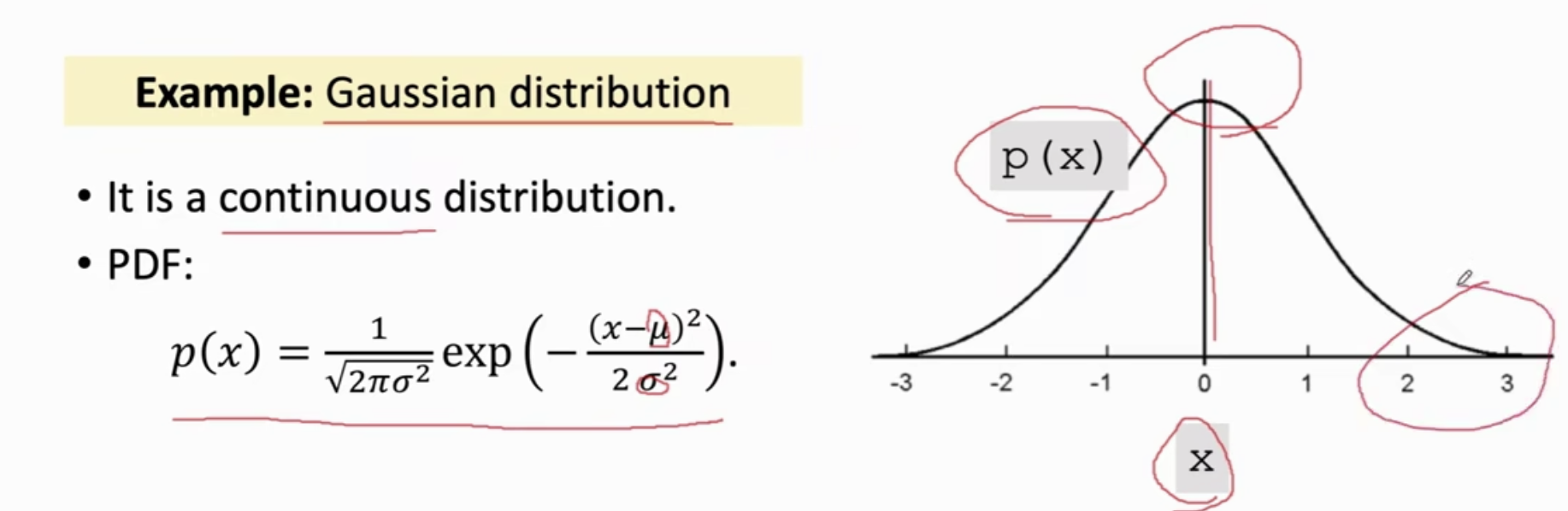
理解1： 以高斯分布/正态分布（Gaussian distribution）为例。高斯分布是个连续的概率分布，它的概率密度函数PDF公式为：
p(x)=12πσ2exp⁡(−(x−μ)22σ2)p(x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)p(x)=2πσ2​1​exp(−2σ2(x−μ)2​)

其中，随机变量 XXX 的取值可以是任意实数 x∈Rx\in \mathcal{R}x∈R，μ\muμ是均值，σ\sigmaσ是标准差 。

高斯分布的图像如下图所示。在高斯分布的概率密度函数PDF图像中，横轴 xxx 是随机变量 XXX 的取值，纵轴 p(x)p(x)p(x) 是随机变量的概率密度，曲线 p(x)p(x)p(x) 是高斯分布的概率密度函数 p(x)p(x)p(x)。图像说明了：xxx 在原点（ x=0x=0x=0 ）附近取值的概率比较大；在远离原点的地方（ x=∞x=\inftyx=∞ ）取值的概率比较小。

理解2： 以离散的概率分布为例，如下图所示。 随机变量 XXX 的取值只能是离散的值 X∈{1,3,7}X \in \{1, 3, 7\}X∈{1,3,7}。

离散的概率分布的概率密度函数PDF表示了随机变量 XXX 在 1、3、7 这三个点取值的可能性（概率）：

• p(1)=0.2p(1) = 0.2p(1)=0.2 说明：随机变量 XXX 在 x=1x=1x=1 时取值的概率概率为0.2 （x=1的概率为0.2）；
• p(3)=0.5p(3) = 0.5p(3)=0.5 说明：随机变量 XXX 在 x=3x=3x=3 时取值的概率概率为0.5 （x=3的概率为0.2）；
• p(7)=0.3p(7) = 0.3p(7)=0.3 说明：随机变量 XXX 在 x=7x=7x=7 时取值的概率概率为0.3 （x=7的概率为0.3）；
• 同时还说明在其他地方的取值为0。

概率密度函数PDF的性质（令随机变量 XXX 的定义域为 X\mathcal{X}X ）：

• 对于连续型随机变量 XXX 的概率密度函数PDF，随机变量 XXX 积分的值等于1，即：
  ∫x∈Xp(x)dx=1\int_{x\in\mathcal{X}}^{} p(x) dx = 1∫x∈X​p(x)dx=1
• 对于离散型随机变量 XXX的概率密度函数PDF，随机变量的和的值等于1，即：
  ∑x∈Xp(x)=1{\textstyle \sum_{x\in\mathcal{X}}^{} p(x)=1} ∑x∈X​p(x)=1

3.期望（Expectation）

期望的定义（令随机变量 XXX 的定义域为 X\mathcal{X}X ）：

• 连续型随机变量 XXX 的期望：
  E[f(x)]=∫x∈Xp(x)⋅f(x)dx\mathbb{E}[f(x)]=\int_{x\in\mathcal{X}}^{} p(x)\cdot f(x)dxE[f(x)]=∫x∈X​p(x)⋅f(x)dx

• 离散型随机变量 XXX 的期望：
  E[f(x)]=∑x∈Xp(x)⋅f(x)\mathbb{E}[f(x)]=\textstyle \sum_{x\in\mathcal{X}}^{} p(x)\cdot f(x)E[f(x)]=∑x∈X​p(x)⋅f(x)

理解：

p(x)p(x)p(x) 是随机变量 XXX 观测值 xxx 的概率，f(x)f(x)f(x) 是随机变量 XXX 观测值 xxx 出现的次数。以掷色子为例：

p(x=1)=16p(x=1)=\frac 1 6p(x=1)=61​，f(x)=10f(x)=10f(x)=10 的含义：其中 p(x=1)p(x=1)p(x=1) 表示色子点数为1出现的概率为16\frac 1 661​，f(x)=10f(x)=10f(x)=10 表示色子点数为1出现的次数为10次。

4.随机抽样（Random Sampling）

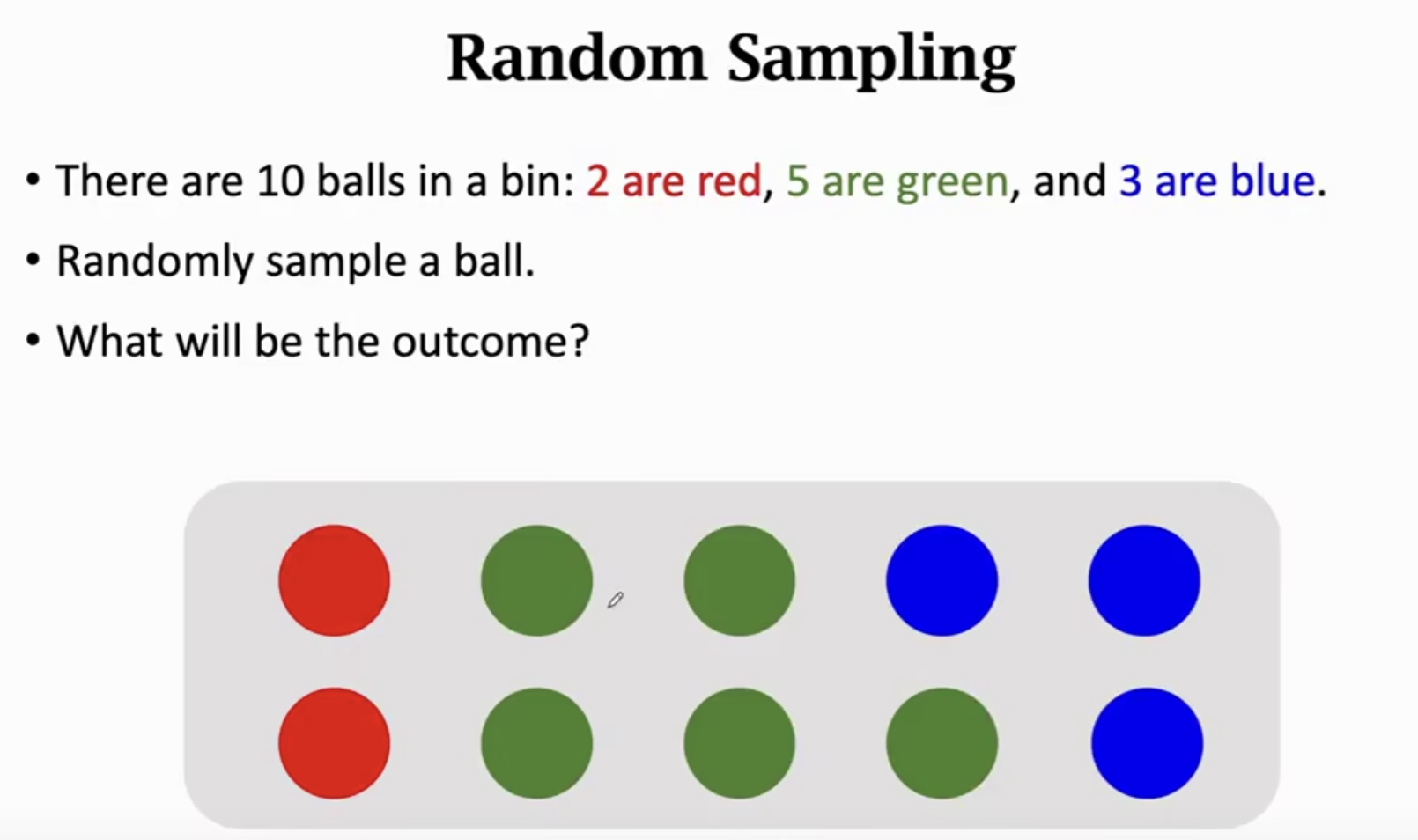
随机抽样： 按照随机原则，利用随机数，从总体中抽取样本的方法。