作者：一个喜欢猫咪的的程序员 

专栏：《数据结构》

喜欢的话：世间因为少年的挺身而出，而更加瑰丽。                                  ——《人民日报》

---

目录

1.二叉树的概念及结构

1.1二叉树的概念

1.2二叉树的类型分类：

 1.3二叉树的结构

2.接口实现及其具体细节的讲解 

2.1知识铺垫：二叉树的遍历方式

2.2前中后序遍历代码实现：

2.2.1前序遍历（PreOrder）：

2.2.2中序遍历（InOrder）：

2.2.3后序遍历（PostOrder）:

2.3二叉树的节点个数和叶节点个数：

2.3.1二叉树节点的个数（TreeSize）：

2.3.2二叉树叶子节点的个数（TreeLeafSize）

2.4树的高度及二叉树第K层的节点个数

2.4.1树的高度（TreeHeight）：

2.4.2二叉树第K层的节点个数（TreeLevelSize）：

2.5二叉树查找值为x的节点（TreeFind）：

2.6层序遍历（LevelOrder）：

2.7判断二叉树是否是完全二叉树及二叉树销毁

2.7.1判断二叉树是否是完全二叉树（BinaryTreeComplete）

2.7.2二叉树销毁（TreeDestory）：

3.完整代码：

3.1test.c文件(二叉树实现):

3.2Queue.h文件：

3.3Queue.c文件：

---

1.二叉树的概念及结构

1.1二叉树的概念

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。

1.2二叉树的类型分类：

二叉树分为两种：

• 完全二叉树
• 满二叉树

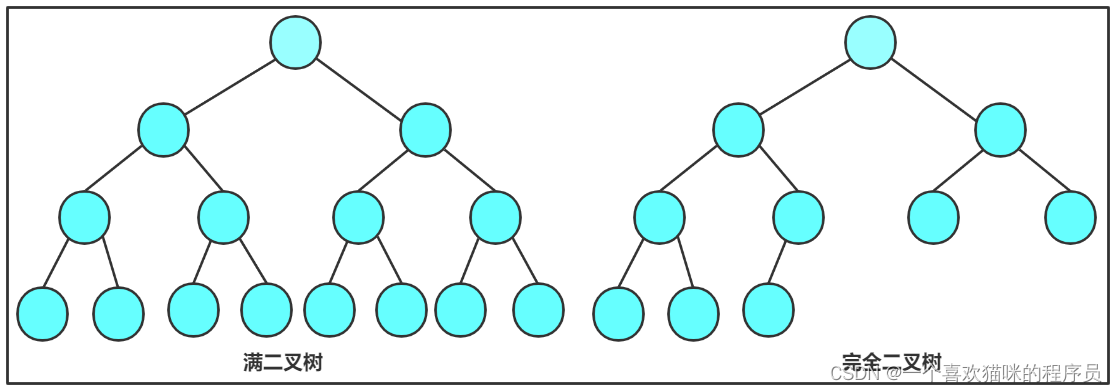
 1.3二叉树的结构

由上图可知，二叉树是一个节点root，链接着一个左节点left和一个右节点right。

定义二叉树的结构：

typedef int BTDataType;
typedef struct BinaryTreeNode
{//二叉树的结构BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

创建二叉树节点：

BTNode* BuyBTNode(BTDataType x)
{BTNode*newnode=(BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}

 在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树.

这里手动链接各方便大家理解后面的操作，以及对测试用例的修改来测试接口函数是否正确符合要求.

//构造二叉树BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);BTNode* n7 = BuyBTNode(7);n1->left = n2;//链接二叉树n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;n3->left = n7;

2.接口实现及其具体细节的讲解 

2.1知识铺垫：二叉树的遍历方式

遍历顺序分为4种：（root为根节点）

• 前序遍历：root  左子树 右子树
• 中序遍历：左子树 root  右子树
• 后序遍历：左子树 右子树  root
• 层序遍历：一层一层遍历（后面会单独讲）

 如：前序遍历是每颗子树都先遍历root节点，再遍历左子树，最后在遍历右子树。

以下图为例：我们来了解一下前序遍历的顺序。

先root节点出1，然后是1的左子树（以2为根节点的子树）出2，再到2的左子树出3，再出3的左子树NULL，然后返回3的位置再走3的右子树然后出NULL，再返回2走2的右子树出NULL再返回到1的位置，1的右子树也是如此，以此类推。

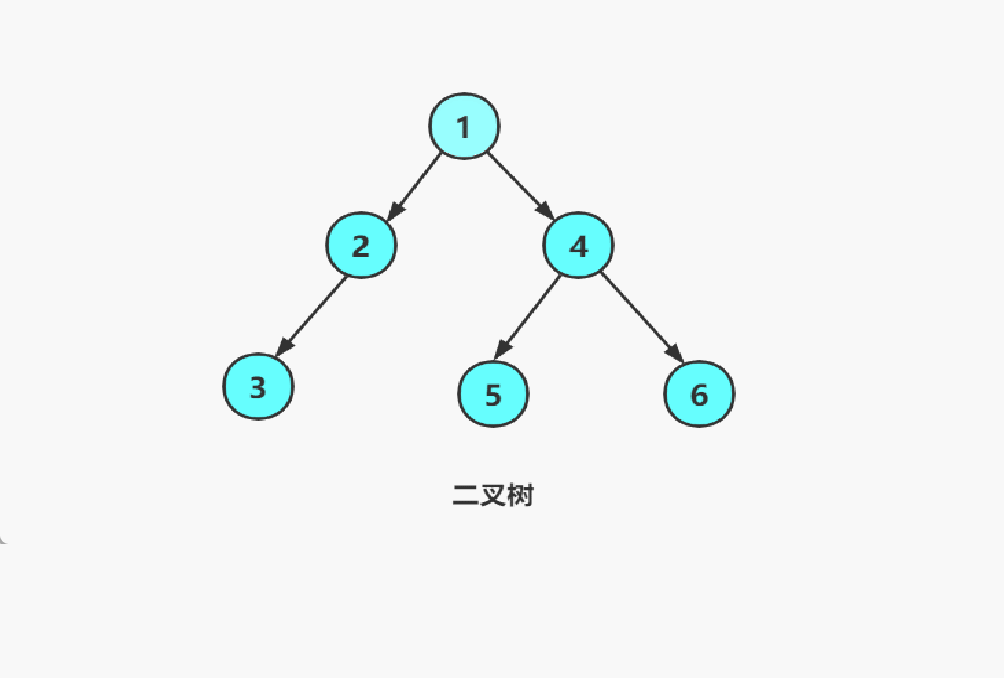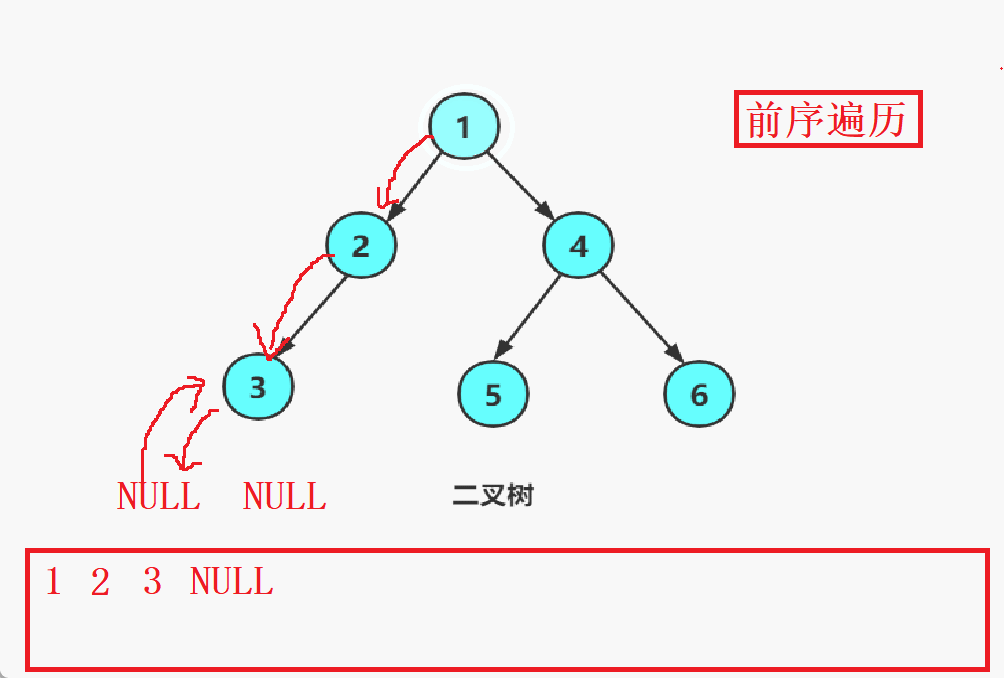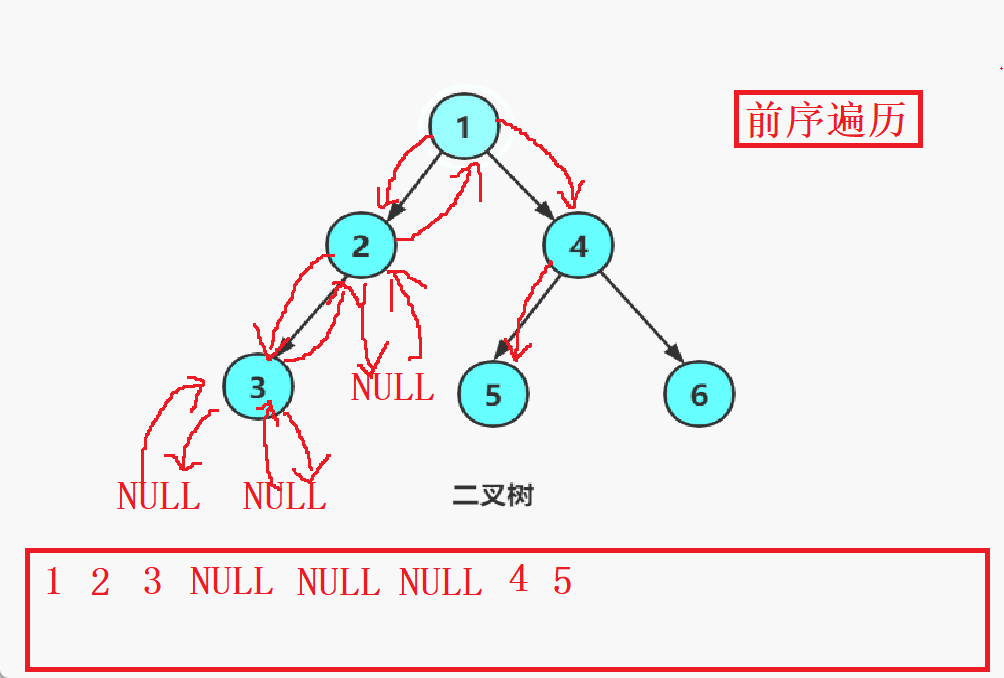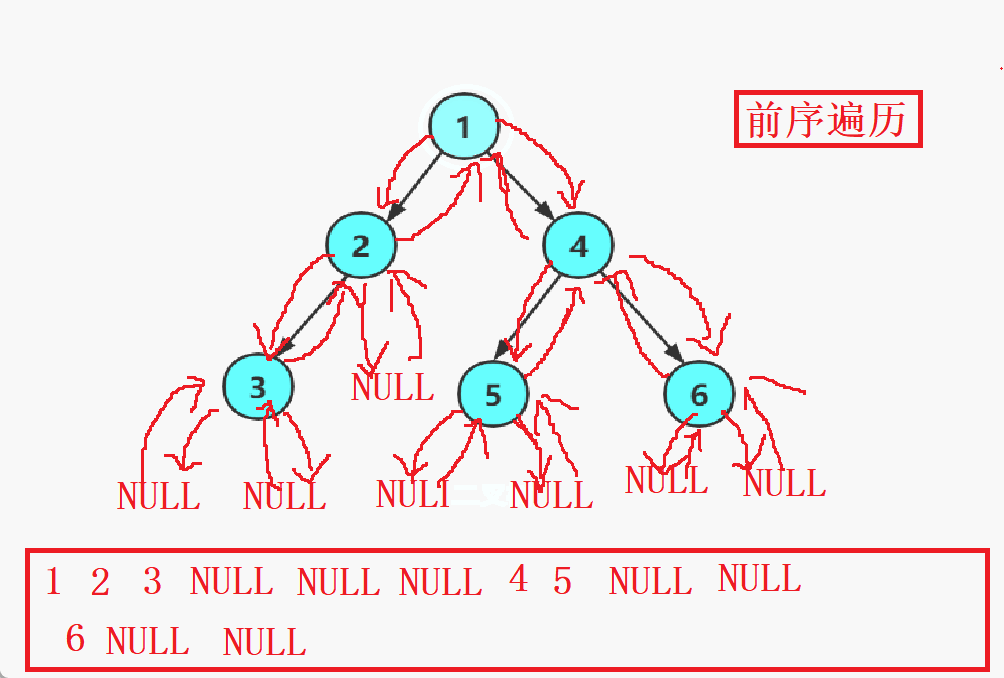
还是以上图为例子，前中后序的顺序如下：

2.2前中后序遍历代码实现：

2.2.1前序遍历（PreOrder）：

前序遍历的遍历顺序：root  左子树 右子树

将一个二叉树分为根节点、左子树和右子树，它的子树也是可以这样分。

这样的操作是重复的，因此可以看成一个递归的底层过程。

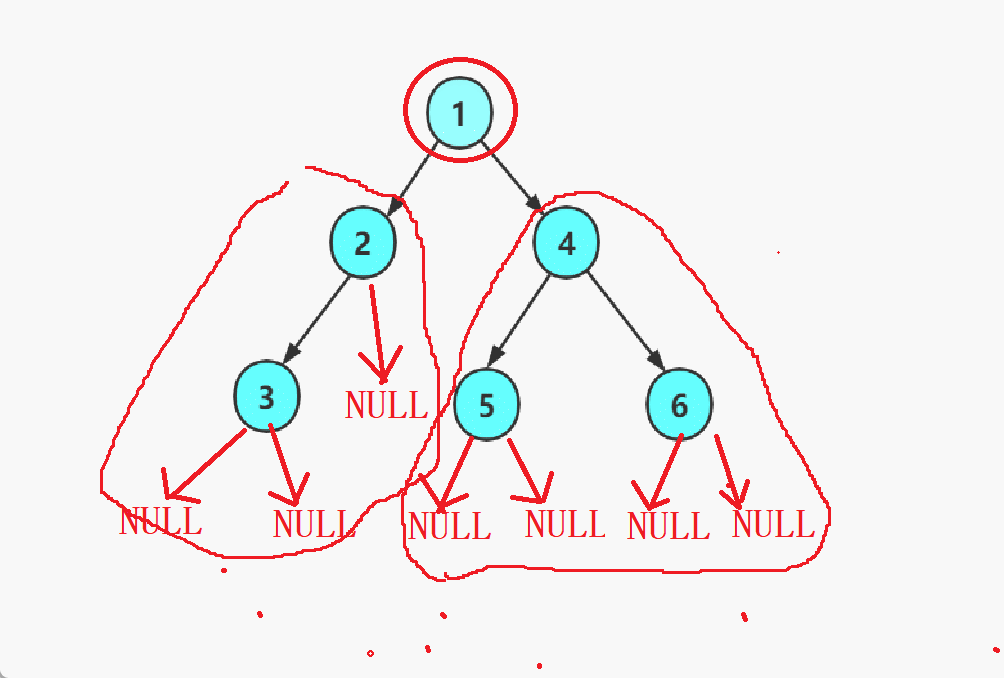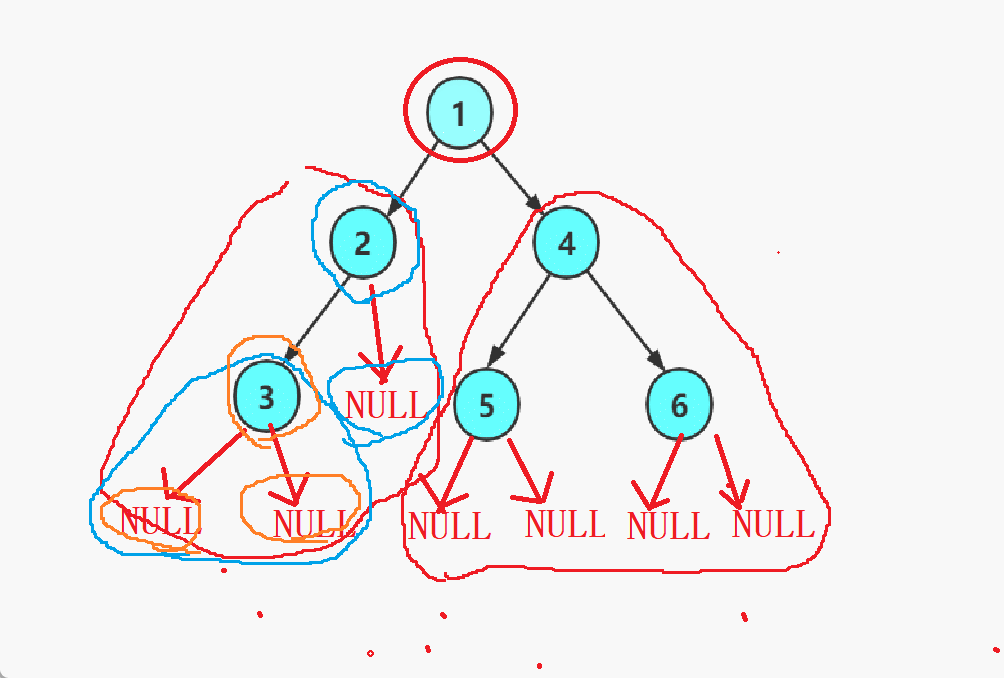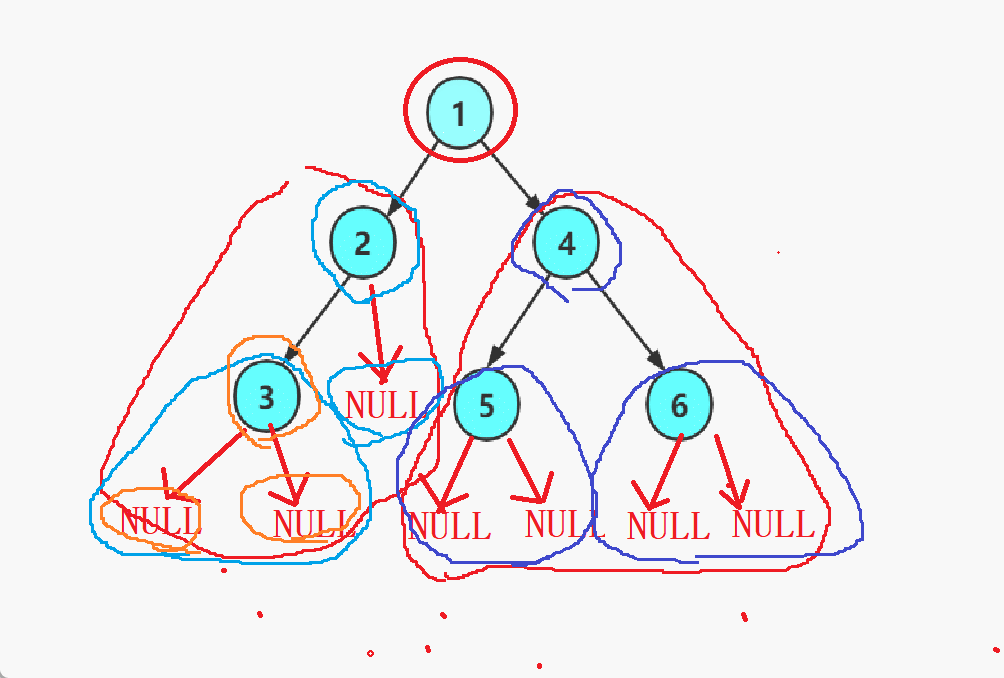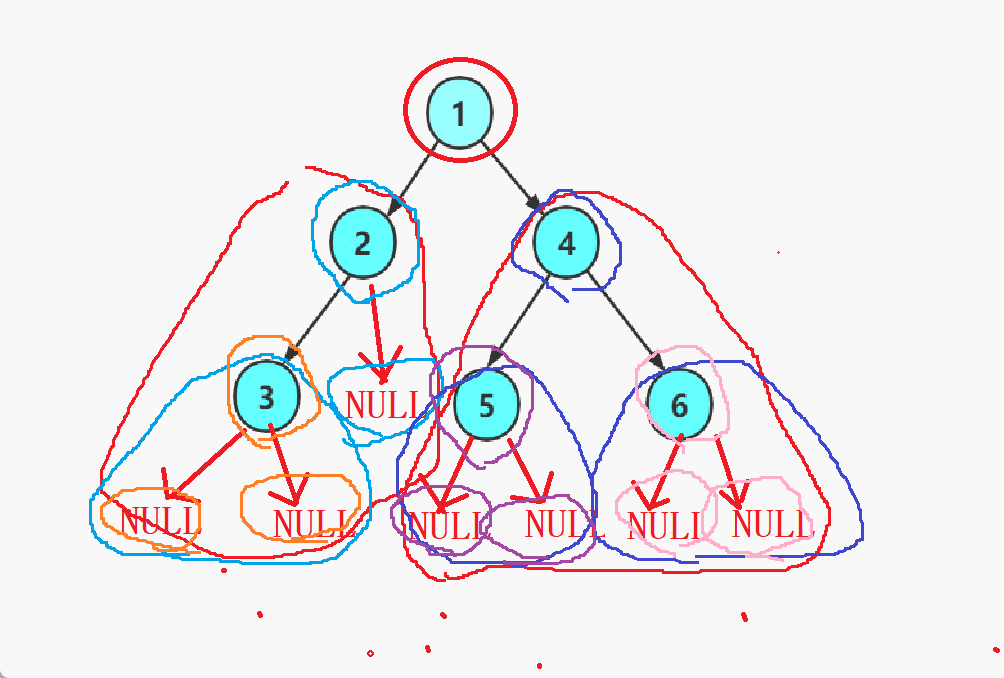
 只看最下面的部分的话

• 当root为NULL时，打印NULL。
• 当root不为NULL时，打印root->data的值。

只看最顶部 1 2 4的时候。

先打印root（1）,然后递归找到左子树（2）打印2，再递归找到右子树（4）打印4。

从局部映射到整体后，函数递归写法就是如此。

// 二叉树前序遍历
void PreOrder(BTNode* root)
{//assert(root);if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}

2.2.2中序遍历（InOrder）：

中序遍历与前序遍历不相同的地方就是在打印的先后顺序不同

因此递归的前后顺序随着改变。

// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

2.2.3后序遍历（PostOrder）:

// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

2.3二叉树的节点个数和叶节点个数：

2.3.1二叉树节点的个数（TreeSize）：

二叉树节点的个数，可以看成左子树的节点个数+右子树的节点个数+1（根节点）。

遇到NULL返回0。

当只有1个节点时，它也有左子树(NULL)和右子树（NULL）。 

当树为 1 2 4时，1的左子树为2，右子树为4。那2和4的左子树和右子树又是相当于只有一个节点的情况。

...

扩张到n个节点的情况下，就是递归不断向下找并且返回的过程。

// 二叉树节点个数
int TreeSize(BTNode* root)
{if (root == NULL)return 0;return TreeSize(root->left) + TreeSize(root->right) + 1;
}

2.3.2二叉树叶子节点的个数（TreeLeafSize）

计算叶子结点的个数，又跟就是二叉树节点个数不太一样

叶节点代表它没有左右节点了，也就是左右节点皆为NULL

• 当左右左右节点皆为NULL时返回1
• 叶节点数等于左子树的叶子个数+右子树的叶子个数

// 二叉树叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

2.4树的高度及二叉树第K层的节点个数

2.4.1树的高度（TreeHeight）：

设根节点的层数为1。

当只有一层的时候，左子树为0，右子树为0层，总层数为 1层。

当有2层时，左子树为1，右子树为1层，总层数为1+1层。

当有3层时，左子树为2，右子树为2层，总层数为2+1层。

....

当有N层时，左子树为N-1层，右子树为N1层，总层数为（N-1）+1层。

• 这样就可以将树的高度看成较高子树的层高+1（根节点的那一层）。因此将左右子树的层数计算出来，让他们较大的一个+1就是二叉树的高度了。

//树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left+1 : right+1;
}

2.4.2二叉树第K层的节点个数（TreeLevelSize）：

可以通过左右子树，让他们可下降k-1层，就到达了第k层

如果到了第k层就说明节点就是第k层的其中一个节点就返回1就好了。

如果为NULL，就返回0。

// 二叉树第k层节点个数
int TreeLevelSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1 )//当k==1时，刚好是第三层return 1;return TreeLevelSize(root->left, k - 1) + TreeLevelSize(root->right, k - 1);
}

2.5二叉树查找值为x的节点（TreeFind）：

依旧不断通过左子树和右子树分别遍历下去

找到等于x的值，就返回那个节点的地址

遇到NULL时，返回NULL

当全部找完依旧没找到，那就返回NULL。

// 二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x) 
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* left = TreeFind(root->left,x);if (left)return left;BTNode* right = TreeFind(root->right, x);if (right)return right;return NULL;
}

2.6层序遍历（LevelOrder）：

这里需要用到队列，不懂队列可以先看看另外一篇博客：http://t.csdn.cn/sLlHK

这里就直接使用队列了。

• 先让根节点进入队列
• 将队头用一个变量保存下来，如果不为NULL就将其打印
• 再将队头pop一下
• 当左右节点存在，就将其push进去队列，以此循环

//层序遍历
void LevelOrder(BTNode* root)
{Queue q;QInit(&q);if (root){QPush(&q, root);}while (!QEmpty(&q)){BTNode* front = QFront(&q);printf("%d ", front->data);QPop(&q);if (front->left)QPush(&q, front->left);if (front->right)QPush(&q, front->right);}printf("\n");QDestroty(&q);
}

2.7判断二叉树是否是完全二叉树及二叉树销毁

2.7.1判断二叉树是否是完全二叉树（BinaryTreeComplete）

这个是建立在层序遍历的基础上的，利用层序遍历，遍历到第一个NULL时，后面都不能为NULL才为完全二叉树，如果后面有一个不能为NULL，那就不是完全二叉树返回false。

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QInit(&q);if (root){QPush(&q, root);}while (!QEmpty(&q)){BTNode* front = QFront(&q);QPop(&q);if (front == NULL){break;}else{QPush(&q,front->left);QPush(&q,front->right);}}while (!QEmpty(&q)){BTNode* front = QFront(&q);QPop(&q);if (front != NULL){QDestroty(&q);return false;}}QDestroty(&q);return true;	
}

2.7.2二叉树销毁（TreeDestory）：

// 二叉树销毁
void TreeDestory(BTNode* root)
{if (root == NULL)return;TreeDestory(root->left);TreeDestory(root->right);free(root);}

3.完整代码：

3.1test.c文件(二叉树实现):

#include"Queue.h"
#include
#include
#include
#include
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyBTNode(BTDataType x)
{BTNode*newnode=(BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}
// 二叉树前序遍历
void PreOrder(BTNode* root)
{//assert(root);if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
// 二叉树节点个数
int TreeSize(BTNode* root)
{if (root == NULL)return 0;return TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 二叉树叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left+1 : right+1;
}
// 二叉树第k层节点个数
int TreeLevelSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1 )//当k==1时，刚好是第三层return 1;return TreeLevelSize(root->left, k - 1) + TreeLevelSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x) 
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* left = TreeFind(root->left,x);if (left)return left;BTNode* right = TreeFind(root->right, x);if (right)return right;return NULL;
}
//层序遍历
void LevelOrder(BTNode* root)
{Queue q;QInit(&q);if (root){QPush(&q, root);}while (!QEmpty(&q)){BTNode* front = QFront(&q);printf("%d ", front->data);QPop(&q);if (front->left)QPush(&q, front->left);if (front->right)QPush(&q, front->right);}printf("\n");QDestroty(&q);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QInit(&q);if (root){QPush(&q, root);}while (!QEmpty(&q)){BTNode* front = QFront(&q);QPop(&q);if (front == NULL){break;}else{QPush(&q,front->left);QPush(&q,front->right);}}while (!QEmpty(&q)){BTNode* front = QFront(&q);QPop(&q);if (front != NULL){QDestroty(&q);return false;}}QDestroty(&q);return true;	
}
// 二叉树销毁
void TreeDestory(BTNode* root)
{if (root == NULL)return;TreeDestory(root->left);TreeDestory(root->right);free(root);}
void test1()
{//构造二叉树BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);BTNode* n7 = BuyBTNode(7);n1->left = n2;//链接二叉树n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;n3->left = n7;printf("前序遍历顺序：");PreOrder(n1);printf("\n");printf("中序遍历顺序：");InOrder(n1);printf("\n");printf("后序遍历顺序：");PostOrder(n1);printf("\n");printf("Treesize:%d\n", TreeSize(n1));printf("TreeHeight:%d\n", TreeHeight(n1));printf("TreeLevelSize:%d\n", TreeLevelSize(n1,3));printf("TreeFind:%d\n", TreeFind(n1, 3)->data);LevelOrder(n1);printf("是否是完全二叉树：%d", BinaryTreeComplete(n1));TreeDestory(n1);n1 = NULL;
}
//void test2()
//{
//	BTNode* n1 = BuyBTNode(1);
//	BTNode* n2 = BuyBTNode(1);
//	BTNode* n3 = BuyBTNode(1);
//	BTNode* n4 = BuyBTNode(1);
//	BTNode* n5 = BuyBTNode(1);
//	//BTNode* n6 = BuyBTNode(1); 
//	BTNode* n7 = BuyBTNode(1);
//	n1->left = n2;
//	n1->right = n3;
//	n2->left = n4;
//	n2->right = n5;
//	n3->right = n7;
//}
int main()
{test1();//test2();return 0;
}

3.2Queue.h文件：

#pragma once
#include
#include
#include
#include
//前置声明
struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;
typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;
void QInit(Queue* pq);
void QDestroty(Queue* pq);
void QPush(Queue* pq, QDataType x);
void QPop(Queue* pq);
QDataType QFront(Queue* pq);
QDataType QBack(Queue* pq);
bool QEmpty(Queue* pq);
int QSize(Queue* pq);

3.3Queue.c文件：

#include"Queue.h"
void QInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}
void QDestroty(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);}pq->head = pq->tail = NULL;
}
void QPush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail==NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}
void QPop(Queue* pq)
{assert(pq);assert(!QEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = NULL;pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);del = NULL;}pq->size--;
}
QDataType QFront(Queue* pq)
{assert(pq);assert(!QEmpty(pq));return pq->head->data;
}
QDataType QBack(Queue* pq)
{assert(pq);assert(!QEmpty(pq));return pq->tail->data;
}
bool QEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}
int QSize(Queue* pq)
{assert(pq);return pq->size;
}