智能优化算法:协作搜索算法-附代码
智能优化算法:协作搜索算法
摘要:协作搜索算法( Cooperation search algorithm ,CSA)是 Zhong-kai Feng等 于 2021 年提出的一种新型元启发式优化算法 。 该算法受现代企业团队协作行为的启发,具有寻优能力强,收敛速度快的特点。
1.协作搜索算法
协作搜索算法主要包括4个阶段:团队建立,团队沟通,反思学习,内部竞争。
1.1 团队建立
在这一阶段,团队中的所有员工都是通过式(1)随机生成的。在评估所有解决方案的性能后,将从初始群中选择 M∈[1,I]\mathrm{M} \in[1, \mathrm{I}]M∈[1,I] 个领导者,以 形成外部精英集。
xi,jk=ϕ(x‾j,x‾j),i∈[1,I],j∈[1,J],k=1(1)\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}=\phi\left(\underline{\mathrm{x}}_{\mathrm{j}}, \overline{\mathrm{x}}_{\mathrm{j}}\right), \mathrm{i} \in[1, \mathrm{I}], \mathrm{j} \in[1, \mathrm{~J}], \mathrm{k}=1 \tag{1} xi,jk=ϕ(xj,xj),i∈[1,I],j∈[1, J],k=1(1)
其中, I是当前种群的解数量; xi,jk\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}xi,jk 是第 k\mathrm{k}k 次迭代中第 i\mathrm{i}i 个个体的第 j\mathrm{j}j 个位置; ϕ(L,U)\phi(\mathrm{L}, \mathrm{U})ϕ(L,U) 是在 [L,U][\mathrm{L}, \mathrm{U}][L,U] 范围内 生成均匀分布的随机数的函数。
1.2 团队沟通
每位员工都可以通过与董事长、董事会和监事会的领导交流信息来获得新的信息。如式(2)所示,团队 沟通过程包括三个部分: 董事长的知识 AAA 、董事会的集体知识 B\mathrm{B}B 和监事会的集体知识 C\mathrm{C}C 。董事长从董 事会中随机选出,模批轮换饥制,而董事会和监事会的所有成员在计算B和 C\mathrm{C}C 时被赋予相同的职位。
ui,jk+1=xi,jk+Ai,jk+Bi,jk+Ci,jk,i∈[1,I],j∈[1,J],k∈[1,K](2)\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}=\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}+\mathrm{A}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}+\mathrm{B}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}+\mathrm{C}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}, \mathrm{i} \in[1, \mathrm{I}], \mathrm{j} \in[1, \mathrm{~J}], \mathrm{k} \in[1, \mathrm{~K}] \tag{2} ui,jk+1=xi,jk+Ai,jk+Bi,jk+Ci,jk,i∈[1,I],j∈[1, J],k∈[1, K](2)
Ai,jk=log(1/ϕ(0,1))⋅(gBestind ,jk−xi,jk)(3)\mathrm{A}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}=\log (1 / \phi(0,1)) \cdot\left(\mathrm{gBest}_{\text {ind }, \mathrm{j}}^{\mathrm{k}}-\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}\right) \tag{3} Ai,jk=log(1/ϕ(0,1))⋅(gBestind ,jk−xi,jk)(3)
Bi,jk=α⋅ϕ(0,1)⋅[1M∑m=1MgBestm,jk−xi,jk](4)\mathrm{B}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}=\alpha \cdot \phi(0,1) \cdot\left[\frac{1}{\mathrm{M}} \sum_{\mathrm{m}=1}^{\mathrm{M}} \mathrm{gBest}_{\mathrm{m}, \mathrm{j}}^{\mathrm{k}}-\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}\right] \tag{4} Bi,jk=α⋅ϕ(0,1)⋅[M1m=1∑MgBestm,jk−xi,jk](4)
Ci,jk=β⋅ϕ(0,1)⋅[1I∑i=1IpBesti,jk−xi,jk](5)\mathrm{C}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}=\beta \cdot \phi(0,1) \cdot\left[\frac{1}{\mathrm{I}} \sum_{\mathrm{i}=1}^{\mathrm{I}} \mathrm{pBest}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}-\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}\right] \tag{5} Ci,jk=β⋅ϕ(0,1)⋅[I1i=1∑IpBesti,jk−xi,jk](5)
其中, ui,jk+1\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}ui,jk+1 是第 k+1\mathrm{k}+1k+1 次迭代中第 i\mathrm{i}i 个个体的第 j\mathrm{j}j 个值; pBesti,jk\mathrm{pBest}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}pBesti,jk 是第 k\mathrm{k}k 代第 i\mathrm{i}i 个个体最优解的第 j\mathrm{j}j 个值; 择的索引; Ai,jk\mathrm{A}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}Ai,jk 表示从外部精英集中随机选择的主席获得的知识; Bi,jk\mathrm{B}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}Bi,jk 和 Ci,jk\mathrm{C}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}Ci,jk 分别是从迄今为止发现的 M\mathrm{M}M 个全局最优解和 I\mathrm{I}I 个个体最优解中获得的平均知识; α\alphaα 和 β\betaβ 是调整 Bi,jk\mathrm{B}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}Bi,jk 和 Ci,jk\mathrm{C}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}}Ci,jk 影响程度的学习系数。
1.3 反思学习
除了向领导者学习外,员工还可以通过总结自己在相反方向上的经验来获得新知识,具体表达如下: ri,jk+1={ϕ(x‾j+x‾j−ui,jk+1,cj)if (∣ui,jk+1−cj∣<ϕ(0,1)⋅∣x‾j−x‾j∣)ϕ(x‾j,x‾j+x‾j−ui,jk+1)otherwise (7)\mathrm{r}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}= \begin{cases}\phi\left(\overline{\mathrm{x}}_{\mathrm{j}}+\underline{x}_{\mathrm{j}}-\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}, \mathrm{c}_{\mathrm{j}}\right) & \text { if }\left(\left|\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}-\mathrm{c}_{\mathrm{j}}\right|<\phi(0,1) \cdot\left|\overline{\mathrm{x}}_{\mathrm{j}}-\underline{\mathrm{x}}_{\mathrm{j}}\right|\right) \\ \phi\left(\underline{x}_{\mathrm{j}}, \overline{\mathrm{x}}_{\mathrm{j}}+\underline{\mathrm{x}}_{\mathrm{j}}-\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}\right) & \text { otherwise }\end{cases}\tag{7} ri,jk+1=⎩⎨⎧ϕ(xj+xj−ui,jk+1,cj)ϕ(xj,xj+xj−ui,jk+1) if (ui,jk+1−cj<ϕ(0,1)⋅xj−xj) otherwise (7) pi,jk+1={ϕ(cj,x‾j+x‾j−ui,jk+1)if (∣ui,jk+1−cj∣<ϕ(0,1)⋅∣x‾j−x‾j∣)ϕ(x‾j+x‾j−ui,jk+1,x‾j)otherwise (8)\mathrm{p}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}= \begin{cases}\phi\left(\mathrm{c}_{\mathrm{j}}, \overline{\mathrm{x}}_{\mathrm{j}}+\underline{x}_{\mathrm{j}}-\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}\right) & \text { if }\left(\left|\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}-\mathrm{c}_{\mathrm{j}}\right|<\phi(0,1) \cdot\left|\overline{\mathrm{x}}_{\mathrm{j}}-\underline{\mathrm{x}}_{\mathrm{j}}\right|\right) \\ \phi\left(\overline{\mathrm{x}}_{\mathrm{j}}+\underline{x}_{\mathrm{j}}-\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}, \overline{\mathrm{x}}_{\mathrm{j}}\right) & \text { otherwise }\end{cases}\tag{8} pi,jk+1=⎩⎨⎧ϕ(cj,xj+xj−ui,jk+1)ϕ(xj+xj−ui,jk+1,xj) if (ui,jk+1−cj<ϕ(0,1)⋅xj−xj) otherwise (8) cj=(x‾j+xj)⋅0.5(9)\mathrm{c}_{\mathrm{j}}=\left(\overline{\mathrm{x}}_{\mathrm{j}}+\mathrm{x}_{\mathrm{j}}\right) \cdot 0.5 \tag{9} cj=(xj+xj)⋅0.5(9) 团队通过确保所有表现较好的员工都能得到保护,逐步提升其市场竞争力,具体表示如下: F(x)=f(x)+∑e=1Ece1⋅max{ge(x),0}+∑f=1Fcf2⋅∣hf(x)∣(12)\mathrm{F}(\mathrm{x})=\mathrm{f}(\mathrm{x})+\sum_{\mathrm{e}=1}^{\mathrm{E}} \mathrm{c}_{\mathrm{e}}^1 \cdot \max \left\{\mathrm{g}_{\mathrm{e}}(\mathrm{x}), 0\right\}+\sum_{\mathrm{f}=1}^{\mathrm{F}} \mathrm{c}_{\mathrm{f}}^2 \cdot\left|\mathrm{h}_{\mathrm{f}}(\mathrm{x})\right| \tag{12} F(x)=f(x)+e=1∑Ece1⋅max{ge(x),0}+f=1∑Fcf2⋅∣hf(x)∣(12) 其中, xjx_jxj 是解 xxx 中的第 jjj 个值; ce1c_e^1ce1 是第 e\mathrm{e}e 个不等式约束的惩罚系数; cf2c_{\mathrm{f}}^2cf2 是第 f\mathrm{f}f 个不等式约束的惩罚系数。 [1] Zhong-kai Feng, Wen-jing Niu, Shuai Liu. Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems[J]. Applied Soft Computing Journal, 2021, 98: 106734.
vi,jk+1={ri,jk+1if (ui,jk+1≥cj)pi,jk+1if (ui,jk+11.4 内部竞争
xi,jk+1={ui,jk+1if (F(ui,jk+1)≤F(vi,jk+1))vi,jk+1if (F(ui,jk+1)>F(vi,jk+1)),i∈[1,I],j∈[1,J],k∈[1,K]\mathrm{x}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}=\left\{\begin{array}{ll} \mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1} & \text { if }\left(\mathrm{F}\left(\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}\right) \leq \mathrm{F}\left(\mathrm{v}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}\right)\right) \\ \mathrm{v}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1} & \text { if }\left(\mathrm{F}\left(\mathrm{u}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}\right)>\mathrm{F}\left(\mathrm{v}_{\mathrm{i}, \mathrm{j}}^{\mathrm{k}+1}\right)\right) \end{array}, \mathrm{i} \in[1, \mathrm{I}], \mathrm{j} \in[1, \mathrm{~J}], \mathrm{k} \in[1, \mathrm{~K}]\right. xi,jk+1=⎩⎨⎧ui,jk+1vi,jk+1 if (F(ui,jk+1)≤F(vi,jk+1)) if (F(ui,jk+1)>F(vi,jk+1)),i∈[1,I],j∈[1, J],k∈[1, K]
其中, F(x)\mathrm{F}(\mathrm{x})F(x) 是解 x\mathrm{x}x 的适应度值。为了有效地多重物理约束,首先通过式(11)将 x\mathrm{x}x 中的所有变量修改为 可行区域,然后使用式(12)中的征罚函数方法,通过将约束违反值合并到目标值 F(x)\mathrm{F}(\mathrm{x})F(x) 中来获得适应度 值 F(x)\mathrm{F}(\mathrm{x})F(x) 。然后,对于可行解,充分满足所有约束,使适应度值等于原始目标值;对于不可行解,约 束冲突值变为正值,因此适应度值大于目标值。这样,就可以将种群引导到尽可能多的可行搜索区域。
xj=max{min{x‾j,xj},x‾j}(11)\mathrm{x}_{\mathrm{j}}=\max \left\{\min \left\{\overline{\mathrm{x}}_{\mathrm{j}}, \mathrm{x}_{\mathrm{j}}\right\}, \underline{x}_{\mathrm{j}}\right\} \tag{11} xj=max{min{xj,xj},xj}(11)
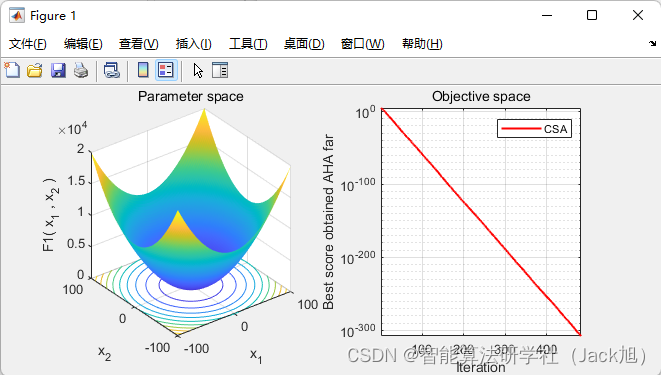
2.实验结果
3.参考文献
4.Matlab
5.Python
下一篇:ArrayList与顺序表(一)
