数学建模学习笔记-算法(线性规划模型)-上
目录
线性规划问题
线性规划的matlab标准形式
解析
目标函数
约束条件
使用matlab的linprog函数来进行求解
线性规划问题
数学规划:安排现有资源安排生产,以取得最大效益的问题。
线性规划:目标函数和约束条件均为线性函数
在一组线性约束条件的限制下,求线性目标函数最大或最小的问题。
可行解:满足约束条件的解就是可行解
最优解:使目标函数达到最值的可行解
可行域:所有可行解构成的集合,记为R
线性规划的matlab标准形式
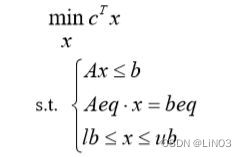
解析
为目标函数
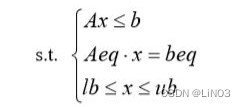
为约束条件
目标函数
c 为目标函数系数,列向量
例
目标函数:minz=2*x1+3*x2+5*x3minz是所求最小值
c就是[2,3,5]
如果求最大值需要把系数取负值
例
目标函数:maxz=2*x1+3*x2+5*x3maxz是所求最大值
但matlab的标准形式为求最小值,所以求最大值时需要取负数
c就是[-2,-3,-5]
在matlab中表示成
c=[-2,-3,-5]约束条件
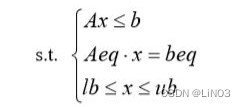
1.“s.t.”,指 subject to,受限制于...,所以s.t.所包含的就是他的约束条件
例
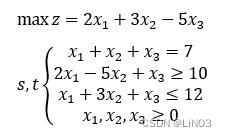
2.A为小于等于的系数矩阵,b为小于等于值列向量
那么小于等于的约束条件是
2*x1-5*x2+x3>=10
x1+3*x2+x3<=12
但matlab的标准形式为小于等于,所以第一个式子要两边取负数,变成小于等于就变成了
-2*x1+5*x2-x3<=-10
x1+3*x2+x3<=12
那么显而易见系数矩阵A就是
同理它所对应的值列向量b
那么在matlab中表示成
A=[-2,5,-1;1,3,1]
b=[-10,12]3.Aeq为等于的系数矩阵的系数矩阵
Beq为等于的值列向量
那么等于的约束条件是
x1+x2+x3=7
那么显而易见系数矩阵Aeq就是
同理它所对应的值列向量Beq
7
那么在matlab中表示成
Aeq=[1,1,1]
Beq=54.LB为x i 的下界,UB为上界
那么等于的约束条件是
x1,x2,x3>=0
没有上界所以 不需要ub
而下界lb则为3个0
那么在matlab中表示成
lb = [0;0;0]使用matlab的linprog函数来进行求解
[x,fval]=lingrog(c,A,b,Aeq,Beq,lb,ub)将其一个个带入
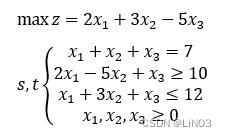
就可以写出
c = [-2;-3;5];
A = [-2 5 -1];
b = -10;
Aeq = [1 1 1];
beq = 7;
LB = [0;0;0];
[x,fval] = linprog(c,A,b,Aeq,beq,LB);
x 为最优解,
求最小值时
fval 为最优的目标函数值
求最大值时
-fval 为最优的目标函数值
总结
x 为最优解, fval 为最优的目标函数值
c 为目标函数系数,列向量
A为小于等于的系数矩阵,b为小于等于值列向量
Aeq,Beq为等于约束,含义同上
LB为x i xi x i 的下界,UB为上界,列向量
注意后面的参数可以省略,中间如果有条件用不到,需要用[]占位将以上字母按照matlab标准形式带入[x,fval]=lingrog(c,A,b,Aeq,Beq,lb,ub)
注:遇到非典型的线性规划可以用数学知识,尝试转化为线性规划问题
