螺旋矩阵题目：

leetcode54，59，885，2326

leetcode54

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

class Solution {
public:vector spiralOrder(vector>& matrix) {int n=matrix.size();//n行int m=matrix[0].size();//m列vectorvec;int t=0;int b=n-1;int l=0;int r=m-1;int count=n*m;while(count>=1){for(int i=l;i<=r && count>=1;i++){vec.push_back(matrix[t][i]);count--;}t++;for(int i=t;i<=b &&count>=1;i++){vec.push_back(matrix[i][r]);count--;}r--;for(int i=r;i>=l && count>=1;i--){vec.push_back(matrix[b][i]);count--;}b--;for(int i=b;i>=t && count>=1;i--){vec.push_back(matrix[i][l]);count--;}l++;    }return vec;}
};

leetcode59

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
给你一个正整数 n ，生成一个包含 1 到 n*n所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

class Solution {
public:vector> generateMatrix(int n) {int t = 0;      // top上边界int b = n-1;    // bottom下边界int l = 0;      // left左边界int r = n-1;    // right右边界vector>vec(n,vector(n));int m=1;while(m<=n*n){// for(l;l<=r;l++;i++){vec[t][l]=i;} //这样写l会随着自增改变// t++;// for(t;t<=b;t++;i++){vec[t][l]=i;}//i与左右上下边界的移动无关，只是一个标记变量for(int i=l;i<=r;i++,m++){vec[t][i]=m;}t++;for(int i=t;i<=b;i++,m++){vec[i][r]=m;}r--;for(int i=r;i>=l;i--,m++){vec[b][i]=m;}b--;for(int i=b;i>=t;i--,m++){vec[i][l]=m;}l++;}return vec;}
};

leetcode 885. 螺旋矩阵 III

输入：rows = 1, cols = 4, rStart = 0, cStart = 0
输出：[[0,0],[0,1],[0,2],[0,3]]

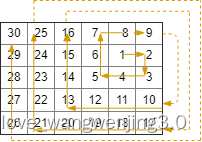
输入：rows = 5, cols = 6, rStart = 1, cStart = 4
输出：[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

class Solution {
public:vector> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {vector>vec;int count=rows*cols;int step=1;while(count>=1){int right=cStart+step;//右边界 往右for(cStart;cStartif(rStart>=0 && rStart=0 && cStartvec.push_back({rStart,cStart});count--;}}int bottom=rStart+step;///往下for(rStart;rStartif(rStart>=0 && rStart=0 && cStartvec.push_back({rStart,cStart});count--;}}step++;//增加步长int left=cStart-step;//往左for(cStart;cStart>left;cStart--){if(rStart>=0 && rStart=0 && cStartvec.push_back({rStart,cStart});count--;}}int top=rStart-step;///往上for(rStart;rStart>top;rStart--){if(rStart>=0 && rStart=0 && cStartvec.push_back({rStart,cStart});count--;}} step++;//最后还要step++增加步长}return vec;}
};

leetcode2326. 螺旋矩阵 IV

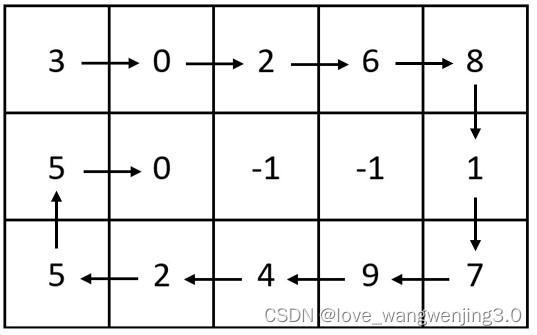
输入：m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
输出：[[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
解释：上图展示了链表中的整数在矩阵中是如何排布的。
注意，矩阵中剩下的空格用 -1 填充。
给你两个整数：m 和 n ，表示矩阵的维数。
另给你一个整数链表的头节点 head 。
请你生成一个大小为 m x n 的螺旋矩阵，矩阵包含链表中的所有整数。链表中的整数从矩阵 左上角 开始、顺时针 按 螺旋 顺序填充。如果还存在剩余的空格，则用 -1 填充。返回生成的矩阵。

struct ListNode {int val;ListNode *next;ListNode() : val(0), next(nullptr) {}ListNode(int x) : val(x), next(nullptr) {}ListNode(int x, ListNode *next) : val(x), next(next) {}};
class Solution {
public:vector> spiralMatrix(int m, int n, ListNode* head) {ListNode* cur=head;int count=m*n;int t=0;int b=m-1;int l=0;int r=n-1;bool flag=false;vector>vec(m,vector(n,-1));while(count>=1){for(int i=l;i<=r;i++){if(cur==nullptr){flag=true;break;}vec[t][i]=cur->val;cur=cur->next;count--;       }if(flag){break;}t++;for(int i=t;i<=b;i++){if(cur==nullptr){flag=true;break;}vec[i][r]=cur->val;cur=cur->next;count--;}if(flag){break;}r--;for(int i=r;i>=l;i--){if(cur==nullptr){flag=true;break;}vec[b][i]=cur->val;cur=cur->next;count--;}if(flag){break;}b--;for(int i=b;i>=t;i--){if(cur==nullptr){flag=true;break;}vec[i][l]=cur->val;cur=cur->next;count--;}if(flag){break;}l++;}return vec;}
};