作者：billy
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

简介

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。十大排序算法用一张图概括：

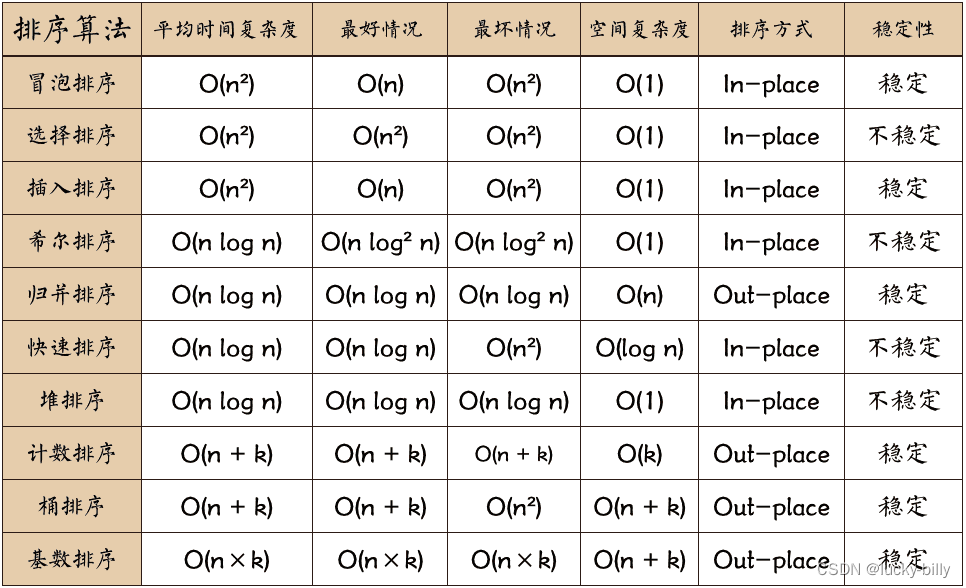
一. 冒泡排序

冒泡排序（Bubble Sort）是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。冒泡排序还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用

1. 算法步骤

• 1）比较相邻的元素。如果第一个比第二个大，就交换两个的位置
• 2）对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数
• 3）针对所有的元素重复以上的步骤，除了最后一个
• 4）持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较

2. 代码

void BSortMethod::bubbleSort(int *vec, int len)
{// 每次遍历找到最大的数放在最右边，最后一个数不用比较，所以一共进行 len - 1 次遍历for ( int i = 1; i < len; ++i ){for ( int j = 0; j < len - i; ++j ){if ( vec[j] > vec[j+1] ) {int temp = vec[j];vec[j] = vec[j+1];vec[j+1] = temp;}}}
}

3. 效果展示

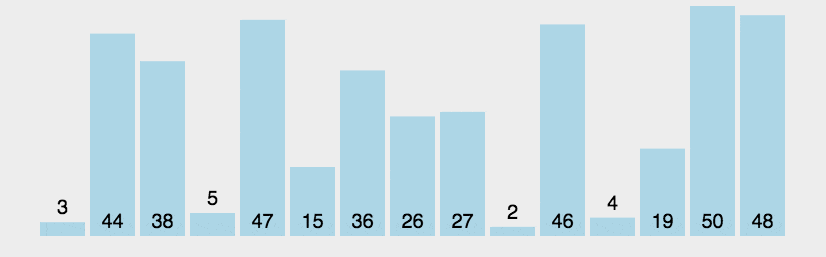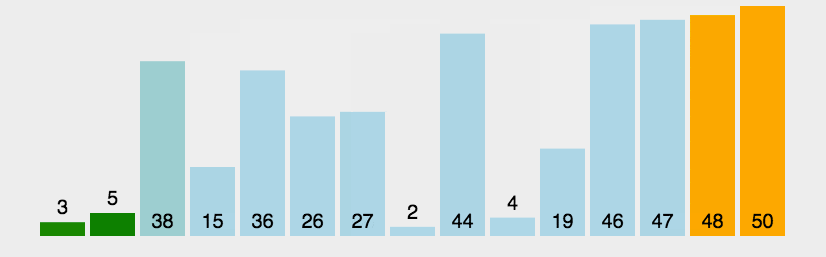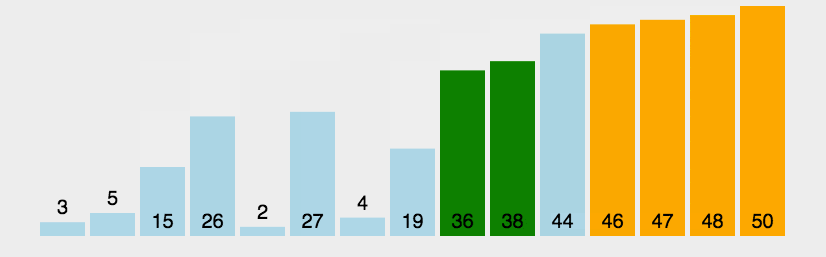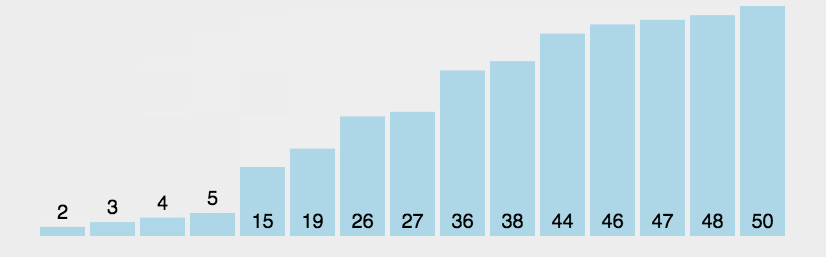
二. 选择排序

选择排序（Selection Sort）是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧

1. 算法步骤

• 1）首先在未排序的序列中找到最小或最大的元素，存放到排序序列的起始位置
• 2）再从剩余未排序元素中继续寻找最小或最大的元素，然后放到已排序序列的末尾
• 3）重复第二步，直到所有元素均排序完毕

2. 代码

void BSortMethod::selectionSort(int *vec, int len)
{for ( int i = 0; i < len - 1; ++i ){int minIndex = i;// 每次遍历找到最小值的索引for ( int j = i + 1; j < len; ++j ){if ( vec[j] < vec[minIndex] ) {minIndex = j;}}// 把最小值放在有序序列的最后if ( minIndex != i ) {int temp = vec[minIndex];vec[minIndex] = vec[i];vec[i] = temp;}}
}

3. 效果展示

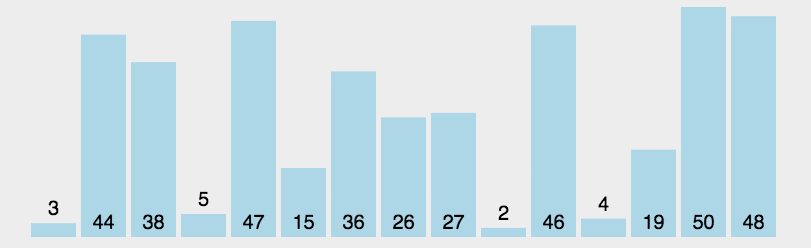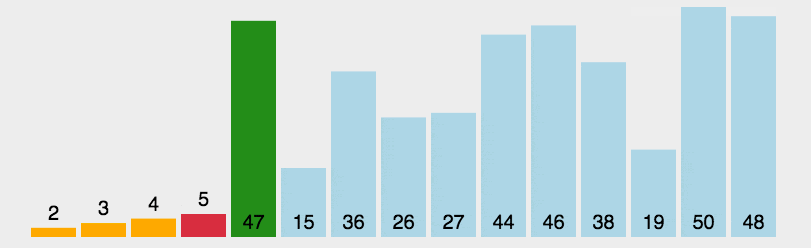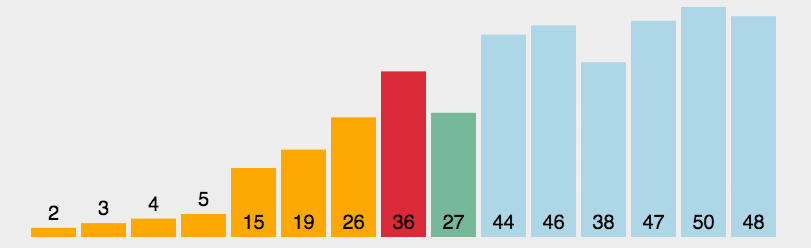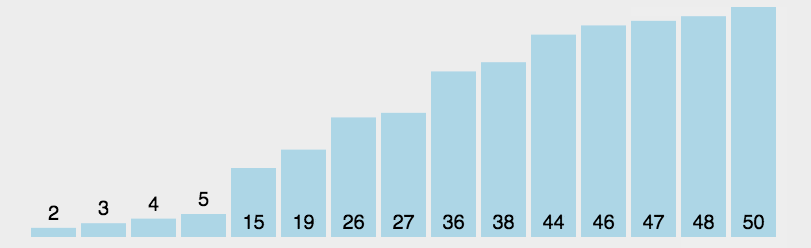
三. 插入排序

插入排序（Insertion Sort）的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

1. 算法步骤

• 1）把待排序序列的第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列
• 2）从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面

2. 代码

void BSortMethod::insertionSort(int *vec, int len)
{for ( int i = 0; i < len; ++i ){int preIndex = i - 1;int currentValue = vec[i];// 从后往前遍历有序列表，直到找到比当前数值小或者相等的数的索引，我们在这个索引后插入 currentValuewhile ( preIndex >= 0 && vec[preIndex] > currentValue ){vec[preIndex + 1] = vec[preIndex];preIndex--;}vec[preIndex+1] = currentValue;}
}

3. 效果展示

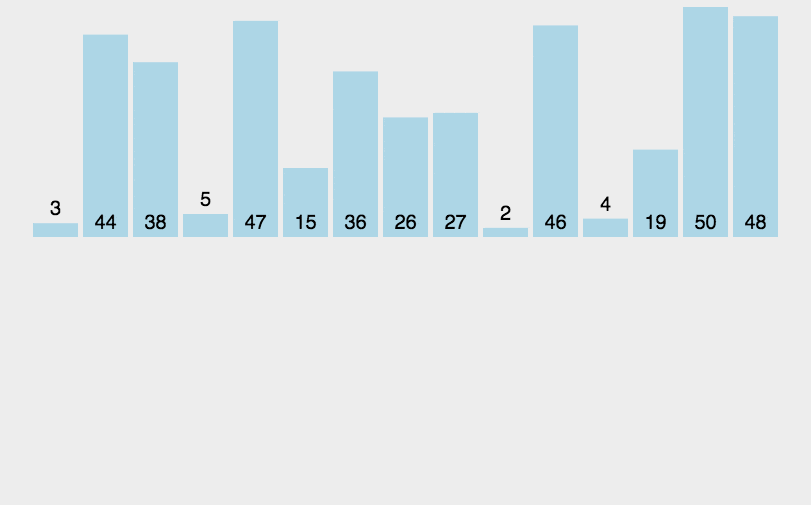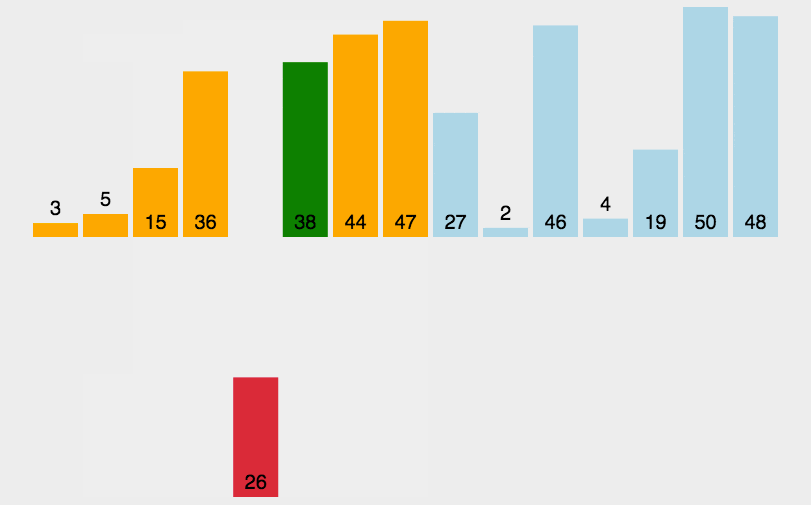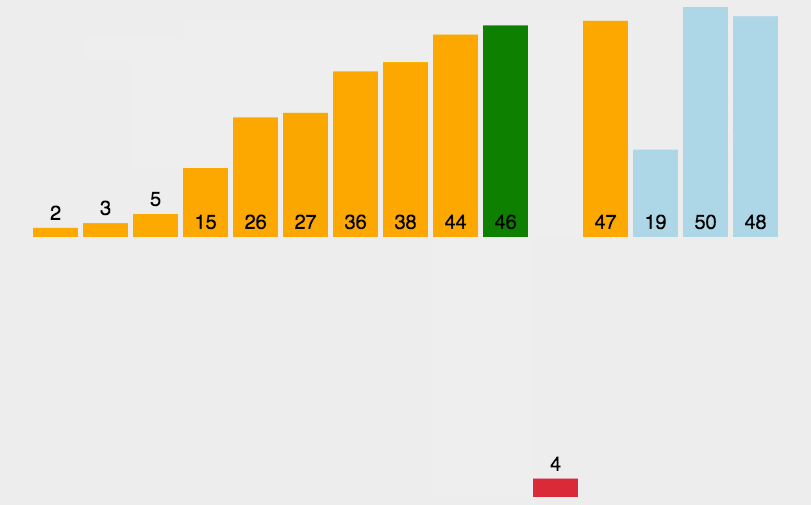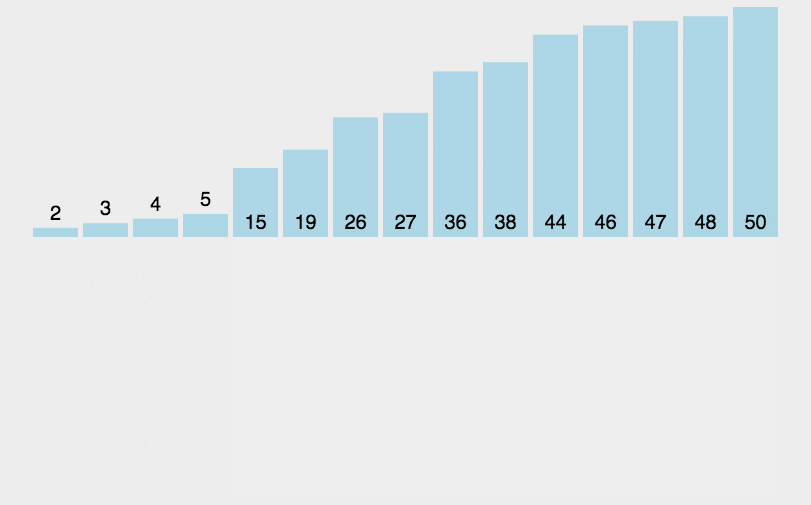
四. 希尔排序

希尔排序（Shell Sort），也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；
• 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位；

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序

1. 算法步骤

• 1）选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1
• 2）按增量序列个数 k，对序列进行 k 次排序
• 3）每次排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度

这是博主网上找的图片，更方便理解递减增量排序的流程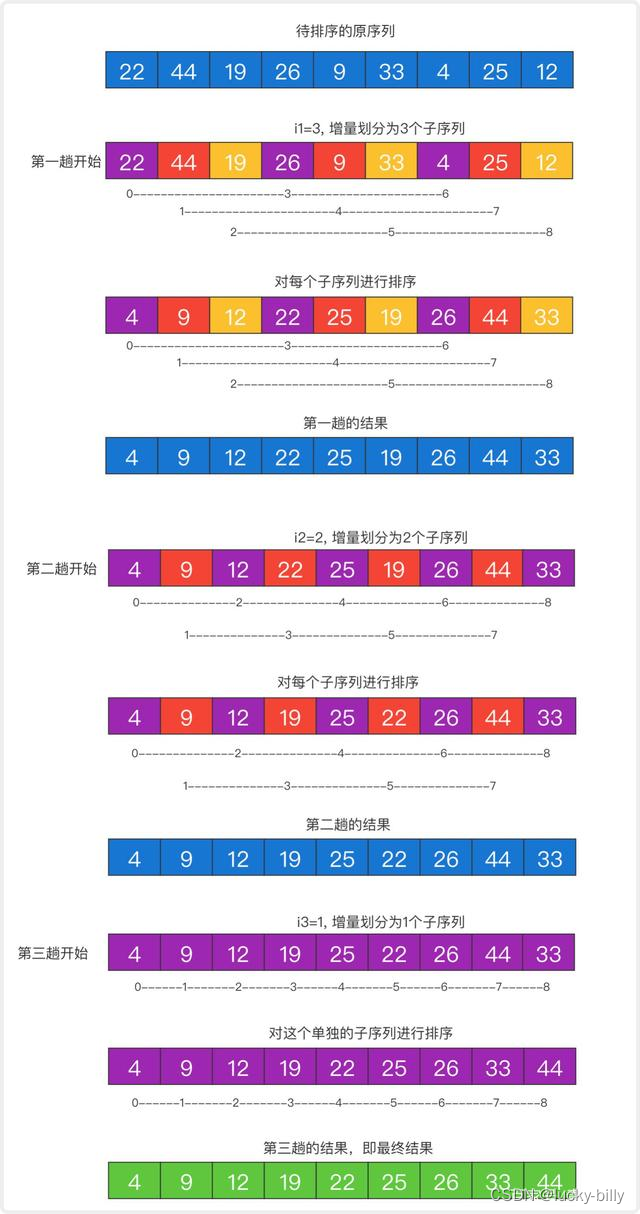

2. 代码

void BSortMethod::shellSort(int *vec, int len)
{// 初始增量 gap = len / 2，逐渐缩小增量 gap = gap / 2 直到变为 1for ( int gap = len / 2; gap >=1; gap = gap / 2 ){// 每一组进行排序for ( int i = gap; i < len; ++i ){int temp = vec[i];int j = i - gap;while ( j >= 0 && vec[j] > temp ){vec[j+gap] = vec[j];j -= gap;}vec[j+gap] = temp;}}
}

五. 归并排序

归并排序（Merge Sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

• 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
• 自下而上的迭代；

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间

1. 算法步骤

• 1）申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
• 2）设定两个指针，最初位置分别为两个已经排序序列的起始位置
• 3）比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
• 4）重复步骤 3 直到某一指针达到序列尾
• 5）将另一序列剩下的所有元素直接复制到合并序列尾

2. 代码

void BSortMethod::merge(int *vec, int len)
{int mid = len / 2;              // mid将数组从中间分割int *arr = new int[len];        // 临时数组（额外的内存空间）int s = 0;                      // 临时数组的起始位置int first = 0, second = mid;    // 两个数组的起始位置while ( first < mid && second < len ){// 比较大小if ( vec[first] <= vec[second] ) {arr[s++] = vec[first++];} else {arr[s++] = vec[second++];}}// 将剩余项复制到临时数组中while ( first < mid ){arr[s++] = vec[first++];}while ( second < len ){arr[s++] = vec[second++];}// 临时数组复制到原数组for (int i = 0; i < len; ++i){vec[i] = arr[i];}// 内存释放delete []arr;
}void BSortMethod::mergeSort(int *vec, int len)
{// 递归出口if ( len < 2 ) {return;}mergeSort(vec, len / 2);                    // 对前半部分进行归并排序mergeSort(vec + len / 2, len - len / 2);    // 对后半部分进行归并排序merge(vec, len);                            // 归并两部分
}

3. 效果展示

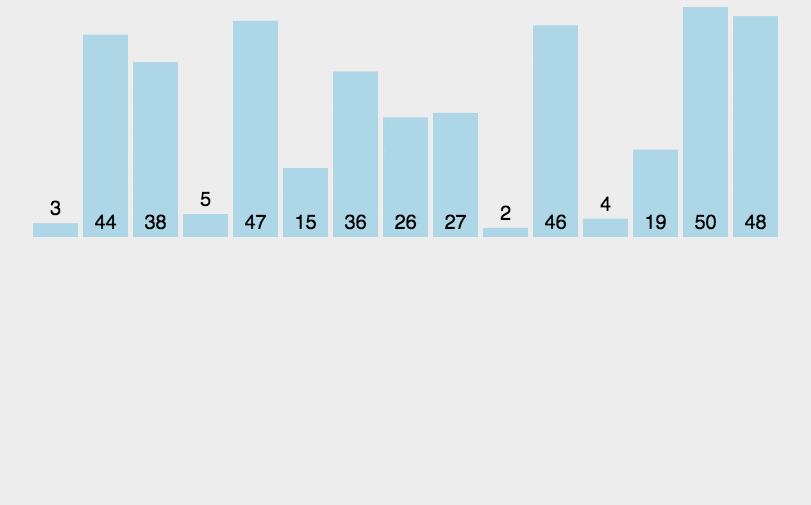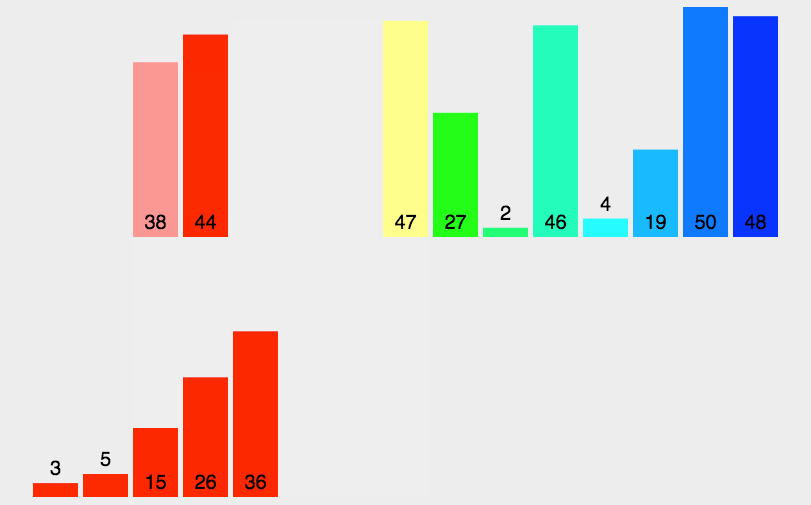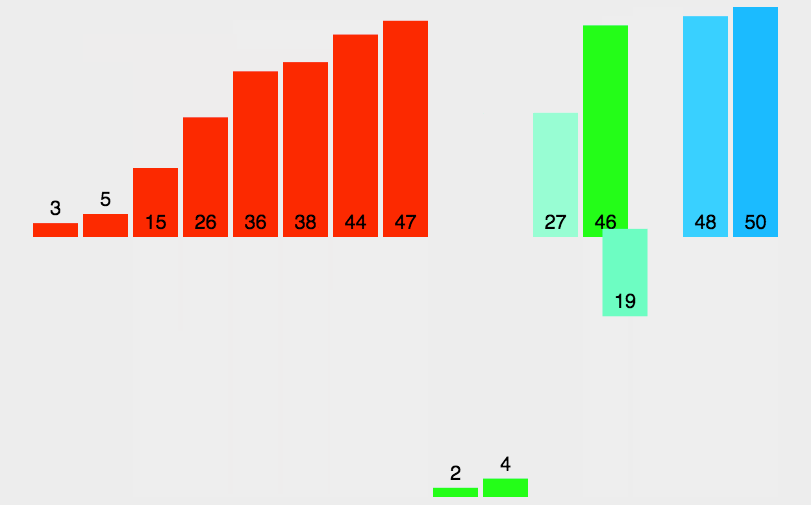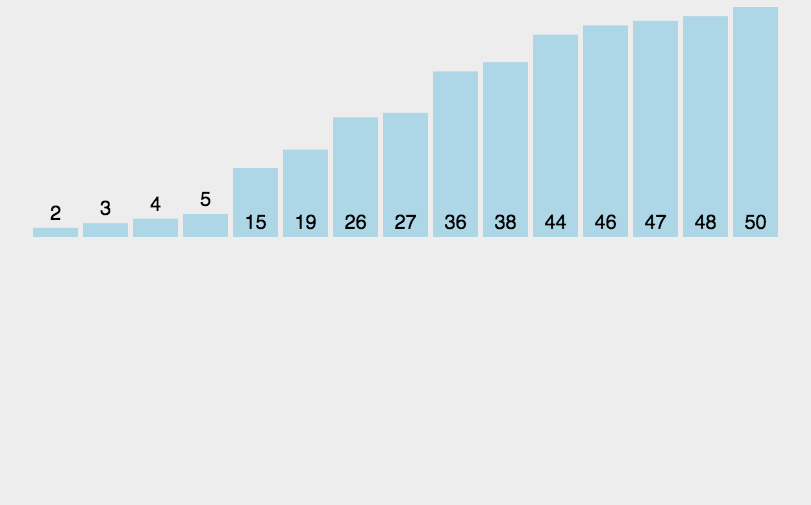
六. 快速排序

快速排序（Quick Sort）是由东尼·霍尔所发展的一种排序算法。速排序又是一种分而治之思想在排序算法上的典型应用。它的基本思想是通过一组排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据小，然后再按此方法对这两部分数据进行快速排序，整个排序过程可以递归进行，以此使所有数据变成有序序列

1. 算法步骤

• 1）从数列中挑出一个元素，称为 “基准”
• 2）重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作
• 3）递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去

2. 代码

void BSortMethod::swap(int *vec, int i, int j)
{int temp = vec[i];vec[i] = vec[j];vec[j] = temp;
}int BSortMethod::partition(int *vec, int left, int right)
{int pivot = left;int index = pivot + 1;int i = index;while ( i <= right ){if ( vec[i] < vec[pivot] ) {swap(vec, i, index);index += 1;}i += 1;}swap(vec, pivot, index - 1);// 返回最终划分完成后基准元素所在的位置return index - 1;
}void BSortMethod::quickSort(int *vec, int left, int right)
{if ( left < right ) {int mid = partition(vec, left, right);quickSort(vec, left, mid - 1);quickSort(vec, mid + 1, right);}
}

3. 效果展示

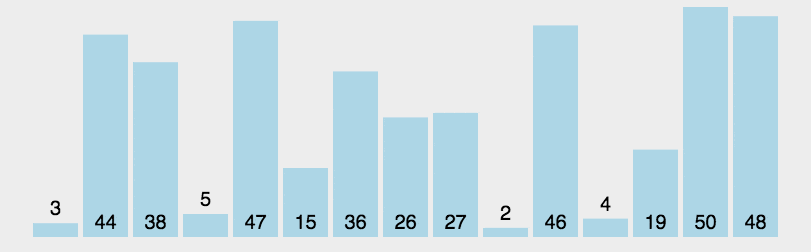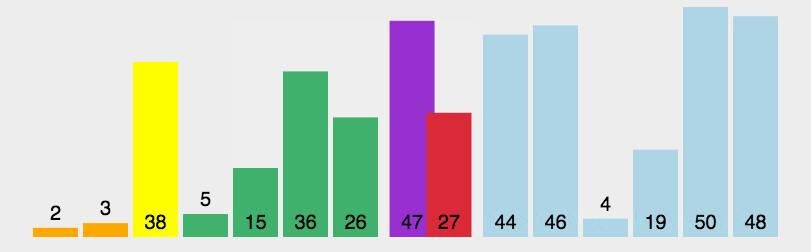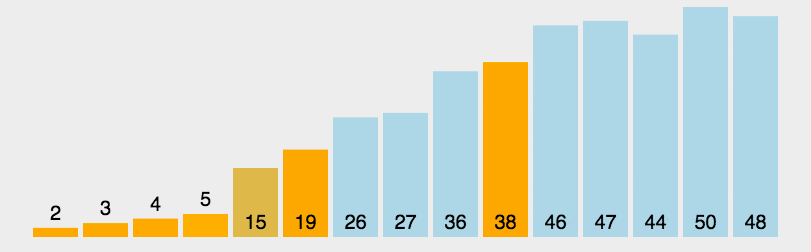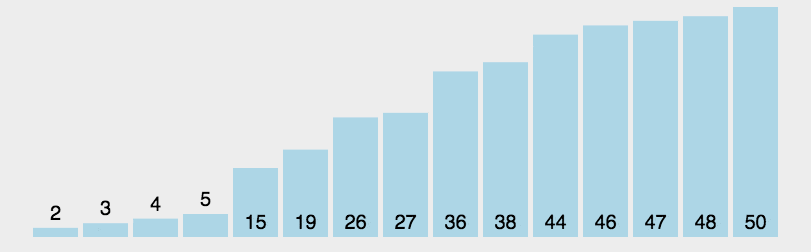
七. 堆排序

堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

• 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
• 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)

1. 算法步骤

• 1）创建一个堆 H[0……n-1]
• 2）把堆首（最大值）和堆尾互换
• 3）把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置
• 4）重复步骤 2，直到堆的尺寸为 1

2. 代码

void BSortMethod::heapify(int *vec, int i, int len)
{int left = i * 2 + 1;int right = i * 2 + 2;int largest = i;if ( left < len && vec[left] > vec[largest] ) {largest = left;}if ( right < len && vec[right] > vec[largest] ) {largest = right;}if ( largest != i ) {swap(vec, i, largest);heapify(vec, largest, len);}
}void BSortMethod::heapSort(int *vec, int len)
{// 从最后一个非叶子节点开始向上遍历，创建堆for ( int i = len / 2 - 1; i >= 0; i-- ){heapify(vec, i, len);}for ( int j = len - 1; j > 0; j-- ){swap(vec, 0, j);heapify(vec, 0, j);}
}

3. 效果展示

八. 计数排序

计数排序（Counting Sort）的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数

1. 算法步骤

• 1）找出待排序的数组中最大元素
• 2）统计数组中每个值为 i 的元素出现的次数，存入计数数组C的第 i-1 项
• 3）遍历计数数组C，将统计好的元素取出来放回原始数组

2. 代码

void BSortMethod::countingSort(int *vec, int len)
{if ( len <= 0 ) {return;}// 找到数组最大值int max = vec[0];for ( int i = 1; i < len; ++i ){if ( vec[i] > max ) {max = vec[i];}}// 根据找到的最大值来确定统计数组的长度int arrayLen = max + 1;// 动态申请内存，并初始化为 0int *array = new int[arrayLen] {0};// 遍历数组，填充统计数组（把原数组中的数据变为统计数组的索引，值都是1）for ( int j = 0; j < len; ++j ){array[vec[j]]++;}int index = 0;for ( int k = 0; k < arrayLen; ++k ){// 遍历统计数组，再把排序后的索引变回数值存在原来数组中while ( array[k] > 0 ){vec[index++] = k;array[k]--;}}// 释放内存delete []array;
}

3. 效果展示

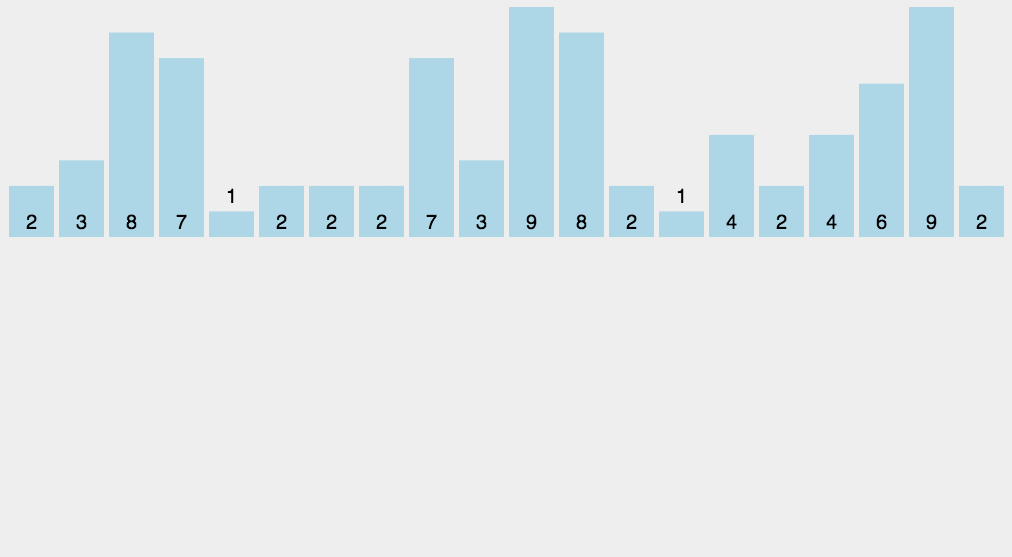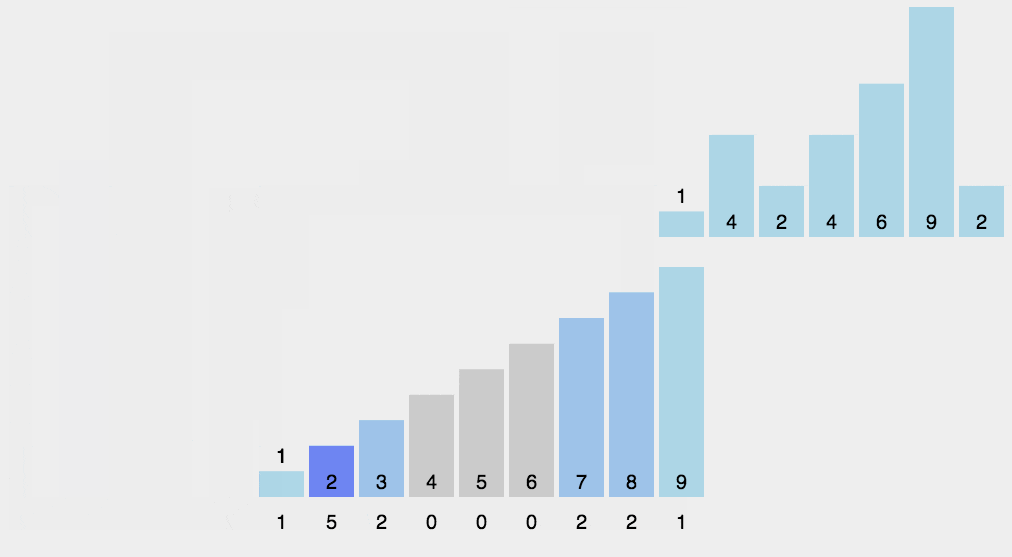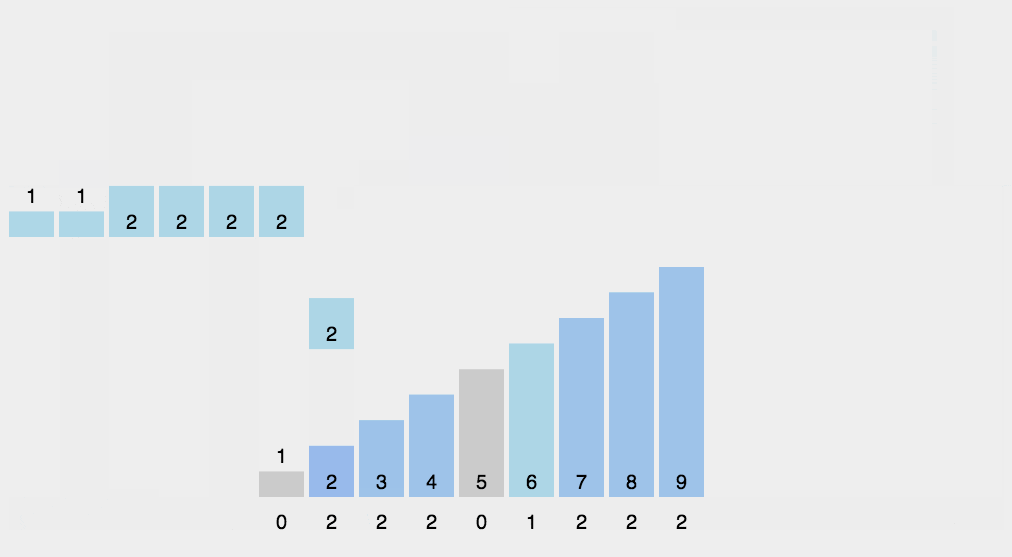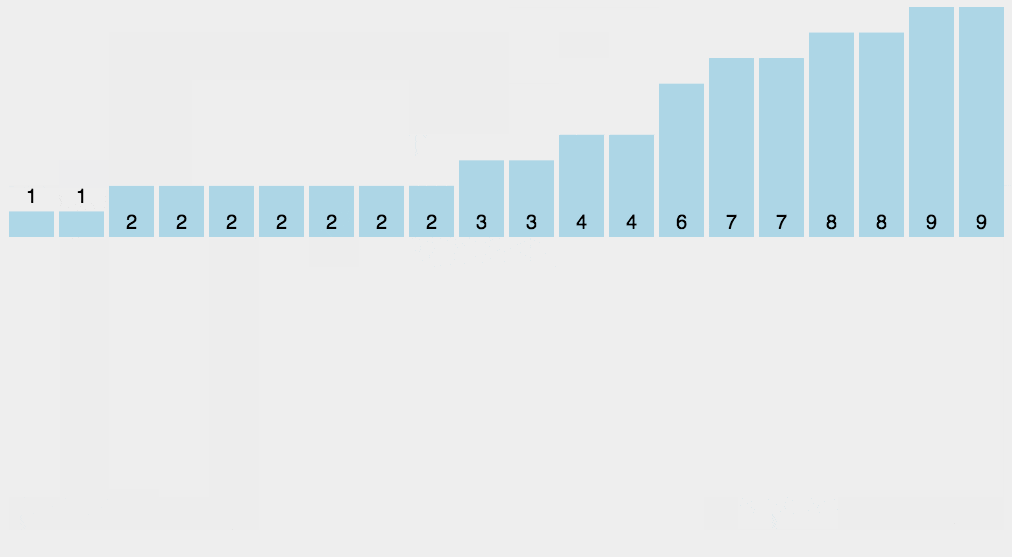
九. 桶排序

桶排序（Bucket Sort）是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：在额外空间充足的情况下，尽量增大桶的数量使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要

• 什么时候最快：当输入的数据可以均匀的分配到每一个桶中
• 什么时候最慢：当输入的数据被分配到了同一个桶中

1. 算法步骤

• 1）设置一个定量的数组当作空桶
• 2）遍历序列，并将元素一个个放到对应的桶中
• 3）对每个不是空的桶进行排序
• 4）从不是空的桶里把元素再放回原来的序列中

2. 代码

// 方法一
void BSortMethod::bucketSort(int *vec, int len)
{if ( len <= 0 ) {return;}// 找到数组最大值int max = vec[0];for ( int i = 1; i < len; ++i ){if ( vec[i] > max ) {max = vec[i];}}// 设置10个桶const int bucketNum = 10;// 定义二维数组std::vector buckets[bucketNum];// 计算桶的最大尺寸int bucketSize = 1;while (max) {max /= 10;bucketSize *= 10;}bucketSize /= 10;// 数据存入桶中for ( int i = 0; i < len; ++i ){// 定义元素存放的桶号int index = vec[i] / bucketSize;buckets[index].push_back(vec[i]);// 对该桶使用插入排序for ( int j = int(buckets[index].size()) - 1; j > 0; --j ){if ( buckets[index][j] < buckets[index][j-1] ) {int temp = buckets[index][j];buckets[index][j] = buckets[index][j-1];buckets[index][j-1] = temp;}}}// 顺序访问桶，得到有序数组for ( int i = 0, k = 0; i < bucketNum; ++i ){for ( int j = 0; j < int(buckets[i].size()); ++j ){vec[k++] = buckets[i][j];}}
}// 方法二
void BSortMethod::bucketSort2(int *vec, int len)
{if ( len <= 0 ) {return;}// 找到数组最大值，最小值int min = vec[0];int max = vec[0];for ( int i = 1; i < len; ++i){if ( vec[i] < min ) min = vec[i];if ( vec[i] > max ) max = vec[i];}// 桶的大小int bucketNum = (max - min) / len + 1;// 二维数组动态分配内存int **buckets = new int* [bucketNum];for ( int i = 0; i < bucketNum; ++i ){buckets[i] = new int[bucketNum] {0};}// 动态分配内存，存储每个桶的元素个数int *array = new int[bucketNum] {0};// 数据存入桶中for ( int i = 0; i < len; ++i ){// 定义元素存放的桶号int index = (vec[i] - min) / len;// 参考计数排序，填充统计数组buckets[index][array[index]++] = vec[i];}int index = 0;for ( int i = 0; i < bucketNum; ++i ){// 使用快速排序quickSort(buckets[i], 0, array[i] - 1);cout << i << "号桶的元素个数：" << array[i] << endl;// 遍历桶中元素，依次存入原数组for ( int j = 0; j < array[i]; ++j ){vec[index++] = buckets[i][j];}}// 释放内存delete[] buckets;delete[] array;
}

十. 基数排序

基数排序（Radix Sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数

1. 基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；
• 基数排序：根据键值的每位数字来分配桶；

2. 代码

void BSortMethod::radixSort(int *vec, int len)
{if ( len <= 0 ) {return;}// 找到数组最大值int max = vec[0];for ( int i = 1; i < len; ++i ){if ( vec[i] > max ) {max = vec[i];}}// 计算最大值的位数int maxBit = 1;while ( max > 10 * maxBit ){maxBit++;}for ( int k = 0; k < maxBit; ++k ){// 定义桶（二维数组）std::vector> bucket;for ( int i = 0; i < 10; ++i ){std::vector temp;bucket.push_back(temp);}// 对每一位进行排序for ( int i = 0; i < len; ++i ){// 得到每位的基数int radix = int((vec[i] / (int)pow(10, k)) % 10);// 将对应的数组元素添加到相应位基数的桶中bucket[radix].push_back(vec[i]);}int index = 0;for ( int i = 0; i < 10; ++i ){// 计算桶的元素个数int size = (int)bucket[i].size();if ( size != 0 ) {// 桶不为空时，将桶中每个元素放回到数组中for ( int j = 0; j < size; ++j ){vec[index++] = bucket[i][j];}}}}
}

3. 结果展示

函数调用

#include "bsortmethod.h"
#include "iostream"
using namespace std;int main()
{int vec[15] = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};int len = sizeof(vec) / sizeof(*vec);BSortMethod sortM;
//    sortM.bubbleSort(vec, len);		// 冒泡排序
//    sortM.selectionSort(vec, len);		// 选择排序
//    sortM.insertionSort(vec, len);	        // 插入排序
//    sortM.shellSort(vec, len);		// 希尔排序
//    sortM.mergeSort(vec, len);		// 归并排序
//    sortM.quickSort(vec, 0, len-1);		// 快速排序
//    sortM.heapSort(vec, len);			// 堆排序
//    sortM.countingSort(vec, len);		// 计数排序
//    sortM.bucketSort(vec, len);		// 桶排序1
//    sortM.bucketSort2(vec, len);		// 桶排序2sortM.radixSort(vec, len);			// 基数排序for(int i = 0; i < 15; ++i)cout << vec[i] << " ";cout << endl;
}

Github 代码

源代码下载