题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

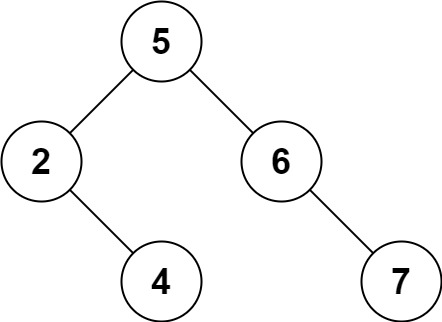
示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

解题思路

二叉搜索树有以下性质：

• 左子树的所有节点（如果有）的值均小于当前节点的值；
• 右子树的所有节点（如果有）的值均大于当前节点的值；
• 左子树和右子树均为二叉搜索树。

二叉搜索树的题目往往可以用递归来解决。此题要求删除二叉树的节点，函数 deleteNode 的输入是二叉树的根节点root 和一个整数 key\textit{key}key，输出是删除值为 key 的节点后的二叉树，并保持二叉树的有序性。可以按照以下情况分类讨论：

• root 为空，代表未搜索到值为 key 的节点，返回空。
• root.val>key，表示值为key 的节点可能存在于root 的左子树中，需要递归地在 root.left调用 deleteNode，并返回 root。
• root.val
• root.val=key，root即为要删除的节点。此时要做的是删除 root，并将它的子树合并成一棵子树，保持有序性，并返回根节点。根据 root 的子树情况分成以下情况讨论：

1. root 为叶子节点，没有子树。此时可以直接将它删除，即返回空。
2. root 只有左子树，没有右子树。此时可以将它的左子树作为新的子树，返回它的左子节点。
3. root只有右子树，没有左子树。此时可以将它的右子树作为新的子树，返回它的右子节点。
4. root 有左右子树，这时可以将 root的后继节点（比 root大的最小节点，即它的右子树中的最小节点，记为 successor）作为新的根节点替代 root，并将 successor从 root的右子树中删除，使得在保持有序性的情况下合并左右子树。 简单证明，successor 位于 root 的右子树中，因此大于 root 的所有左子节点；successor是 root的右子树中的最小节点，因此小于 root 的右子树中的其他节点。以上两点保持了新子树的有序性。 在代码实现上，我们可以先寻找 successor，再删除它。successor 是 root的右子树中的最小节点，可以先找到 root的右子节点，再不停地往左子节点寻找，直到找到一个不存在左子节点的节点，这个节点即为 successor。然后递归地在 root.right 调用 deleteNode来删除 successor。因为 successor没有左子节点，因此这一步递归调用不会再次步入这一种情况。然后将 successor更新为新的 root并返回。

代码实现

class Solution {public TreeNode deleteNode(TreeNode root, int key) {if (root == null) {return null;}if (root.val > key) {root.left = deleteNode(root.left, key);return root;}if (root.val < key) {root.right = deleteNode(root.right, key);return root;}if (root.val == key) {if (root.left == null && root.right == null) {return null;}if (root.right == null) {return root.left;}if (root.left == null) {return root.right;}TreeNode successor = root.right;while (successor.left != null) {successor = successor.left;}root.right = deleteNode(root.right, successor.val);successor.right = root.right;successor.left = root.left;return successor;}return root;}
}