目录

排序算法介绍

快速排序

算法流程

算法实现

python

C++

快排为什么快

算法优化

基准数优化

python

C++

尾递归优化

python

C++

排序算法介绍

《Hello算法》是GitHub上一个开源书籍，对新手友好，有大量的动态图，很适合算法初学者自主学习入门。而我则是正式学习算法，以这本书为参考，写写笔记，有错误的地方还请指正，下面我会用python和C++实现其中的实例

排序介绍：排序简介 - Hello 算法 (hello-algo.com)

这里有更详细的介绍。 

快速排序

Quick Sort是一种基于“分治思想”的排序算法，速度快、应用广。

快速排序的核心操作为“哨兵划分”，其目标是：选取数组某个元素为 基准数 ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

1.   以数组最左端元素作为基准数，初始化两个指针 i , j 指向数组两端；
2. 设置一个循环，每轮中使用 i / j 分别寻找首个比基准数大 / 小的元素，并交换此两元素；
3. 不断循环步骤 2. ，直至 i , j 相遇时跳出，最终把基准数交换至两个子数组的分界线；  

“哨兵划分”执行完毕后，原数组被划分成两个部分，即 左子数组 和 右子数组 ，且满足 左子数组任意元素 < 基准数 < 右子数组任意元素。因此，接下来我们只需要排序两个子数组即可。

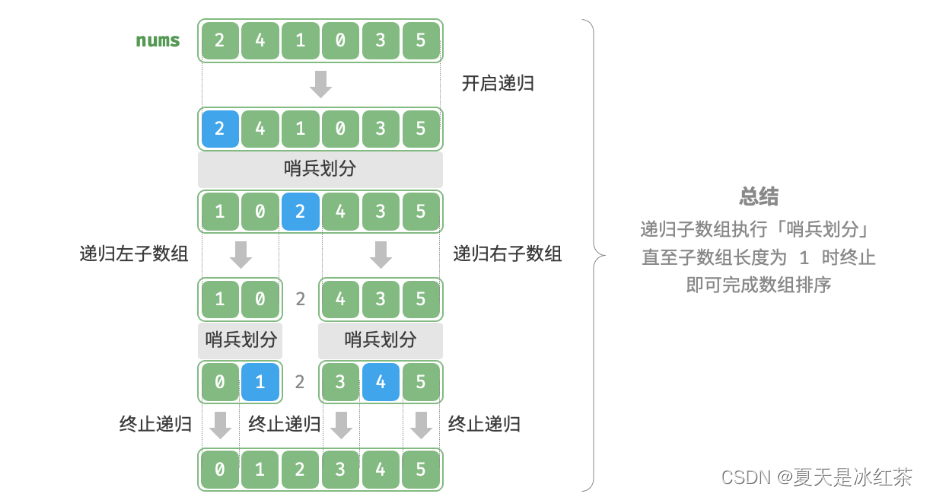
算法流程

1、首先对数组执行一次哨兵划分，得到待排列的左子数组与右子数组。

2、接下来，对这两个子数组分别进行递归执行哨兵划分

3、直至子数长度为1时终止递归，即可完成对整个数组的排列。

算法实现

接下来将以python与C++为例。

python

def quick_sort(self,nums,left,right):# 当子数长度为1时终止递归if left >= right:return# 哨兵划分pivot = self.partition(nums,left,right)# 递归左子数组、右子数组self.quick_sort(nums,left,pivot-1)self.quick_sort(nums,pivot+1,right)

C++

void quickSort(vector& nums, int left, int right) {// 子数组长度为 1 时终止递归if (left >= right)return;// 哨兵划分int pivot = partition(nums, left, right);// 递归左子数组、右子数组quickSort(nums, left, pivot - 1);quickSort(nums, pivot + 1, right);
}

快排为什么快

从命名能够看出，快速排序一定在效率方面有优势。快速排序的平均时间复杂度虽然与归并排序和堆排序一致，但实际 效率更高 ，这是因为：

• 出现最差情况的概率很低： 虽然快速排序的最差时间复杂度为 ，不如归并排序，但绝大部分情况下，快速排序可以达到  的复杂度。
• 缓存使用效率高： 哨兵划分操作时，将整个子数组加载入缓存中，访问元素效率很高。而诸如「堆排序」需要跳跃式访问元素，因此不具有此特性。
• 复杂度的常数系数低： 在提及的三种算法中，快速排序的 比较、赋值、交换 三种操作的总体数量最少（类似于插入排序快于冒泡排序的原因）。

算法优化

基准数优化

普通快速排序在某些输入下的时间效率变差。

举个极端例子，假设输入数组是完全倒序的，由于我们选取最左端元素为基准数，那么在哨兵划分完成后，基准数被交换至数组最右端，从而 左子数组长度为 n−1 、右子数组长度为 0 。这样进一步递归下去，每轮哨兵划分后的右子数组长度都为 0 ，分治策略失效，快速排序退化为冒泡排序了。

为了尽量避免这种情况发生，我们可以优化一下基准数的选取策略。首先，在哨兵划分中，我们可以随机选取一个元素作为基准数。但如果运气很差，每次都选择到比较差的基准数，那么效率依然不好。

进一步地，我们可以在数组中选取 3 个候选元素（一般为数组的首、尾、中点元素），并将三个候选元素的中位数作为基准数，这样基准数“既不大也不小”的概率就大大提升了。当然，如果数组很长的话，我们也可以选取更多候选元素，来进一步提升算法的稳健性。采取该方法后，时间复杂度劣化至  的概率极低。

python

""" 选取三个元素的中位数 """
def median_three(self, nums, left, mid, right):# 使用了异或操作来简化代码# 异或规则为 0 ^ 0 = 1 ^ 1 = 0, 0 ^ 1 = 1 ^ 0 = 1if (nums[left] > nums[mid]) ^ (nums[left] > nums[right]):return leftelif (nums[mid] < nums[left]) ^ (nums[mid] > nums[right]):return midreturn right""" 哨兵划分（三数取中值） """
def partition(self, nums, left, right):# 以 nums[left] 作为基准数med = self.median_three(nums, left, (left + right) // 2, right)# 将中位数交换至数组最左端nums[left], nums[med] = nums[med], nums[left]# 以 nums[left] 作为基准数# 下同省略...

C++

/* 选取三个元素的中位数 */
int medianThree(vector& nums, int left, int mid, int right) {// 使用了异或操作来简化代码// 异或规则为 0 ^ 0 = 1 ^ 1 = 0, 0 ^ 1 = 1 ^ 0 = 1if ((nums[left] > nums[mid]) ^ (nums[left] > nums[right]))return left;else if ((nums[mid] < nums[left]) ^ (nums[mid] < nums[right]))return mid;elsereturn right;
}/* 哨兵划分（三数取中值） */
int partition(vector& nums, int left, int right) {// 选取三个候选元素的中位数int med = medianThree(nums, left, (left + right) / 2, right);// 将中位数交换至数组最左端swap(nums, left, med);// 以 nums[left] 作为基准数// 下同省略...
}

尾递归优化

普通快速排序在某些输入下的空间效率变差。

仍然以完全倒序的输入数组为例，由于每轮哨兵划分后右子数组长度为 0 ，那么将形成一个高度为 n−1 的递归树，此时使用的栈帧空间大小劣化至 O(n) 。

为了避免栈帧空间的累积，我们可以在每轮哨兵排序完成后，判断两个子数组的长度大小，仅递归排序较短的子数组。由于较短的子数组长度不会超过 n/2 ，因此这样做能保证递归深度不超过 log⁡n ，即最差空间复杂度被优化至 O(log⁡n) 。

python

""" 快速排序（尾递归优化） """
def quick_sort(self, nums, left, right):# 子数组长度为 1 时终止while left < right:# 哨兵划分操作pivot = self.partition(nums, left, right)# 对两个子数组中较短的那个执行快排if pivot - left < right - pivot:self.quick_sort(nums, left, pivot - 1)  # 递归排序左子数组left = pivot + 1     # 剩余待排序区间为 [pivot + 1, right]else:self.quick_sort(nums, pivot + 1, right)  # 递归排序右子数组right = pivot - 1    # 剩余待排序区间为 [left, pivot - 1]

C++

/* 快速排序（尾递归优化） */
void quickSort(vector& nums, int left, int right) {// 子数组长度为 1 时终止while (left < right) {// 哨兵划分操作int pivot = partition(nums, left, right);// 对两个子数组中较短的那个执行快排if (pivot - left < right - pivot) {quickSort(nums, left, pivot - 1);  // 递归排序左子数组left = pivot + 1;  // 剩余待排序区间为 [pivot + 1, right]} else {quickSort(nums, pivot + 1, right); // 递归排序右子数组right = pivot - 1; // 剩余待排序区间为 [left, pivot - 1]}}
}