[Leetcode] 二叉树的遍历
转载自(有删减和少量改动) 图解二叉树的四种遍历 https://leetcode.cn/problems/binary-tree-preorder-traversal/solution/tu-jie-er-cha-shu-de-si-chong-bian-li-by-z1m/
1. 相关题目
144.二叉树的前序遍历 https://leetcode.cn/problems/binary-tree-preorder-traversal/
94. 二叉树的中序遍历 https://leetcode.cn/problems/binary-tree-inorder-traversal
145. 二叉树的后序遍历 https://leetcode.cn/problems/binary-tree-postorder-traversal/submissions/
102. 二叉树的层序遍历 https://leetcode.cn/problems/binary-tree-level-order-traversal/
2. 基本概念
二叉树
首先,二叉树是一个包含节点,以及它的左右孩子的一种数据结构。
遍历方式
如果对每一个节点进行编号,你会用什么方式去遍历每个节点呢?
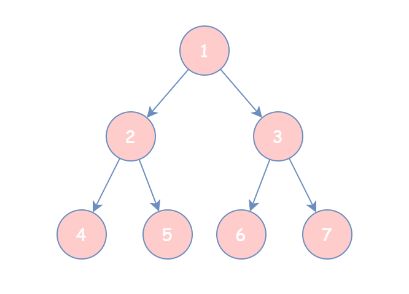
按照 根节点 -> 左孩子 -> 右孩子 的方式遍历,即「先序遍历」,遍历结果为 1 2 4 5 3 6 7;
按照 左孩子 -> 根节点 -> 右孩子 的方式遍历,即「中序遍历」,遍历结果为 4 2 5 1 6 3 7;
按照 左孩子 -> 右孩子 -> 根节点 的方式遍历,即「后序遍历」,遍历结果为 4 5 2 6 7 3 1;
最后,层次遍历就是按照每一层从左向右的方式进行遍历,遍历结果为 1 2 3 4 5 6 7。
3. 题目解析
这四道题目描述是相似的,给定一个二叉树,让我们使用一个数组来返回遍历结果,首先来看递归解法。
3.1 递归解法
在此只介绍前三种的递归解法。它们的模板相对比较固定,一般都会新增一个 dfs 函数:
def dfs(root):if not root:returnres.append(root.val)dfs(root.left)dfs(root.right)对于前序、中序和后序遍历,只需将递归函数里的 res.append(root.val) 放在不同位置即可,然后调用这个递归函数。
3.1.1 前序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res = []def dfs(root):if not root:returndfs(root.left)res.append(root.val)dfs(root.right)dfs(root)return res3.1.2 中序遍历
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res = []def dfs(root):if not root:returndfs(root.left)res.append(root.val)dfs(root.right)dfs(root)return res3.1.3 后序遍历
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res = []def dfs(root):if not root:returndfs(root.left)dfs(root.right)res.append(root.val)dfs(root)return res3.2 迭代解法
3.2.1 前序遍历
3.2.1.1 层层入栈
我们使用栈来进行迭代,过程如下:
初始化栈,并将根节点入栈;
当栈不为空时:
弹出栈顶元素 node,并将值添加到结果中;
如果 node 的右子树非空,将右子树入栈;
如果 node 的左子树非空,将左子树入栈;
由于栈是“先进后出”,所以先将右子树入栈,这样使得前序遍历结果为 “根->左->右”的顺序。
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:stack, res = [root], []while stack:node = stack.pop()if node:#根节点的值加入到结果中res.append(node.val) #右子树入栈if node.right:stack.append(node.right)#左子树入栈if node.left:stack.append(node.left) return res 3.2.1.3 层层入栈(使用标志位)
输出的顺序“根 -> 左 -> 右”,入栈的顺序“右 -> 左 -> 根”。
入栈时额外加入一个标识 flag = 0。每次从栈中弹出元素时,如果 flag 为 0,则需要将 flag 变为 1 并连同该节点再次入栈,只有当 flag 为 1 时才可将该节点加入到结果中。
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack, res = [(0,root)], []while stack:flag, node = stack.pop()#if not node: continueif node:#遍历过了,加入结果if flag == 1:res.append(node.val)else:stack.append((0,node.right)) #右stack.append((0,node.left)) #左stack.append((1,node)) #根return res3.2.1.2 根节点和左孩子先入栈
模板解法的思路稍有不同,它先将根节点 cur 和所有的左孩子入栈并加入结果中,直至 cur 为空,用一个 while 循环实现。
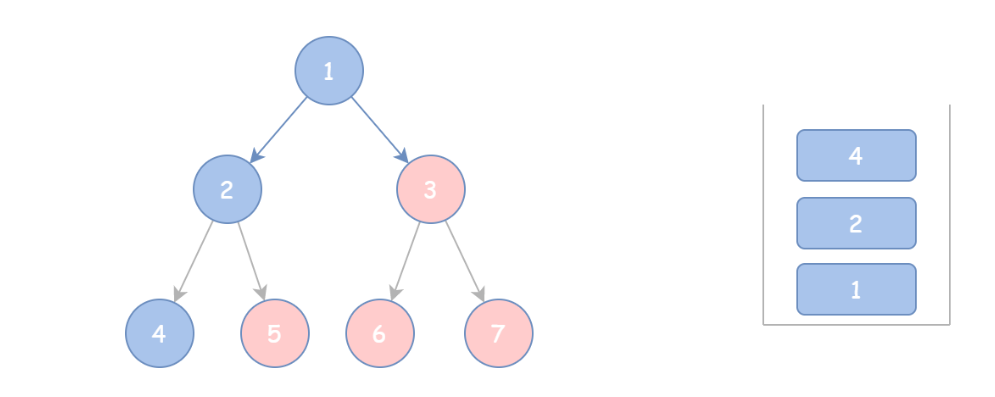
然后,每弹出一个栈顶元素 tmp,就到达它的右孩子,再将这个节点当作 cur 重新按上面的步骤来一遍,直至栈为空。这里又需要一个 while 循环。
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []cur, stack, res = root, [], []while cur or stack:while cur:#根节点和左孩子入栈res.append(cur.val)stack.append(cur)cur = cur.left#每弹出一个元素就达到右孩子tmp = stack.pop()cur = tmp.rightreturn res 3.2.2 中序遍历
3.2.2.1 层层入栈(使用标志位)
和前序遍历的代码类似,区别只是入栈顺序。
输出的顺序“左 -> 根 -> 右”,入栈的顺序“右 -> 根 -> 左”。
入栈时额外加入一个标识 flag = 0,每次从栈中弹出元素时,如果 flag 为 0,则需要将 flag 变为 1 并连同该节点再次入栈,只有当 flag 为 1 时才可将该节点加入到结果中。
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack, res = [(0,root)], []while stack:flag, node = stack.pop()#if not node: continueif node:#遍历过了,加入结果if flag == 1:res.append(node.val)else:stack.append((0,node.right)) #右stack.append((1,node)) #根stack.append((0,node.left)) #左return res3.2.2.2 根节点和左孩子先入栈
和前序遍历的代码类似,只是在出栈的时候才将节点 tmp 的值加入到结果中。
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []cur, stack, res = root, [], []while cur or stack:while cur:#根节点和左孩子入栈,到达最左端的叶子节点stack.append(cur)cur = cur.lefttmp = stack.pop()#出栈时再加入结果res.append(tmp.val)cur = tmp.right 3.2.3 后序遍历
3.2.3.1 层层入栈(使用标志位)
和前序遍历的代码类似,区别只是入栈顺序。
输出的顺序“左 -> 右 -> 根”,入栈的顺序“根 -> 右 -> 左”。
入栈时额外加入一个标识 flag = 0,每次从栈中弹出元素时,如果 flag 为 0,则需要将 flag 变为 1 并连同该节点再次入栈,只有当 flag 为 1 时才可将该节点加入到结果中。
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack, res = [(0,root)], []while stack:flag, node = stack.pop()#if not node: continueif node:#遍历过了,加入结果if flag == 1:res.append(node.val)else:stack.append((1,node)) #根stack.append((0,node.right)) #右stack.append((0,node.left)) #左return res3.2.3.2 根节点和左孩子先入栈
节点 cur 先到达最右端的叶子节点并将路径上的节点入栈;
然后每次从栈中弹出一个元素后,cur 到达它的左孩子,并将左孩子看作 cur 继续执行上面的步骤。
最后将结果反向输出即可。
说明:
1.参考前序遍历的实现,可以达到输出 “根 -> 右 -> 左 ”,逆序即为预期输出。
2.后序遍历采用模板解法并没有按照真实的栈操作,而是利用了结果的特点反向输出。
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []cur, stack, res = root, [], []while cur or stack:while cur:#先到达最右端res.append(cur.val)stack.append(cur)cur = cur.righttmp = stack.pop()cur = tmp.leftreturn res[::-1]3.3 层序遍历
二叉树的层序遍历的迭代方法与前面不用,前面的都采用了深度优先搜索的方式,而层次遍历使用了广度优先搜索,广度优先搜索主要使用队列实现。
广度优先搜索的步骤为:
初始化队列 q,并将根节点 root 加入到队列中;
当队列不为空时:
队列中弹出节点 node,加入到结果中;
如果左子树非空,左子树加入队列;
如果右子树非空,右子树加入队列;
题目描述:
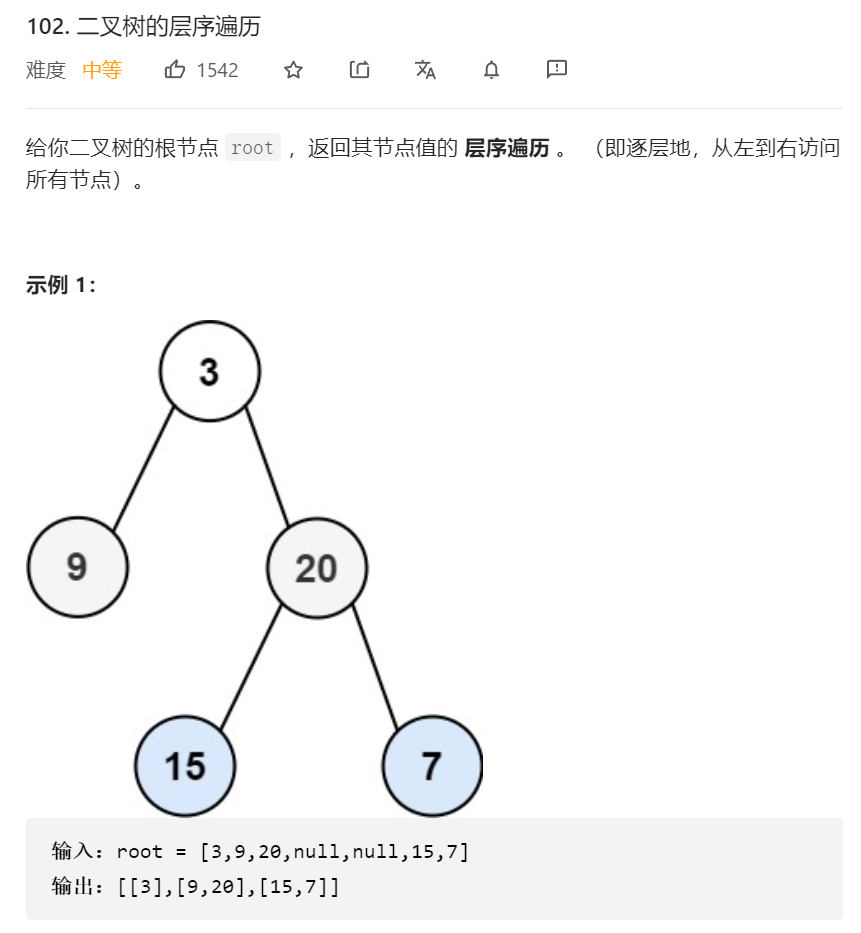
由于题目要求每一层保存在一个子数组中,所以用 level 保存每层的遍历结果,并使用 for 循环来实现。
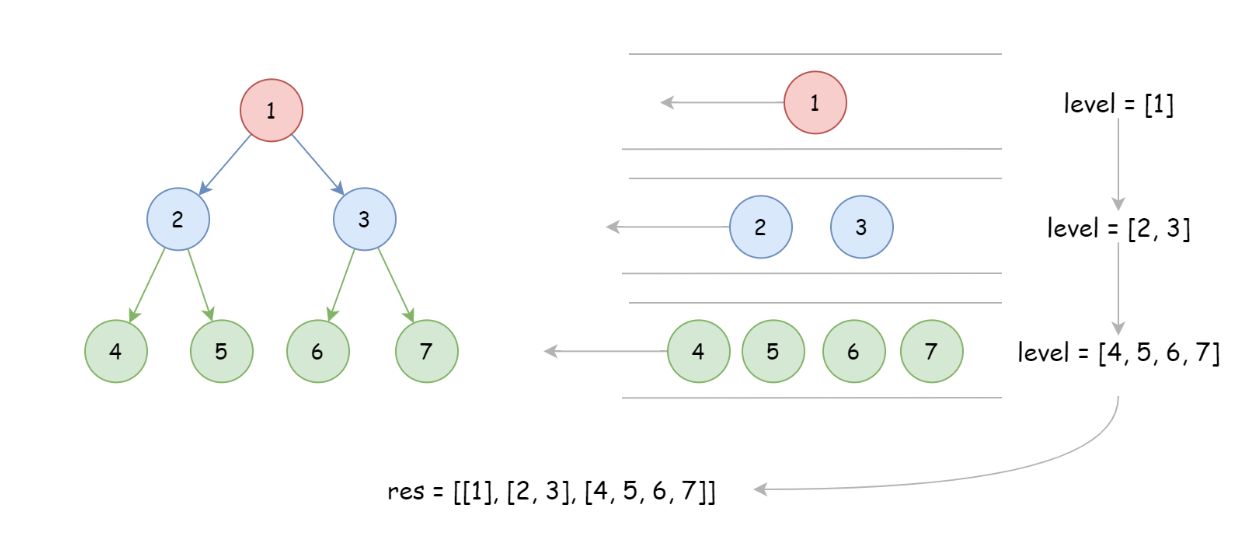
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []res, q = [], [root]while q:n = len(q)level = []for i in range(n):#从队列中逐个弹出该层的每个节点node = q.pop(0)level.append(node.val)#将节点的左右孩子加到队尾,供下一层遍历使用q.append(node.left) if node.left else 1q.append(node.right) if node.right else 1res.append(level)return res