论文笔记Neural Ordinary Differential Equations
论文笔记Neural Ordinary Differential Equations
- 概述
- 参数的优化
- 连续标准化流(Continuous Normalizing Flows)
- 生成式的隐轨迹时序模型(A generative latent function time-series model)
这篇文章有多个版本,在最初的版本中存在一些错误,建议下载2019年的最新版。
概述
在残差网络中有下面的形式:
ht+1=ht+f(ht,θt)(1)\mathbf h_{t+1} = \mathbf h_{t} + f(\mathbf h_{t}, \theta_t) \tag{1} ht+1=ht+f(ht,θt)(1)
连续的动态系统通常可以用常微分方程(ordinary differential equation, ODE)表示为:
dh(t)dt=f(h(t),t,θ)(2)\frac{d\mathbf h(t)}{dt} = f(\mathbf h(t), t, \theta) \tag{2} dtdh(t)=f(h(t),t,θ)(2)如果动态系统中的fff用神经网络的模块表示,就得到了神经常微分方程Neural ODE,公式(1)可以看做是公式(2)的欧拉离散化(Euler discretization)。
输入是h(0)\mathbf h(0)h(0),输出是h(T)\mathbf h(T)h(T),也就是常微分方程初值问题在T时刻的解。
值得注意的是这里的ttt不代表时间,而是代表网络的层数。但在某些问题下,如时间预测问题下,ttt也可以代表时间。
下图所示是残差网络和神经常微分方程的区别。纵轴代表ttt(depth),残差网络的状态变化是离散的,在整数位置计算状态的值,而神经常微分方程的状态是连续变化的,计算状态值的位置由求解常微分方程的算法决定。
实际上Neural ODE中的depth的定义并不简单,这在论文第3部分有说,并不是t为多少就是多深,Neural ODE中的depth应该是和隐含状态计算的次数相关的。比如下图中depth到5,resnet确实只计算了5次隐含状态,但Neural ODE其实计算了很多次的隐含状态。隐含状态计算的次数和终点t有关,和ODE的求解算法也有关。
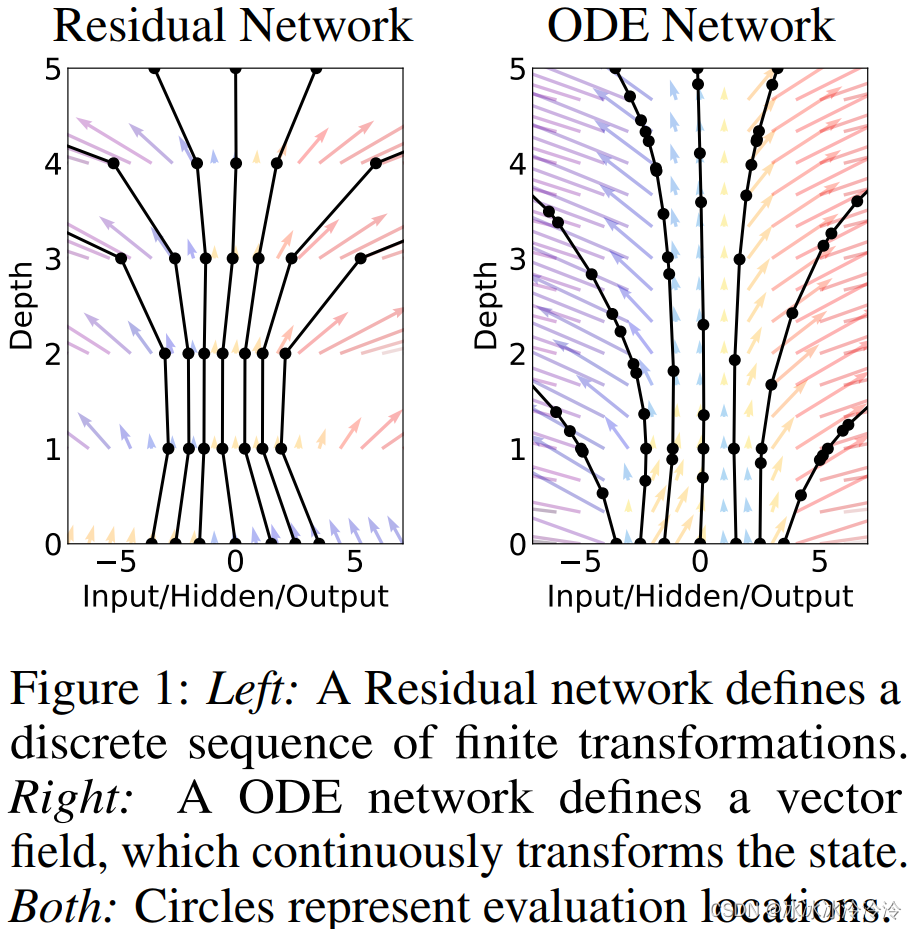
Neural ODE就是用神经网络模块来表示常微分方程里的fff,同时Neural ODE又可以把常微分方程作为一个模块嵌入大的神经网络中。
参数的优化
普通的常微分方程中的参数θ\thetaθ是固定的,但是在Neural ODE中是神经网络的参数,所以需要优化。神经网络的参数用反向传播进行优化,神经常微分方程作为神经网络的一个模块,也需要支持反向传播。因为不只需要优化神经常微分方程中的参数,要需要优化神经常微分方程之前的模块的参数,所以需要求损失函数关于z(t0),t0,t1,θ\mathbf z(t_0), t_0, t_1, \thetaz(t0),t0,t1,θ的梯度。
直接对积分的前向过程做反向传播理论上是可行的,但是需要大量的内存并会导致额外的数值误差。
为了解决这些问题,论文提出使用adjoint sensitivity method来求梯度。adjoint法可以通过求解另一个ODE来计算反传时需要的梯度。
考虑优化一个标量损失函数,这个损失函数的输入是ODE的结果。
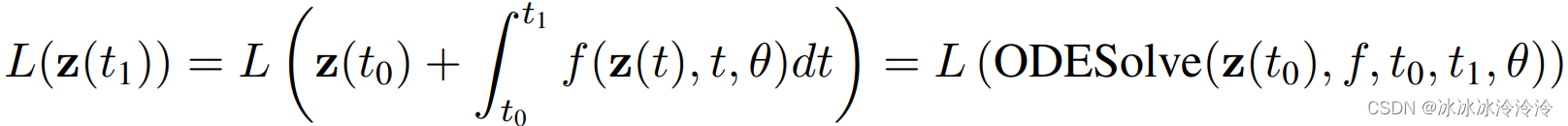
定义伴随状态(adjoint state)为a(t)=−∂L∂z(t)\mathbf a(t)=-\frac{\partial L}{\partial \mathbf z(t)}a(t)=−∂z(t)∂L。
adjoint state满足另一个ODE:
da(t)dt=−a(t)⊤∂f(z(t),t,θ)∂z\frac{d \mathbf a(t)}{dt} = -\mathbf a(t)^\top \frac{\partial f(\mathbf z(t), t, \theta)}{\partial \mathbf z} dtda(t)=−a(t)⊤∂z∂f(z(t),t,θ)论文在附录中给出了证明。
通过伴随状态,损失函数关于z(t0),t0,t1,θ\mathbf z(t_0), t_0, t_1, \thetaz(t0),t0,t1,θ的梯度都可以通过求解ODE得到。
∂L∂z(t0)=a(t1)−∫t1t0a(t)⊤∂f(t,z(t),θ)∂z(t)dt\frac{\partial L}{\partial \mathbf z(t_0)} = \mathbf a(t_1) - \int_{t_1}^{t_0} \mathbf a(t)^{\top}\frac{\partial f(t,\mathbf z(t), \theta)}{\partial \mathbf z(t)} dt ∂z(t0)∂L=a(t1)−∫t1t0a(t)⊤∂z(t)∂f(t,z(t),θ)dt其中a(t1)\mathbf a(t_1)a(t1)是损失函数对最后时刻的隐藏状态的梯度,可以由下一层神经网络的BP获得。
令aθ(t)=∂L∂θ(t),at(t)=∂L∂t(t)\mathbf a_\theta(t) = \frac{\partial L}{\partial\theta(t)}, \ a_t(t) = \frac{\partial L}{\partial t(t)}aθ(t)=∂θ(t)∂L, at(t)=∂t(t)∂L,
∂L∂θ(t0)=aθ(t1)−∫t1t0a(t)⊤∂f(t,z(t),θ)∂θdt\frac{\partial L}{\partial\theta(t_0)} = \mathbf a_\theta(t_1) - \int_{t_1}^{t_0} \mathbf a(t)^{\top}\frac{\partial f(t, \mathbf z(t), \theta)}{\partial\theta} dt ∂θ(t0)∂L=aθ(t1)−∫t1t0a(t)⊤∂θ∂f(t,z(t),θ)dt其中令aθ(t1)=0\mathbf a_\theta(t_1)=0aθ(t1)=0,这一点我目前没有看懂为啥这么设置,θ\thetaθ是不随着ttt而变的。
∂L∂t1=∂L∂z(t1)∂z(t1)∂t1=a(t1)⊤f(t1,z(t1),θ)=at(t1)\frac{\partial L}{\partial t_1} = \frac{\partial L}{\partial \mathbf z(t_1)} \frac{\partial \mathbf z(t_1)}{\partial t_1} = \mathbf a(t_1)^{\top} f(t_1, \mathbf z(t_1), \theta) = a_t(t_1) ∂t1∂L=∂z(t1)∂L∂t1∂z(t1)=a(t1)⊤f(t1,z(t1),θ)=at(t1)∂L∂t0=at(t1)−∫t1t0a(t)⊤∂f(t,z(t),θ)∂tdt\frac{\partial L}{\partial t_0} = a_t(t_1) - \int_{t_1}^{t_0} \mathbf a(t)^{\top}\frac{\partial f(t, \mathbf z(t), \theta)}{\partial t} dt ∂t0∂L=at(t1)−∫t1t0a(t)⊤∂t∂f(t,z(t),θ)dt
这些导数可以整合放到一个ODE方程中去求解,如下面的算法所示:

实际使用中不需要考虑梯度计算的问题,因为这些在库(https://github.com/rtqichen/torchdiffeq)中都已经写好了,只需要定义好fff直接调用积分算法就可以了。
连续标准化流(Continuous Normalizing Flows)
公式(1)中这种形式也出现在标准化流中(normalizing flows)。
normalizing flows是一种生成算法,可以学习模型生成指定分布的数据,目前广泛用于图像的生成。
normalizing flows要求变换是双射(bijective fucntion),这样就可以利用change of variables theorem直接计算概率。
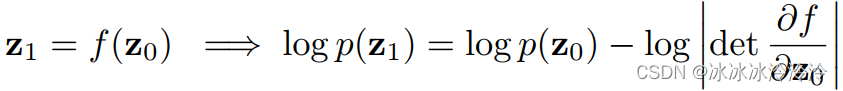
为了满足双射的要求,变换需要是精心设计的。normalizing flows有不同的变种方法,其中一种planar normalizing flow有下面的变换:
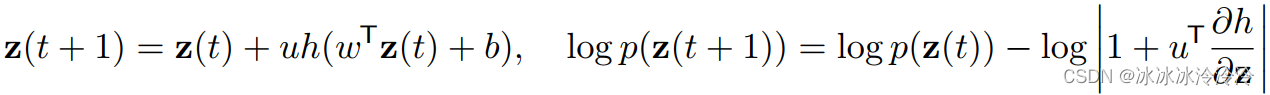
主要的运算量来着于计算∂f∂z\frac{\partial f}{\partial \mathbf z}∂z∂f。有趣的是当离散的变换变为连续的变换时,概率的计算变得简单了,不再需要det的计算。
论文给出了下面的定理:

值得注意的是,后面火起来的生成模型diffusion model,可以扩展为probability flow ODE,也可以使用这个定理。
生成式的隐轨迹时序模型(A generative latent function time-series model)
在时序模型中ttt可以表示时间。用Neural ODE建模时间序列的好处是可以建模连续的状态,天然适合非规则采样的时间序列(irregularly-sampled data)。
假设每一个时间序列由一个隐轨迹决定。隐轨迹是由初始状态和一组隐含的动态决定的。有观测时间点t0,t1,⋯,tNt_0,t_1,\cdots,t_Nt0,t1,⋯,tN和初始状态zt0z_{t_0}zt0,生成模型如下:
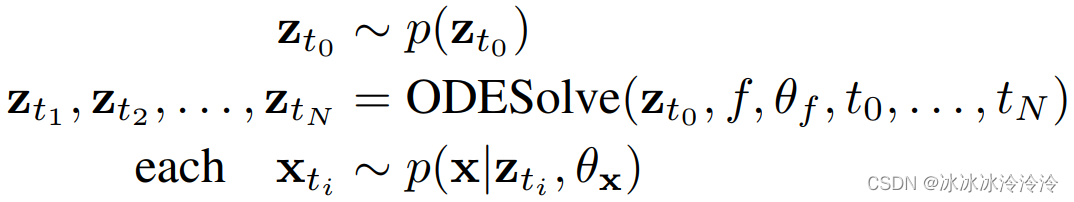
这里fff被定义为一个不随着时间变换的神经网络。外推(Extrapolating)可以得到时间点往前或者往后的预测结果。
这本质是一个隐变量生成模型,所以可以用variational autoencoder(VAE)的算法优化。只不过这里的观测变量时间序列,而传统VAE的观测变量是图像。
为了能表示时间序列,这里encoder使用的是RNN模型。生成初始隐含状态后,由Neural ODE生成其他时间点的隐含状态,再由一个decoder网络计算p(x∣z)p(x|z)p(x∣z)。
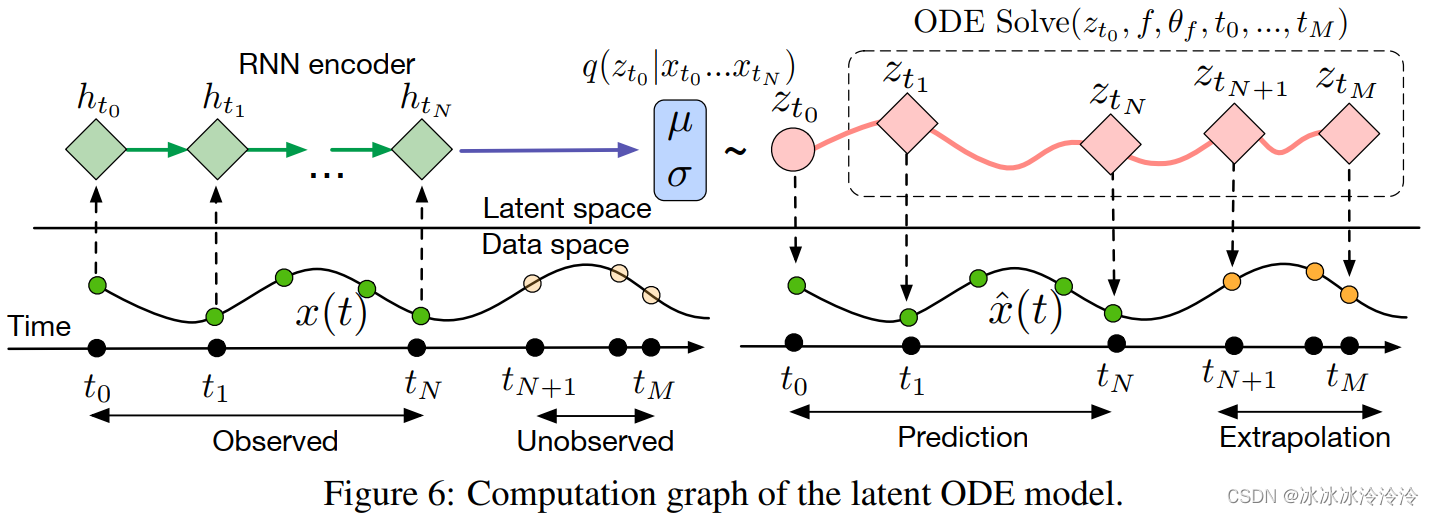
上一篇:天津人才引进迁出迁入延期经验分享
下一篇:线段树讲解
