Description

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

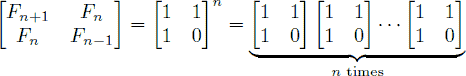
Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

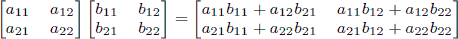
Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

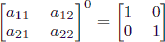
知识点矩阵快速幂加速递推

#include 
#include 
#include 
#include 
#include 
#include using namespace std;
typedef long long ll;const ll m = 10000;
// 矩阵的快速幂
struct matrix{ ll m[3][3]; };
matrix operator *(const matrix& a, const matrix& b) { // 重载*为矩阵乘法，注意constmatrix c;memset(c.m,0, sizeof(c.m));for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {for (int k = 0; k < 2; k++) {c.m[i][j] = (c.m[i][j] + a.m[i][k] * b.m[k][j]) % m;}}}return c;
}matrix pow_matrix(matrix a, ll n) {matrix ans;memset(ans.m, 0, sizeof(ans.m));for (int i = 0; i < 2; i++) ans.m[i][i] = 1;while (n) {if (n & 1) ans = ans * a;a = a * a;n >>= 1;}return ans;
}
int main() {ll n;while (cin >> n ,n != EOF){if (n == -1)break;if (n == 0){printf("0\n");continue;}matrix a;a.m[0][0] = 1; a.m[0][1] = 1;a.m[1][0] = 1; a.m[1][1] = 0;a = pow_matrix(a, n);printf("%lld\n", a.m[0][1]);}return 0;
}