树状数组代码模板

普通数组：求前缀和： O(n)O(n)O(n)，修改：O(1)O(1)O(1)

前缀和数组：求前缀和：O(1)O(1)O(1)，修改：O(n)O(n)O(n)

鱼和熊掌不可兼得，当我们同时需要对一个数组求前缀和和修改时，这两种数组的时间复杂度都比较高。

而树状数组是一个折中的方案，它运用二进制优化，求前缀和和修改操作的时间复杂度都是 O(log⁡n)O(\log n)O(logn)

下面是代码模板：

• tr 树状数组，下标从 1 开始
• add 在下标为 x 的位置加 c
• sum 求下标 [1,x][1,x][1,x] 的元素的和

const int N = 100010;int n;
int tr[N];int lowbit(int x) {return x & -x;
}void add(int x, int c) {for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}int sum(int x) {int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}

因为代码比较简短，所以你可以直接把它背下来，使用的时候 tr 数组就当成普通的数组看待，但是只能通过 add 和 sum 函数对它进行操作

原理

lowbit 函数

lowbit 函数用来求一个数的二进制表示的最低一位 111 所表示的数。如 lowbit(6)=2lowbit(6) = 2lowbit(6)=2，666 的二进制为 110110110，最低一位 111 就是 101010 即为 222。

技巧是
x&−x\rm x\ \&\ -x x & −x
负数在计算机中存储的是补码，补码就是一个数的二进制按位取反然后加 111，−x-x−x 在计算机中的存储就是将 xxx 取反再加 111

因此获取 xxx 最低一位 111 的原理如下：

• 假设 xxx 的二进制表示为 (a10⋯0)2(a10\cdots0)_2(a10⋯0)2​，其中 aaa 表示若干个高位，111 表示最低位的那个 111，0⋯00\cdots00⋯0 表示后面的若干个 000，那么 −x-x−x 的二进制表示为

• (a‾01⋯1)2+(1)2=(a‾10⋯0)2(\overline{a}01\cdots1)_2+(1)_2=(\overline{a}10\cdots0)_2 (a01⋯1)2​+(1)2​=(a10⋯0)2​

  其中 a‾\overline{a}a 表示高位的 aaa 按位取反。

• 最后 (a‾10⋯0)2&(a10⋯0)2=(10⋯0)2(\overline{a}10\cdots0)_2\ \&\ (a10\cdots0)_2 = (10\cdots0)_2(a10⋯0)2​ & (a10⋯0)2​=(10⋯0)2​，即求出了最低一位 111

树状数组则是这样一种思路：

如果我们要求前 (11010)2(11010)_2(11010)2​ 项的和，可以先求前 (10000)2(10000)_2(10000)2​ 项的和，再求接下来 (1000)2(1000)_2(1000)2​ 项的和，最后求接下来 (10)2(10)_2(10)2​ 项的和，然后把这三个和相加，就是我们要求的答案了。因为只要枚举每一位 111，所以时间复杂度为 O(log⁡n)O(\log n)O(logn)

根据这个思路，我们给出两个定义：

• 设原数组为 a[]\rm a[]a[]

• tr[i]\rm tr[i]tr[i] 即为原数组中，以下标 iii 结尾的长度为 lowbit(i)\rm lowbit(i)lowbit(i) 的后缀子数组的和，即下标 [i−lowbit(i)+1,i][i-{\rm lowbit}(i)+1,i][i−lowbit(i)+1,i] 的范围。

这样 tr[(11010)2]\rm tr[(11010)_2]tr[(11010)2​] 就是原数组中以下标 (11010)2(11010)_2(11010)2​ 为结尾的 (10)2(10)_2(10)2​ 个后缀元素的和，接下来让 (11010)2−(10)2=(11000)2(11010)_2-(10)_2=(11000)_2(11010)2​−(10)2​=(11000)2​，tr[(11000)2]\rm tr[(11000)_2]tr[(11000)2​] 就是以下标 (11000)2(11000)_2(11000)2​ 为结尾的 (1000)2(1000)_2(1000)2​ 个后缀元素的和，以此类推，(11000)2−(1000)2=(10000)2(11000)_2-(1000)_2=(10000)_2(11000)2​−(1000)2​=(10000)2​，tr[(10000)2]\rm tr[(10000)_2]tr[(10000)2​] 就是以下标 (10000)2(10000)_2(10000)2​ 为结尾的 (10000)2(10000)_2(10000)2​ 个后缀元素的和。显然这三个和是不重不漏的，相加即为前 (11010)2(11010)_2(11010)2​ 项和。

如图：

可以看到其实是一个树状结构，箭头表示一种包含关系

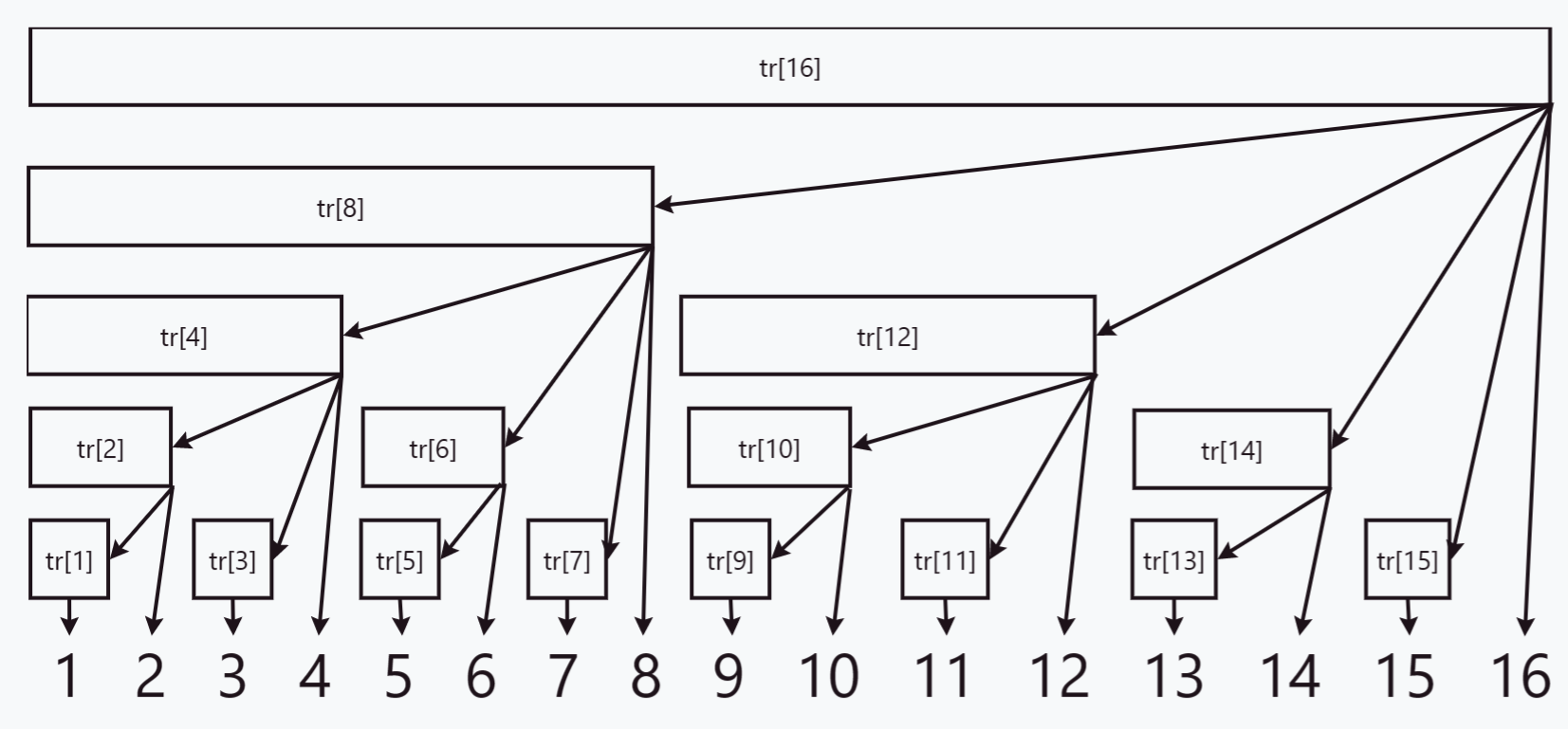
查询前缀和的方法上面已经讲过了，下面我们思考如何进行修改。

要修改原数组 a\rm aa 中某个元素的值，比如修改 a[6]\rm a[6]a[6] ，从图中来看，显然它会影响到 tr[6]、tr[8]、tr[16]\rm tr[6]、tr[8]、tr[16]tr[6]、tr[8]、tr[16] 。也就是要更新从叶子结点 6 到根结点的这条路径。

那么，如何从子结点找父结点？

假设父结点 p=(a10⋯0)2p = (a10\cdots0)_2p=(a10⋯0)2​，那么其子节点为了保证包含于它，也就是，大小比 ppp 小，子数组的长度也比 ppp 短，则子结点 iii 一定是(a01⋯10⋯0)2(a01\cdots10\cdots0)_2(a01⋯10⋯0)2​ 的形式，所以我们只要对子节点 iii 加上一个 lowbit(i)\rm lowbit(i)lowbit(i) 就可以得到父结点。

最后我们提一下树状数组的建树方式：

给定我们一个数组，让我们对其进行建树。

一、

最直接也最常用方式就是使用 add 函数

for (int i = 1; i <= n; ++i) add(i, a[i]);

时间复杂度为 O(nlog⁡n)O(n\log n)O(nlogn)

二、

算每条边

如 tr[12]=tr[10]+tr[11]+a[12]\rm tr[12] = tr[10] + tr[11] + a[12]tr[12]=tr[10]+tr[11]+a[12]

for (int x = 1; x <= n; ++x) {for (int i = x - 1; i >= x - lowbit(x) + 1; i -= lowbit(i)) {tr[x] += tr[i];}
}

时间复杂度为 O(n)O(n)O(n)

三、

直接对原数组求前缀和，然后根据 tr\rm trtr 数组的定义进行建树

for (int i = 1; i <= n; ++i) {a[i] += a[i - 1];tr[i] = a[i] - a[i - lowbit(i)];
}

时间复杂度为 O(n)O(n)O(n)