深度卷积对抗神经网络 基础 第三部分 (WGAN-GP）

Wasserstein GAN with Gradient Penalty (WGAN-GP)

我们在训练对抗神经网络的时候总是出现各种各样的问题。比如说模式奔溃 (mode collapse)和 梯度消失（vanishing gradient）的问题。

比如说，模式奔溃，指的是生成器的学习效率远高于辨别器的时候，那么学习一段时间过后，辨别器便无法再继续提供有用的损失信息，以至于生成器无法得到参考而塌陷到一个局部最小点中去。而梯度消失指的是当损失趋于无限大或者无限小时，损失函数的值变化基本可以视为忽略，那么梯度就会消失，进而停止学习或者学习效率基本为零。

正如GANs模型中，我们经常使用BCE损失函数 （BCE loss problem）来作为模型的损失函数，但是其会存在一定的模式奔溃和梯度消失的问题。 为了解决这个问题，WGAN使用 EMD (Earth mover’s distance) 距离，通过类比定义两个曲线之间距离的方式来定义其损失的函数。

EMD 用于分析两张图片的距离，其实是计算两个分布数据之间的距离，也就是所谓的推土机距离。当其应用于比较生成图像和真图像的距离时，其不会直接想BCEloss那样直接使用判别器的判别结果，而是根据计算生成图像和真图像的分布距离来作为反馈，这样就可以直接避免上述的两个问题。一来模式不会立刻崩溃，而是生成一组图片才会有一个评分结果，并且比较的不是单一图像的差距，而是生成图像和真图像的分布差距。其次，这个距离可以通过对critic函数限制来达到避免梯度消失的问题。

• Function of amount and distance
• Doesn’t have a flat regions when the distributions are very different
• approximating EMD solves mode collapse and vanishing gradient from BCE LOSS

Wasserstein loss: with c(x) critic

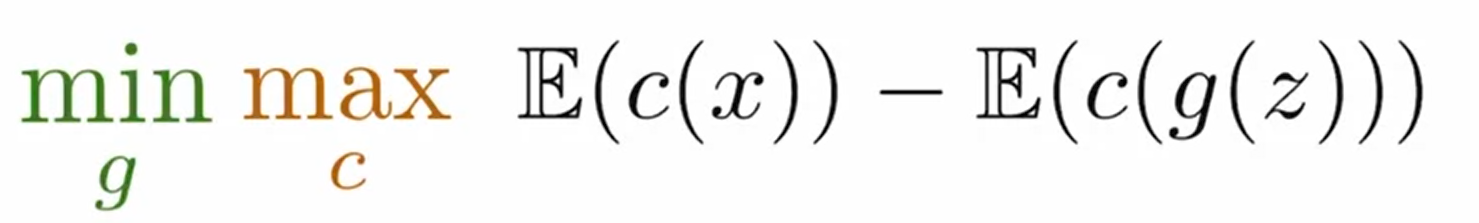
这个函数需要满足 1-Lipschitz 连续条件。This function needs to be 1-Lipschitz Continuous to validate W-loss

其主要是满足训练时的稳定性条件，其斜率的绝对值被正负一所限制。 which will maintain some stability during training

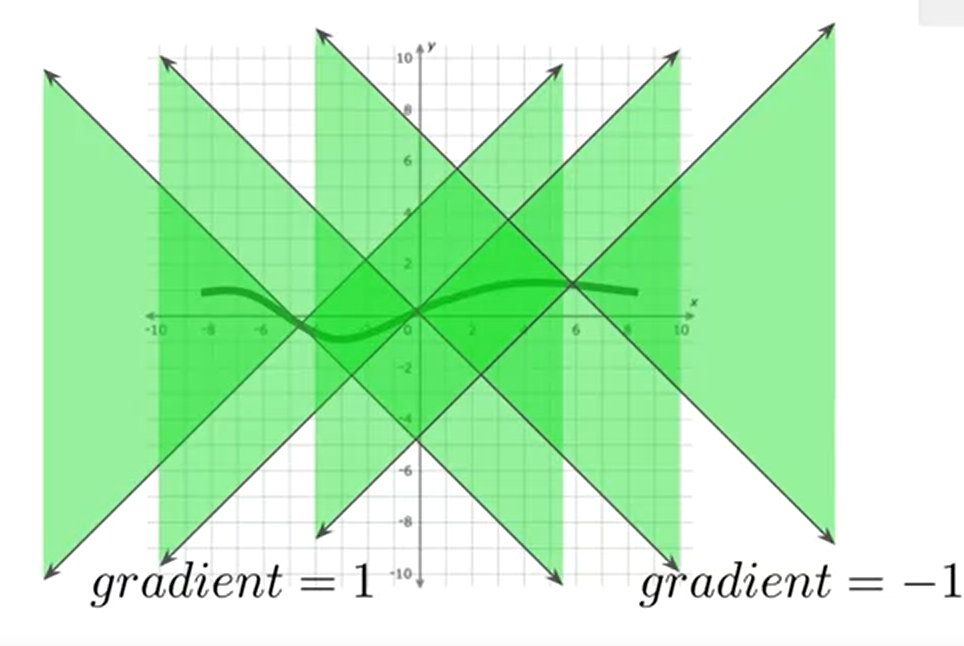
相对于BCE损失函数，W损失函数如何可以变得更加稳定？enforce this condition (feature space)

这个模型通过加入一个修正项的方式来矫正其满足1-lipschitz条件。

那么如何权衡？ How much to weigh this regularization term against the main loss function 如何权衡main loss和penalty使得其满足1-L 连续条件

方法一： 梯度惩罚 Gradient penalty

这个方法很简单，当梯度大于一时，我们通过修正项进行修正，使得学习稳定一些。而如何检测梯度的值也非常重要，如果每次计算损失都检测，那么一定是不值当的。因此我们对特征空间中的点进行插值的方式类进行计算。x^\hat{x}x^便是插值点，我们只要计算插值点的梯度值来代替这一区域的梯度。

• 通过在W-loss中加入一个gradient penalty，当其值大于一时，其gradient过于大，那么我们就控制其小于1.
• 但是又无法对所有feature space中的点都进行插值，因此我们需要将真假照片进行插值处理来计算gradient。
• gradient penalty 用来计算真假的gradient的理想值，我们想要这个值在与正负一的距离**<=1**。

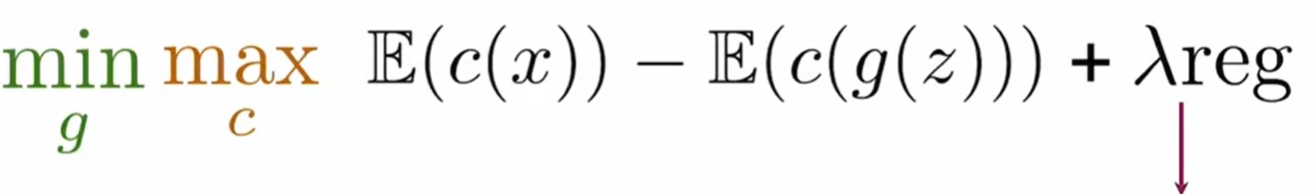
插值interpolation x^\hat{x}x^的表示式为：
x^=ϵx+(1−ϵ)g(z)\hat{x} = \epsilon x + (1- \epsilon)g(z) x^=ϵx+(1−ϵ)g(z)

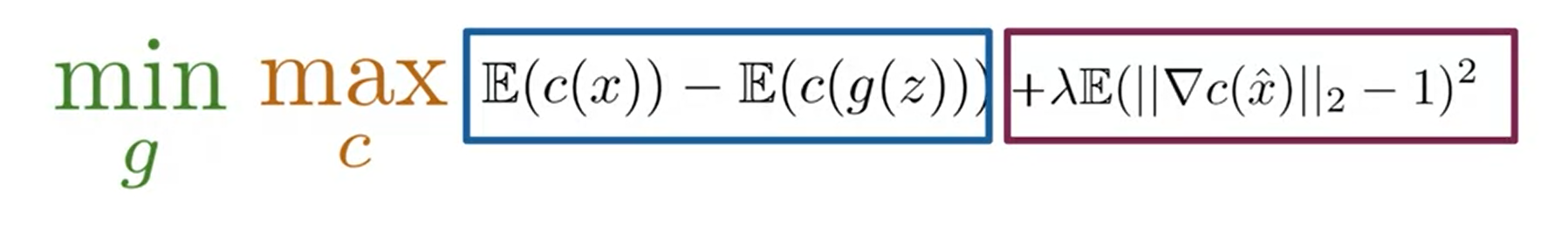
C 表示critisizer, G代表 generator，上述表达式中 第一项 E(c(x))E(c(x))E(c(x)) 指的是C识别真图片的期望，因此，越高越好。第二项 E（c(g(x))）E（c(g(x))）E（c(g(x))）指的是C识别假图片的期望，因此越低越高，这样 第一项减去第二项便是越高越好，因此总体来说，对于C来说，整体项越大越好，C的有效率越高。而在当C取到最有效的鉴别器后，这时，寻找最高效的生成器便是最重要的。那么反过来，第一项无法改变，而第二项则是越大越好，越大意味着C把假图片识别成了真图片，因此整体便是越小越好。这也是为什么会有 min max之说。

• fake 分数越高， critic loss越高，因为fake图片的分数代表着其将假图片识别成1的分数高
• real 分数越高，critic loss越低，因为其识别错误会是0，而识别正确是1，而critic要识别越正确越好，所以越高越好
• gradient penalty越高，critic loss越低，因为其越高，其在中间点的gradient距离1越远，也就意味着其loss越大，因为其gradient和理想1有差别。

方法二： Weight clipping

通过给gradient加入一个上限和下限来使其满足1-L连续条件，问题是这种方法降低了学习能力和速率，不建议采用