AcWing 292. 炮兵阵地（状态压缩DP）

• 一、题目
• 二、思路
• • 1、分析
  • 2、状态表示
  • 3、状态转移
  • 4、循环设计
  • 5、初末状态
• 三、代码

一、题目

二、思路

1、分析

这道题的话和我们之前讲解的AcWing 327. 玉米田（状态压缩DP）和AcWing 1064. 小国王（状态压缩DP）是非常相似的。

此处的做法也是一样的，但是唯一不同的是之前的两道题是利用上一行决定当前行，而今天所讲解的题目是根据前两行来决定当前行。因此，我们需要记录第i行和第i-1行，然后枚举倒数第i-2行。这就是这道题的一个很关键的思路。

然后我们分析一下这道题中合法的情况：
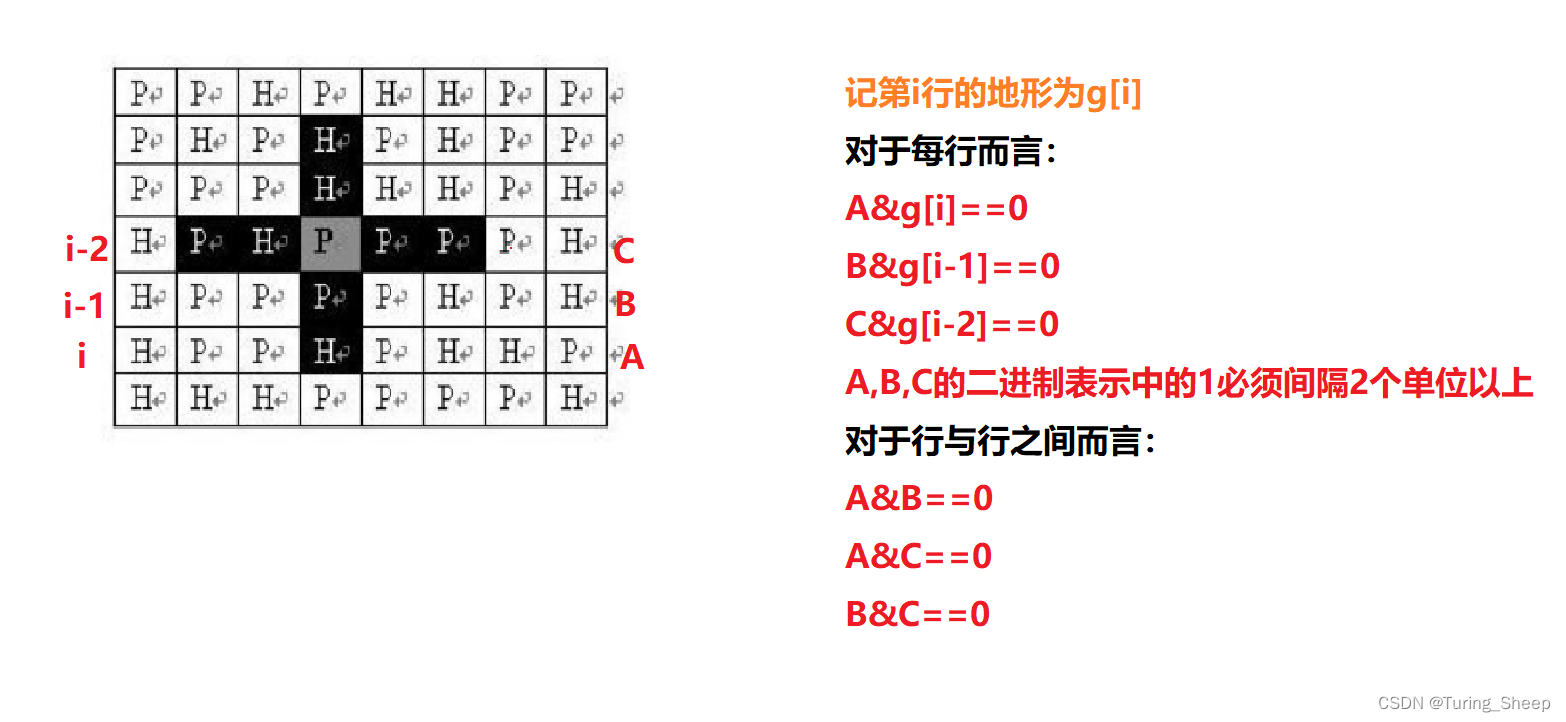这道题和玉米田那道题一样，地图也对我们的结果有一定影响，因此我们需要将地图中每一行的状态也存储下来，我们不妨让p的位置是0，H的位置是1，这样的话，地图中是0的地方才能部署，而我们规定部署部队是1，不部署不对是0，这样就可以产生一个很神奇的效果，如果某个方案状态是合法的，那么这个状态和地图该行的状态做&\&&运算的结果是0。

2、状态表示

f[i][s][ss]f[i][s][ss]f[i][s][ss]表示在前iii行里面部署部队，且第i行的状态是state[s],第i-1行的状态是state[ss]，在这种情况下所能部署的数量的最大值。

由于这道题的行数的最大值是100，所以我们开三维数组的话要注意空间问题，为了减小空间的使用，我们可以使用滚动数组，但是这里为了降低一些理解的难度，我们就使用普通的数组。

我们知道很多状态都是不合法的，所以我们需要预处理出来可能合法的方案，即那些二进制表示中1和1之间都空了两个及两个以上的单位的状态。

当我们将这些预处理出来之后，将其下标作为我们的fff数组的参数。

3、状态转移

f[i][s][ss]=max(f[i−1][ss][si−2]+count(state[s]),f[i][s][ss])f[i][s][ss]=max\big(f[i-1][ss][s_{i-2}]+count(state[s]),f[i][s][ss]\big)f[i][s][ss]=max(f[i−1][ss][si−2​]+count(state[s]),f[i][s][ss])

4、循环设计

循环设计就比较简单了，但是我们涉及到了i-2，为了避免数组越界，我们需要将第0行和第1行空出来，从第2行开始存储。这样可以避免数组越界。

那么外层循环枚举行数，接着枚举第i-2行，然后是第i-1行，最后是第i行。

5、初末状态

最终的结果就是f[n+3][0][0]，这个状态的意思是第n+2行和第n+3行都是空白的。而我们从第2行开始记录，所以我们图的边界就是n+1。恰好n+2和n+3是空白的。

三、代码

#include
#include
#include
#include
using namespace std;
const int N=110,M=10,S=110;
int f[N][S][S];
int g[N];
vectorstate;
int n,m;
bool check(int state)
{for (int i = 0; i < m; i ++ )if ((state >> i & 1) && ((state >> i + 1 & 1) || (state >> i + 2 & 1)))return false;return true;
}int get_nums(int x)
{int res=0;for(int i=0;i>i&1);return res;
}int main()
{cin>>n>>m;for(int i=2;i<=n+1;i++){for(int j=0;jchar c;cin>>c;if(c=='H')g[i]+=1<for(int j=0;jif(state[j]&g[i-2])continue;for(int s=0;sif(state[s]&g[i-1])continue;for(int ss=0;ssif(state[ss]&g[i])continue;if( (state[j] & state[s]) || (state[j] & state[ss] ) || (state[s] & state[ss]) )continue;elsef[i][ss][s]=max(f[i-1][s][j]+get_nums(state[ss]),f[i][ss][s]);}}}}cout<