一、季节分解

1、概念

时间序列也称为动态序列，是指将某种现象的指标数值按照时间顺序排列而成的数值序列。主要由时间要素和数值要素构成。时期序列中，数值要素反映现象在一定时期内发展的结果；时点序列中，数值要素反映现象在一定时点上的瞬间水平。

2、时间序列分解

数值变换的规律性，一般分为以下四种：

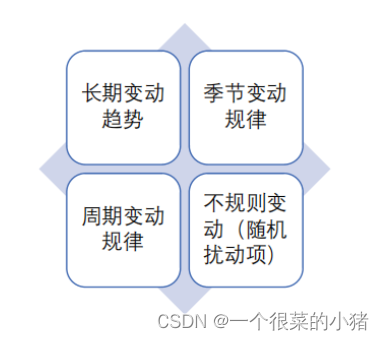
一个时间序列往往是以上四类变化形式的叠加。

• 长期趋势T：持续上升或下降
• 季节趋势S：不以年为单位，如雪糕和棉衣
• 循环变动C：通常以若干年为周期，波浪式的周期变动（非严格规则）
• 不规则变动I：不可预知和没有规律性的，在回归中被称为扰动项

3、叠加模型和乘积模型

四种变动与指标数值最终变动的关系可能是叠加关系，也可能是乘积关系。

4、Spss处理时间序列中的缺失值

• 缺失值在开头或尾部，可直接删除
• 缺失值发生在序列中间，不能删除，可替换（序列平均值、临近点的平均值、临近点的中位数、线性插值、邻近点的线性趋势）

二、指数平滑法模型

1、Simple模型（简单指数平滑法）

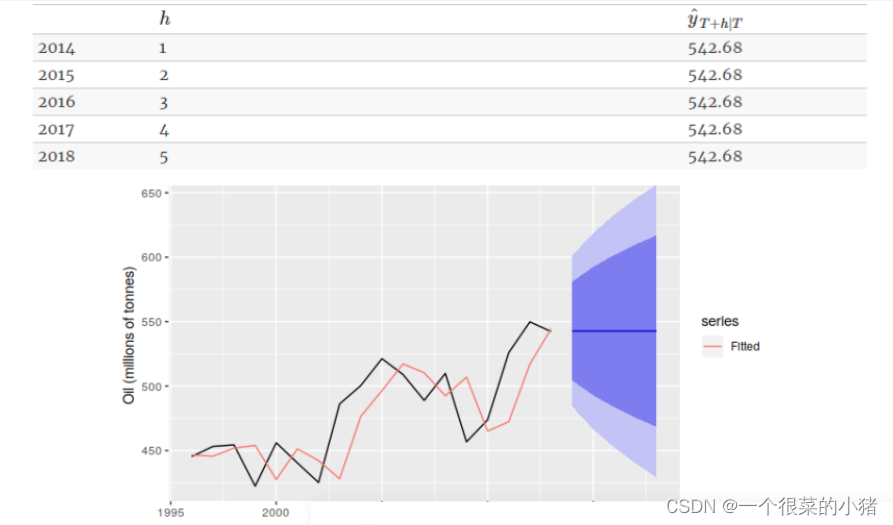
2、线性趋势模型

3、阻尼趋势模型

4、简单季节性

三、自回归模型（Autoregressive model，简称AR）

用x1x_{1}x1​至xt−1x_{t-1}xt−1​来预测本期xtx_{t}xt​的表现，并假设它们为线性关系。因为这是从回归分析中的线性回归发展而来，只是不用x预测y，而是用x预测x（自己），所以叫做自回归。
可用如下差分方程来表示：

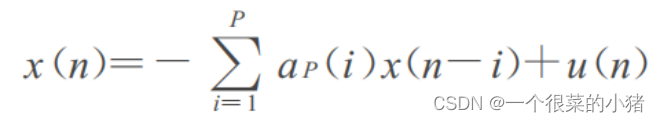
1、油价序列零均值化后的数据

clear;
%--------------------------------油价序列零均值化后的数据如下----------------------------------------%：
P=[ 19.5900   14.9100   15.7400   15.4000   13.0600   19.0700   15.2800   15.8200   12.7700   12.0500...  11.6900   13.8500   13.8500   10.0700    9.1700   10.7900   13.4400   21.1700   18.6400   13.2100...  15.5400   21.9400   23.1100   18.6400   14.9400   16.9000   15.4600   11.1500   13.1300   12.4800...  12.9500   12.5900   10.5800   10.5800   12.3900   15.5300   13.0600   10.2200   16.3300   19.7200...21.3100   18.8400   24.8400   15.6700   15.5700   12.7300   13.5600   15.5400   17.2200   12.1400...11.0700   12.0200   11.5500    6.9200   10.3300   8.3800    12.1100   11.4600   12.7500   13.3200...13.0000   11.9000   11.7900   12.5500   11.8400   11.2500   11.1500   10.9900   11.7000   14.0100...17.5100   17.2700   16.9000   15.7900   15.4500   6.2400    16.7100   16.7700   16.6400   17.8000...16.8700   16.1300   15.7600   15.6600   15.5400   15.3000   15.0500   14.6900   14.3900   14.1800...13.70     13.66     13.27     13.56     13.14     14.19 ];
F=[ 19.5900   14.9100   15.7400   15.4000   13.0600   19.0700   15.2800   15.8200   12.7700   12.0500...  11.6900   13.8500   13.8500   10.0700    9.1700   10.7900   13.4400   21.1700   18.6400   13.2100...15.5400   21.9400   23.1100   18.6400   14.9400   16.9000   15.4600   11.1500   13.1300   12.4800...12.9500   12.5900   10.5800   10.5800   12.3900   15.5300   13.0600   10.2200   16.3300   19.7200...21.3100   18.8400   24.8400   15.6700   15.5700   12.7300   13.5600   15.5400   17.2200   12.1400...11.0700   12.0200   11.5500    6.9200   10.3300   8.3800    12.1100   11.4600   12.7500   13.3200...13.0000   11.9000   11.7900   12.5500   11.8400   11.2500   11.1500   10.9900   11.7000   14.0100...17.5100   17.2700   16.9000   15.7900   15.4500   6.2400    16.7100   16.7700   16.6400   17.8000...16.8700   16.1300   15.7600   15.6600   15.5400   15.3000   15.0500   14.6900   14.3900   14.180];

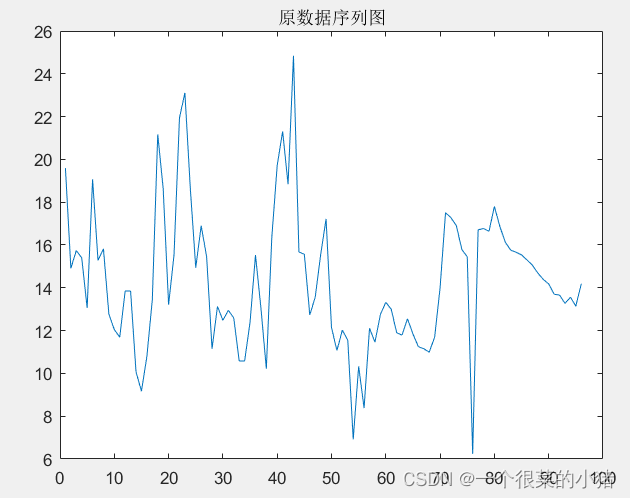
2、消除趋势性

%----------------------由于时间序列有不平稳趋势，进行两次差分运算，消除趋势性----------------------%
for i=2:96Yt(i)=P(i)-P(i-1);
end
for i=3:96L(i)=Yt(i)-Yt(i-1);
end
figure;
L=L(3:96);
Y=L(1:88);
plot(P);
title('原数据序列图');
hold on;
pause 
plot(Y,'r');
title('两次差分后的序列图和原数对比图');
pause  

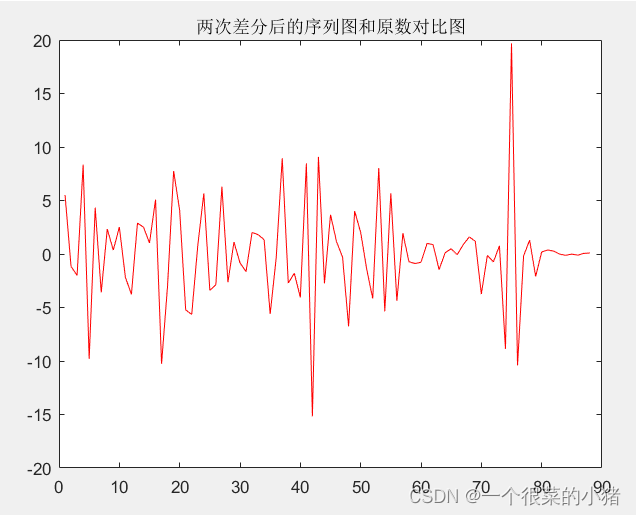
3、对数据标准化处理

%--------------------------------------对数据标准化处理----------------------------------------------%
Ux=sum(Y)/88                           % 求序列均值
yt=Y-Ux;
b=0;
for i=1:88b=yt(i)^2/88+b;
end
v=sqrt(b)                              % 求序列方差
Y=(Y-Ux)/v;                             % 标准化处理公式
f=F(1:88);
t=1:88;
figure;
plot(t,f,t,Y,'r')
title('原始数据和标准化处理后对比图');
xlabel('时间t'),ylabel('油价y');
legend('原始数据 F ','标准化后数据Y ');
pause  

对数据标准化处理

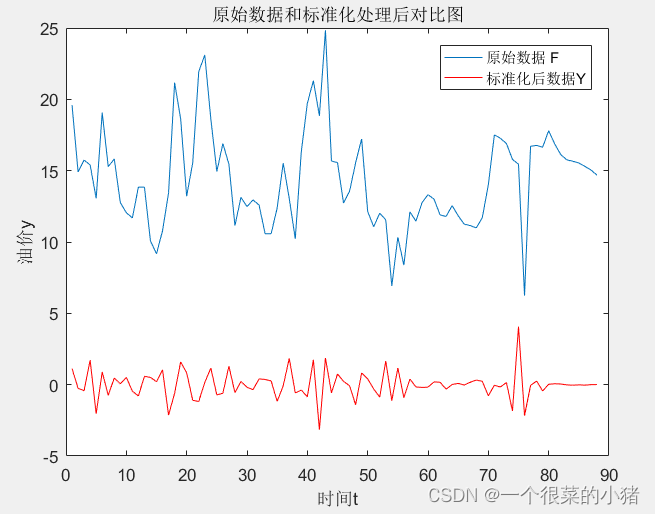
4、计算自相关系数

%------------------------检验预处理后的数据是否符合AR建模要求，计算自相关和偏相关系数---------------%%---------------------------------------计算自相关系数-----------------------------------%
R0=0;
for i=1:88 R0=Y(i)^2/88+R0;
end
R0
for k=1:20R(k)=0;for i=k+1:88R(k)=Y(i)*Y(i-k)/88+R(k);endR                        %自协方差函数R   
end
x=R/R0                      %自相关系数x
figure;
plot(x)
title('自相关系数分析图');
pause  

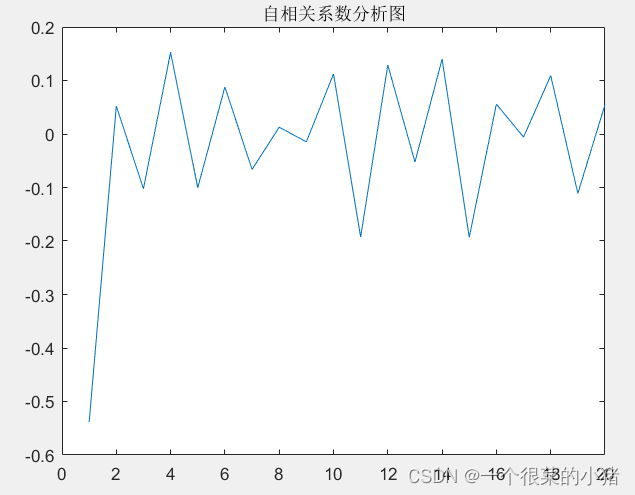
5、计算偏相关函数

   %-----------------------解Y-W方程，其系数矩阵是Toepli矩阵。求得偏相关函数X-----------------------%
X1=x(1);
X11=x(1);
B=[x(1) x(2)]';
x2=[1 x(1)];
A=toeplitz(x2);                      
X2=A\B
X22=X2(2)B=[x(1) x(2) x(3)]';
x3=[1 x(1) x(2)];
A=toeplitz(x3);                      
X3=A\B
X33=X3(3)B=[x(1) x(2) x(3) x(4)]';
x4=[1 x(1) x(2) x(3)];
A=toeplitz(x4);                      
X4=A\B
X44=X4(4)B=[x(1) x(2) x(3) x(4) x(5)]';
x5=[1 x(1) x(2) x(3) x(4)];
A=toeplitz(x5);                      
X5=A\B
X55=X5(5)B=[x(1) x(2) x(3) x(4) x(5) x(6)]';
x6=[1 x(1) x(2) x(3) x(4) x(5)];
A=toeplitz(x6);                      
X6=A\B
X66=X6(6)B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)]';
x7=[1 x(1) x(2) x(3) x(4) x(5) x(6)];
A=toeplitz(x7);                      
X7=A\B
X77=X7(7)B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8)]';
x8=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7)];
A=toeplitz(x8);                      
X8=A\B
X88=X8(8)B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9)]';
x9=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8)];
A=toeplitz(x9);                      
X9=A\B
X99=X9(9)B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10)]';
x10=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9)];
A=toeplitz(x10);                      
X10=A\B   
X1010=X10(10)B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11)]';
x11=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10)];
A=toeplitz(x11);                      
X101=A\B   
X1111=X101(11)B=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11) x(12)]';
x12=[1 x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11)];
A=toeplitz(x12);                      
X12=A\B   
X1212=X12(12)X=[X11 X22 X33 X44 X55 X66 X77 X88 X99 X1010  X1111 X1212] 
%-----------------------------------解Y-W方程，得偏相关函数X-------------------------------------%
figure; 
plot(X);
title('偏相关函数图');
pause 

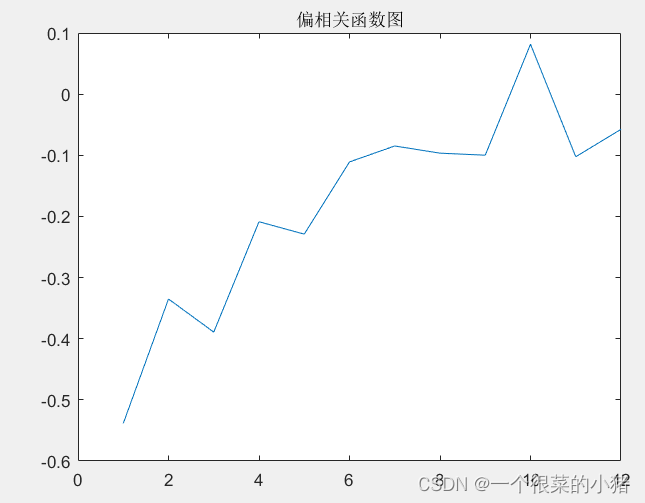
6、应用AIC准则为模型定阶

%-----根据偏相关函数截尾性，初判模型阶次为5。用最小二乘法估计参数,计算10阶以内的模型残差方差和AIC值，应用AIC准则为模型定阶------%S=[R0 R(1) R(2) R(3) R(4)];G=toeplitz(S);W=inv(G)*[R(1:5)]'                      % 参数W(i) 与X5相同K=0;                              for t=6:88r=0; for i=1:5r=W(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K;                                                     endU(5)=K/(88-5)                        % 5阶模型残差方差 0.4420K=0;T=X1;
for t=2:88at=Y(t)-T(1)*Y(t-1);K=(at)^2+K; 
end                        U(1)=K/(89-1)                         % 1阶模型残差方差0.6954           K=0;T=X2;for t=3:88                                                      r=0; for i=1:2r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(2)=K/(88-2)                     % 2阶模型残差方差 0.6264  K=0;T=X3;for t=4:88r=0; for i=1:3r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(3)=K/(88-3)                      % 3阶模型残差方差 0.5327K=0;T=X4;for t=5:88r=0; for i=1:4r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(4)=K/(88-4)                     % 4阶模型残差方差  0.4751 K=0;T=X6;for t=7:88r=0; for i=1:6r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(6)=K/(88-6)                     % 6阶模型残差方差 0.4365 K=0;T=X7;for t=8:88                                            r=0; for i=1:7r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(7)=K/(88-7)                     % 7阶模型残差方差 0.4331K=0;T=X8;for t=9:88r=0; for i=1:8r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(8)=K/(88-8)                     % 8阶模型残差方差0.4310 K=0;T=X9;for t=10:88r=0; for i=1:9r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(9)=K/(88-9)                     %9阶模型残差方差 0.4297K=0;T=X10;for t=11:88r=0; for i=1:10r=T(i)*Y(t-i)+r;endat= Y(t)-r;K=(at)^2+K; endU(10)=K/(88-10)                   % 10阶模型残差方差 0.4317 U=10*Ufor i=1:10AIC2(i)=88*log(U(i))+2*(i)        % AIC值分别为：172.6632  165.4660  153.2087  145.1442  140.7898  141.6824  142.9944  144.5601  146.3067  148.7036end

取使得AIC值为最小值的阶次，判断模型阶次为5，用最小二乘法估计参数。

7、 预测

%------------------检验{at}是否为白噪声。求{at}的自相关系数，看其是否趋近于零-----------------------%C=0;K=0;for t=7:88at=Y(t)-W(1)*Y(t-1)-W(2)*Y(t-2)-W(3)*Y(t-3)-W(4)*Y(t-4)-W(5)*Y(t-5)+Y(6)-W(1)*Y(5)-W(2)*Y(4)-W(3)*Y(3)-W(4)*Y(2)-W(5)*Y(1);at1=Y(t-1)-W(1)*Y(t-2)-W(2)*Y(t-3)-W(3)*Y(t-4)-W(4)*Y(t-5)-W(5)*Y(t-6);C=at*at1+C;K=(at)^2+K; 
endp=C/K              %若p接近于零，则{at}可看作是白噪声                 %--------------------------------{at}的自相关系数,趋近于零，模型适用--------------------------------%%------------AR(5)模型方程为------------------------------------------------------------------------%% X(t)=W(1)*X(t-1)-W(2)*X(t-2)-W(3)*X(t-3)-W(4)*X(t-4)-W(5)*X(t-5)+at     (at=0.4420)%------------------------------------------后六年的数据 进行预测和效果检验----------------------------------------------%%-----------------------------单步预测  预测当前时刻后的六个数据----------------------------------%XT=[L(84:94)]; for t=6:11m(t)=0;for i=1:5m(t)=W(i)*XT(t-i)+m(t);  endendm=m(6:11);%-------------预测值进行反处理---------------%m(1)=Yt(90)+m(1);            %一次反差分z1(1)=P(90)+m(1);            %二次反差分m(2)=Yt(91)+m(2);z1(2)=P(91)+m(2);  m(3)=Yt(92)+m(3);z1(3)=P(92)+m(3); m(4)=Yt(93)+m(4);z1(4)=P(93)+m(4); m(5)=Yt(94)+m(5);z1(5)=P(94)+m(5); m(6)=Yt(95)+m(6);z1(6)=P(95)+m(6); z1                                               % 单步预测的向后6个预测值:z1= 13.9423   13.4101   13.3588   12.9856   13.2594   12.9552%---------------------------绘制数据模型逼近曲线-----------------------------------%for  t=6:88r=0; for i=1:5r=W(i)*Y(t-i)+r;endat= Y(t)-r;    
end figure;
for t=6:88y(t)=0;for i=1:5y(t)=W(i)*Y(t-i)+y(t);  endy(t)=y(t)+at;y(t)=Yt(t+1)-y(t);y(t)=P(t+1)-y(t);
end
plot(y,'r-*');                    % 样本数据模型逼近曲线
hold on;
plot(91:96,z1,'r-*'); 
hold on;
plot(P,'--');                     % 原样本曲线
title('AR(5)模型样本逼近预测曲线');
pause  
%-----------------------------绘制数据模型逼近曲线-----------------------------------% %-------------------------预测误差分析------------------------%%-----------计算单步预测绝对误差-------------%D=[13.70 13.66 13.27 13.56 13.14  14.19 ];                   for i=1:6                                         e1(i)=D(i)-z1(i);PE1(i)= (e1(i)/D(i))*100;                                                      end e1                                                 % 单步预测的绝对误差 e1 =  -0.2423    0.2499   -0.0888    0.5744   -0.1194    1.2348PE1%------单步预测平均绝对误差-------------------%                                           
mae1=sum(abs(e1)) /6                                   % mae1 = 0.2681%------单步预测平均绝对百分比误差-------------------%    
MAPE1=sum(abs(PE1))/6%------绘制预测结果和实际值的比较图-----------%
figure;
plot(1:6,D,'-+') ;                    
hold on;
plot(z1,'r-*');
title('向前一步预测值和实际值对比图');
hold off;
pause  
%--------------------------------单步预测  预测当前时刻后的六个数据---------------------------------%%----------------------------------多步预测 目的是向前六步预测--------------------------------------%
Xt=[ Y(84) Y(85) Y(86) Y(87) Y(88)];           %取当前时刻之前的6个数据Z(1)=W(1)*Xt(5)+W(2)*Xt(4)+W(3)*Xt(3)-W(4)*Xt(2)-W(5)*Xt(1)                                 
%------求向前l步的预测值 %预测步数小于5时for l=2:5K(l)=0; for i=1:l-1  K(l)=W(i)*Z(l-i)+K(l); endG(l)=0;for j=l:5G(l)=W(j)*Xt(5+l-j)+G(l);endZ(l)=K(l)+G(l);end%预测步数大于5时（向前6步预测）for l=6:6K(l)=0; for i=1:5K(l)=W(i)*Z(l-i)+K(l); endZ(l)=K(l);end%----预测值进行反标准化处理r=Z*v+Ux                   %  0.0581    0.0844    0.0156    0.0319    0.0632    0.0652r(1)=Yt(90)+r(1);           %一次反差分z(1)=P(90)+r(1)             %二次反差分for i=2:6r(i)=r(i-1)+r(i);z(i)=z(i-1)+r(i)  end%---------------------------- 预测误差分析 ------------------------------%
%-------计算绝对误差和相对误差 
D=[13.70 13.66 13.27 13.56 13.14  14.19 ];         % 预测值 z =14.0281   13.9606   13.9087   13.8887   13.9318   14.0403               for i=1:6                                         e6(i)=D(i)-z(i); PE6(i)= (e6(i)/D(i))*100;                                                        end e6                                                % 多步预测的绝对误差 e = -0.3281    -0.3006   -0.6387   -0.3287   -0.7918    0.1497PE6                                              % 多步预测的相对误差1-abs(PE6)                                          % 准确率%------多步预测平均绝对误差                                          
mae6=sum(abs(e6)) /6  %------多步预测平均绝对百分比误差                                          
MAPE6=sum(abs(PE6))/6%------绘制预测结果和实际值的比较图
figure;
plot(1:6,D,'-+')                     
hold on;
plot(z,'r-*');
title('向前六步预测值和实际值对比图');
hold off;