【算法自由之路】二叉树的递归套路

预热，二叉树的后继节点

话不多说，首先是一道练手题，寻找二叉树任意给定节点的后继节点，此二叉树具备一个指向父节点的指针。

后继节点：在中序遍历中于给定节点后一个打印的节点

    public static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode parent;public TreeNode(int val) {this.val = val;}}

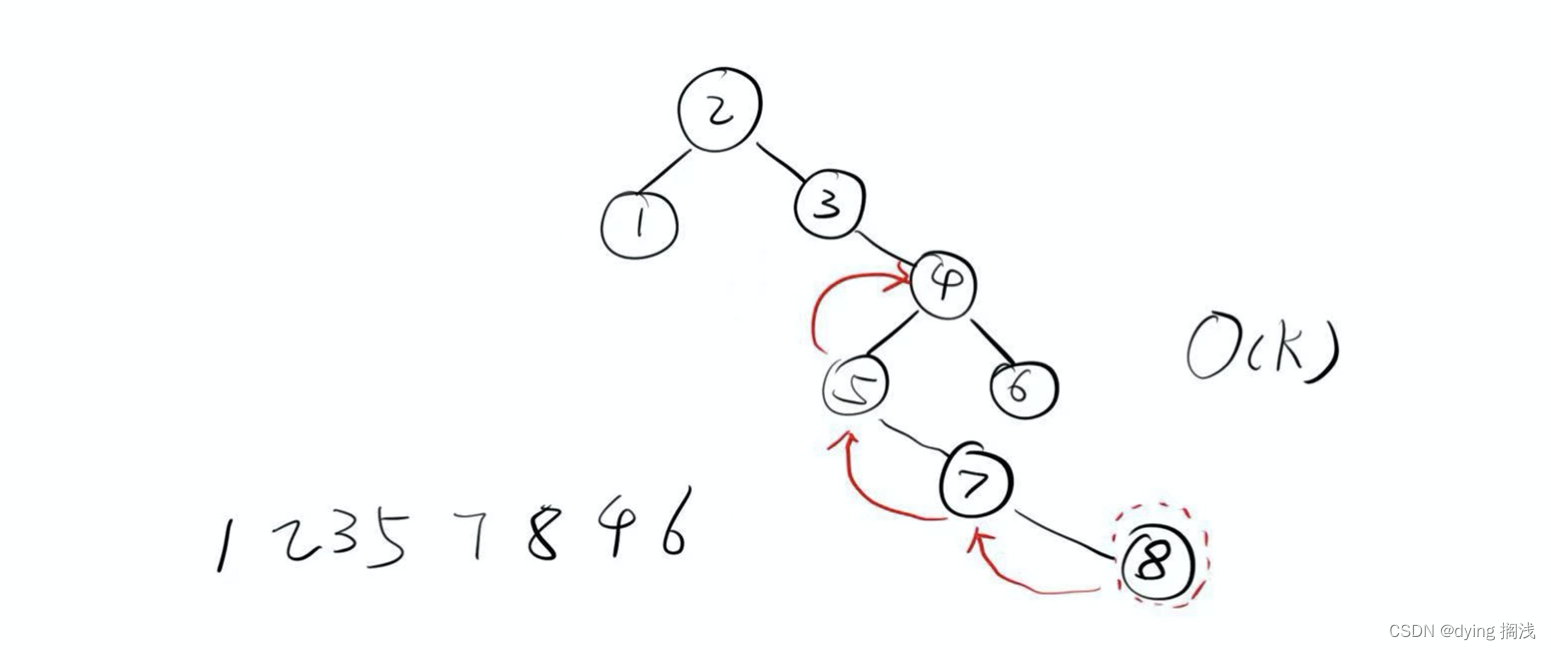
这道题其实主要考验的是分类讨论和找规律的能力。首先理解中序遍历对每个子树打印顺序都是 左 中 右。比如下图这个树

做分类讨论其实就两个情况：

1. 该节点有右节点：后继为右节点的最左节点
2. 该节点没有右节点：后继节点为向上找，第一次子节点是父节点的左孩子的父节点，比如 8 的后继就是 4

对于情况 2 我们其实可以反推来理解， 4 节点的前驱节点应该是 左子树的最右的一个节点。

package algorithmic.base.tree;/*** @program: algorithmic-total-solution* @description: 查找二叉树的后继节点，* @author: wangzibin* @create: 2023-01-10**/
public class FindNextNode {public static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode parent;public TreeNode(int val) {this.val = val;}@Overridepublic String toString() {return "TreeNode{" +"val=" + val +'}';}}public static void print(TreeNode node) {if (node == null) {return;}print(node.left);System.out.print(node.val);print(node.right);}public static TreeNode findNextNode(TreeNode node) {if (node == null) {return null;}TreeNode result = null;// 如果有右孩子，后继节点是右孩子的最左节点if (node.right != null) {result = node.right;while (result.left != null) {result = result.left;}return result;}// 如果没有右孩子,向上找第一个子孩子是左节点的父节点 （有点绕，看代码）result = node.parent;// 注意最右节点没有后继节点while (node.parent != null && node != result.left) {node = node.parent;result = node.parent;}return result;}public static void main(String[] args) {TreeNode head = new TreeNode(2);TreeNode node1 = new TreeNode(1);TreeNode node3 = new TreeNode(3);TreeNode node4 = new TreeNode(4);TreeNode node5 = new TreeNode(5);TreeNode node6 = new TreeNode(6);TreeNode node7 = new TreeNode(7);TreeNode node8 = new TreeNode(8);head.left = node1;node1.parent = head;head.right = node3;node3.parent = head;node3.right = node4;node4.parent = node3;node4.left = node5;node5.parent = node4;node4.right = node6;node6.parent = node4;node5.right = node7;node7.parent = node5;node7.right = node8;node8.parent = node7;print(head);System.out.println();System.out.println(findNextNode(node1));System.out.println(findNextNode(head));System.out.println(findNextNode(node3));System.out.println(findNextNode(node5));System.out.println(findNextNode(node7));System.out.println(findNextNode(node8));System.out.println(findNextNode(node4));System.out.println(findNextNode(node6));}}

递归套路

二叉树的递归套路有点像拆分子任务，将要求的最终结果分给每个分支去做

在实际应用中，对于一个整个树的问题，假设可以向左右子树要任何信息，整合信息后得出最终结果

整个拆分任务的操作我们交给了堆栈去做

递归套路 1 判断一个二叉树是平衡二叉树

平衡二叉树定义：对于树中任意一个节点，其左子树和右子树的高度差不超过 1。

这里假设我可以向左右子树获取任何信息，那对于判断我是否是平衡二叉树的关系信息是：

1. 子树高度
2. 子树是否是平衡二叉树

于是我可以定义这样一个返回结构

    public static class NodeInfo {public boolean isBalanced;public int high;public NodeInfo(boolean isBalanced, int high) {this.isBalanced = isBalanced;this.high = high;}}

最终代码很简单

public class BalanceTree {public static class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}public static class NodeInfo {public boolean isBalanced;public int high;public NodeInfo(boolean isBalanced, int high) {this.isBalanced = isBalanced;this.high = high;}}public boolean isBalanced(TreeNode root) {return getNodeInfo(root).isBalanced;}public NodeInfo getNodeInfo(TreeNode node) {if (node == null) {return new NodeInfo(true, 0);}// 获取左子树信息NodeInfo left = getNodeInfo(node.left);// 获取右子树信息NodeInfo right = getNodeInfo(node.right);// 如果左右子树都平衡且高度差为 1 则我也平衡boolean isBalanced = left.isBalanced && right.isBalanced && Math.abs(left.high - right.high) <= 1;// 我的高度为左右子树最大高度 +1int high = Math.max(left.high, right.high) + 1;return new NodeInfo(isBalanced, high);}}

可以直接到 leetcode 验证 平衡二叉树

感受到二叉树的递归套路的魅力了吗？关键点在于：

1. 思考 当前 节点 与 左右子节点的关系 （一般的我们可以以 以 与当前节点有关 和 与当前节点无关 来进行分类讨论 ）
2. 向左右子节点获取什么信息能够计算出我的信息
3. 整合信息，定义结构

递归套路 2 计算给定树结构中二叉搜索子树的最大键和值

首先定义二叉搜索数 ： 对于树中任意一个节点，其左树都小于该节点，右树都大于该节点

需要向左右节点要的信息：

1. 树的最大值
2. 树的最小值
3. 是否是二叉搜索树
4. 当前树的键和值
5. 二叉搜索子树的最大键和值

在递归中就需要讨论最终结果是否与当前节点有关了，直接看代码

package algorithmic.base.tree;import javax.xml.soap.Node;/*** @program: algorithmic-total-solution* @description: 二叉搜索子树最大键和值  https://leetcode.cn/problems/maximum-sum-bst-in-binary-tree/* @author: wangzibin* @create: 2023-01-11**/
public class MaxSumBST {public static class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}public static class NodeInfo {// 当前节点子树最大值private int max;private int min;private boolean isBst;private int bstSum;private int bstMaxSum;@Overridepublic String toString() {return "NodeInfo{" +"max=" + max +", min=" + min +", isBst=" + isBst +", bstSum=" + bstSum +", bstMaxSum=" + bstMaxSum +'}';}}public static NodeInfo getInfo(TreeNode node) {if (node == null) {NodeInfo empty = new NodeInfo();empty.isBst = true;empty.min = Integer.MAX_VALUE;empty.max = Integer.MIN_VALUE;return empty;}NodeInfo leftInfo = getInfo(node.left);NodeInfo rightInfo = getInfo(node.right);NodeInfo current = new NodeInfo();current.max = max(node.val, leftInfo.max, rightInfo.max);current.min = min(node.val, leftInfo.min, rightInfo.min);// 判断是否与我有关, 当且仅当我也是二叉搜索树时最大值才与我有关，否则只需要比较子树值即可if (leftInfo.isBst && rightInfo.isBst && leftInfo.max < node.val && rightInfo.min > node.val) {// 左右子树都是搜索树，且 左子树最大值 小于 当前节点值 ，右子树最小值 大于 当前节点值，则可讨论与当前节点有关的情况current.isBst = true;current.bstSum = node.val + leftInfo.bstSum + rightInfo.bstSum;current.bstMaxSum = max(current.bstSum, leftInfo.bstMaxSum, rightInfo.bstMaxSum);} else {current.isBst = false;current.bstMaxSum = Math.max(leftInfo.bstMaxSum, rightInfo.bstMaxSum);}return current;}public static int max(int num1, int num2, int num3) {return Math.max(Math.max(num1, num2), num3);}public static int min(int num1, int num2, int num3) {return Math.min(Math.min(num1, num2), num3);}public static int maxSumBST(TreeNode root) {if (root == null) {return 0;}int bstMaxSum = getInfo(root).bstMaxSum;return Math.max(bstMaxSum, 0);}public static void main(String[] args) {TreeNode treeNode1 = new TreeNode(1);treeNode1.left = null;TreeNode treeNode10 = new TreeNode(10);TreeNode treeNode5 = new TreeNode(-5);TreeNode treeNode20 = new TreeNode(20);treeNode1.right = treeNode10;treeNode10.left = treeNode5;treeNode10.right = treeNode20;System.out.println(maxSumBST(treeNode1));}}

验证正确性 1373. 二叉搜索子树的最大键值和