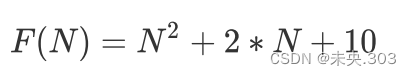【数据结构初阶】第一节.初识时间和空间复杂度
文章目录
前言
一、认识数据结构
二、时间复杂度
2.1 时间复杂度的概念
2.2 计算时间复杂度
2.2.1 大O的渐进表示法
2.3 常见时间复杂度计算举例
三、空间复杂度
3.1 空间复杂度的概念
3.2 计算空间复杂度
3.3 常见空间复杂度计算举例
四、常见复杂度的对比;
总结
前言
今天我们就将进入到数据结构与算法的内容当中,数据结构作为程序员必须掌握的四大件之一,是非常重要的内容,也是一大难点,也是我们必须熟练的掌握的内容;今天就让我们先初步的认识它吧!!!!!!!!!!!!!!!
提示:以下是本篇文章正文内容,下面案例可供参考
一、认识数据结构
数据结构全称数据结构与算法;

定义:
数据结构:是一门单独的学科,他和语言没有关系。
数据+结构:用来描述和组织数据的方式。
特点:
数据结构有以下特点:
1、逻辑非常严谨;
2、代码量是非常多的;
3、调试是必不可少的;
注意:
在学习数据结构中,一定要多思考,多画图,多写代码;

二、时间复杂度
2.1 时间复杂度的概念
概念:
算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间;
一个算 法所花费的时间与其中语句的执行次数成正比例; 所以算法中的基本操作的执行次数,为算法的时间复杂度。
常见的时间复杂度排序:
O(1)< O(log2(n))< O(n)< O(nlog2(n)< O(n^2)< O(n^3)< O(2^n)< O(n!)< O(n^n)
说明:
一般来说,到了O(n^2)及以上数据量大时运行效率极低,所以数据量大时,应选用更有的算法;
2.2 计算时间复杂度
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们 使用大O的渐进表示法。
2.2.1 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号;
方法的使用规则:
1、用常数1取代运行时间中的所有加法常数。 2、在修改后的运行次数函数中,只保留最高阶项。 3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
代码举例说明:
代码如下:
计算一下下面代码中func1执行了多少次???
// 请计算一下func1基本操作执行了多少次? void func1(int N){ int count = 0; for (int i = 0; i < N ; i++) { for (int j = 0; j < N ; j++) { count++; } } for (int k = 0; k < 2 * N ; k++) { count++; } int M = 10; while ((M--) > 0) { count++; } System.out.println(count); }经过分析可知:
执行次数:
此时当我们使用大O的渐进表示法以后得到其执行次数:
执行次数:
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界) 平均情况:任意输入规模的期望运行次数; 最好情况:任意输入规模的最小运行次数(下界)
举例说明: 例如:在一个长度为N数组中搜索一个数据x 最好情况:1次找到 最坏情况:N次找到 平均情况:N/2次找到 在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3 常见时间复杂度计算举例
示例1:
// 计算func2的时间复杂度? void func2(int N) {int count = 0;for (int k = 0; k < 2 * N ; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count); }解析:
第一个for循环执行2N次,while循环执行10次,则
经过大O的渐进表示法后,为
示例2:
代码2:
// 计算func3的时间复杂度? void func3(int N, int M) {int count = 0;for (int k = 0; k < M; k++) {count++;}for (int k = 0; k < N ; k++) {count++;}System.out.println(count); }解析:
第一个for循环执行M次;第二个for循环执行N次;
故F(n)=M+N;
经过大O的渐进表示法后,为O(M+N);
示例3:
冒泡排序的时间复杂度
代码3:
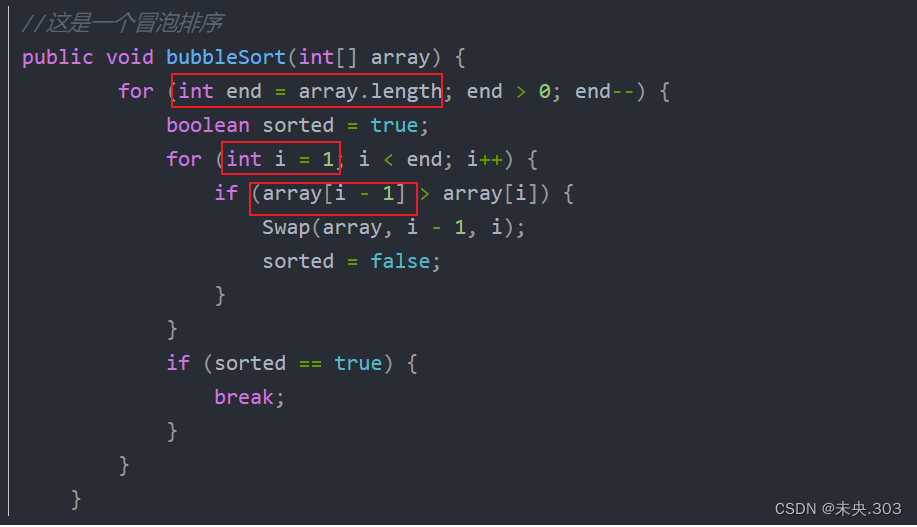
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}} }解析:
冒泡排序基本操作执行最好N次,最坏执行了(N*(N-1))/2次,通过推导大O阶方法+时间复杂度一般看最坏, 时间复杂度为 :
示例4:
计算binarySearch(二分查找)的时间复杂度
代码4:
int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1; }解析:
基本操作执行最好1次,最坏O(log(2)N)次,时间复杂度为:

三、空间复杂度
3.1 空间复杂度的概念
概念:
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。 一个程序的空间复杂度是指运行完一个程序所需内存的大小;
3.2 计算空间复杂度
空间复杂度的计算同样要用大O渐进表示法;上面已经介绍过了,此处就不一一赘述了;
3.3 常见空间复杂度计算举例
示例1:
代码1:
public void function() {int a[] = { 1, 2, 3, 4, 5 };int tmp = 0;for (int i = 0; i < (a.length / 2); i++) {tmp = a[i];a[i] = a[a.length - i - 1];a[a.length - i - 1] = tmp;}System.out.println(Arrays.toString(a)); }解析:
这是一段很具有迷惑性的代码,虽然看上去有for循环也定义了一个a数组,但是我们再仔细看看代码中都是常量定义的,所以这段代码的空间复杂度实则为O(1).
示例2:
冒泡排序法的空间复杂度
代码2:
//这是一个冒泡排序 public void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}解析:
为了完成这个算法我们在函数中,只开辟了3个变量的内存空间,为常数项,所以冒泡排序法的空间复杂度是O(1).
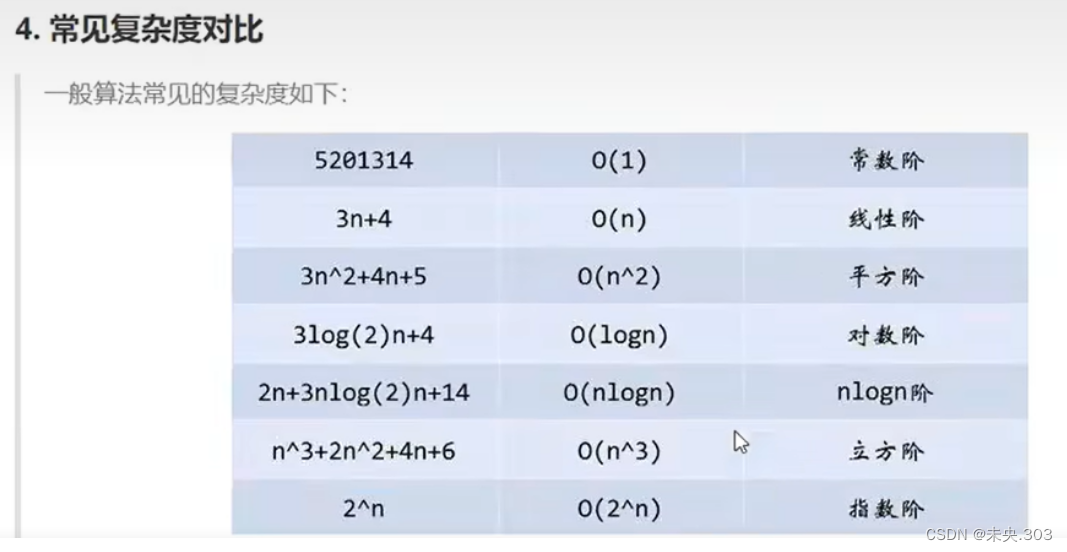
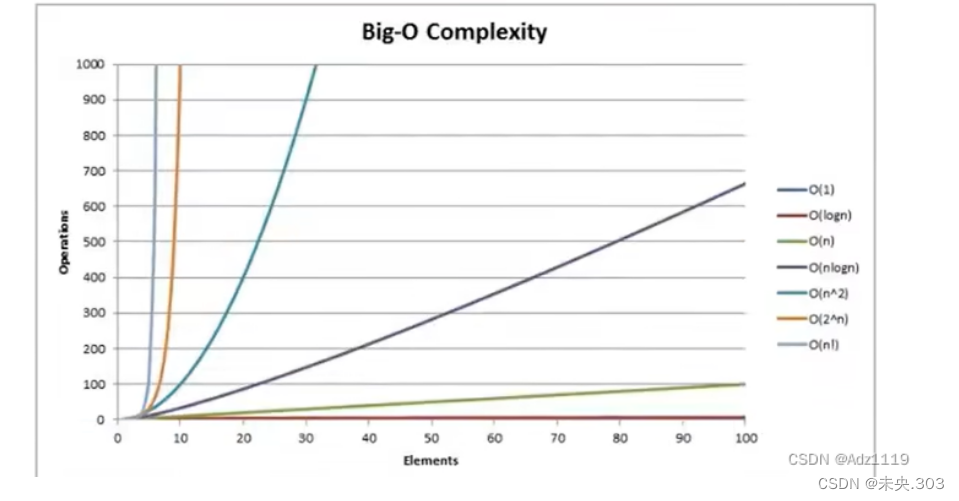
四、常见复杂度的对比;
总结
今天的内容就分享到这里了,我们下一节内容再见!!!!!!!!!