快速傅里叶算法(FFT)快在哪里?
目录
前言
1、DFT算法
2、FFT算法
2.1 分类
2.2 以基2 DIT(时间抽取) FFT 算法为例
2.2.1 一次分解
2.2.2 多次分解
参考
前言
对信号分析的过程中,为了能换一个角度观察问题,很多时候需要把时域信号波形变换到频域进行分析,这涉及到对信号求傅里叶变换,在计算机中便于处理的是离散信号,因此需要求信号的离散傅里叶变换,但是离散傅里叶变换(DFT--Discrete Fourier transform)的算法时间复杂度O(n2),为了能提高计算的速度,很多时候我们进行的变换为快速傅里叶变换(FFT--Fast Fourier Transform),其算法时间复杂度O(nlogn),大大提高了计算的速度,那么该快速傅里叶变换算法的快在哪里?中间进行了什么操作,我们下面具体分析。
在之前的一篇文章中我们提到了DFT和FFT的关系
频谱、功率谱、倒频谱_heda3的博客-CSDN博客_倒频谱
1、DFT算法
DFT的数学计算表达式为:
长度为N的离散时间信号x(n),做N点离散傅里叶变换如下:
其中k=0,1,2,...N-1
其中
运算量表述为:
依据上述公式可知,做1点DFT,需要N次复数乘法、N-1次复数加法
做N点DFT,则需要N*N次复数乘法、N*(N-1)次复数加法
当N为256点时,所需运算量65536次复数乘法、65280次复数加法
N=512点时,所需运算量262144次复数乘法、261632次复数加法
N=1024点时,所需运算量1048576次复数乘法、1047552次复数加法
可见当N点从256到1024点变化时,DFT算法的计算量从万级到百万级。
2、FFT算法
2.1 分类
分为按照时间抽取(在时间上将信号长度逐步减少)和按照频率抽取
依据抽取长度分为基2、基4
基2 DIT(时间抽取) FFT 也称为Cooley-Tukey algorithm 库利图基算法
基2 DIF(频率抽取) FFT
基4 FFT
分裂基FFT(包含两种不同基的混合计算)
2.2 以基2 DIT(时间抽取) FFT 算法为例
基于基2时间抽取将信号划分为两部分分别计算FFT(信号长度N要求为N=2的整数倍):
1)
其中k=0,1,2,...N-1
复数运算的特性
对称性:
周期性:
可约性:
常见的计算
2.2.1 一次分解
依据上述复数运算的特性的可约性,则1)化简为:
2)
3)
其中k=0,1,2,...N-1
利用特性:
则3)可表述为:
4)
其中k=0,1,2,...N/2-1
用如下的蝶形方式表述为3式和4式:
两次复数运算:
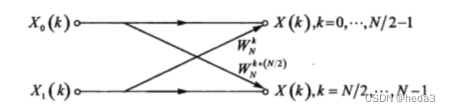
一次复数运算:
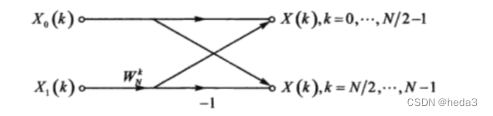
也即是N点DFT包含:2个 N/2点DFT和N/2个蝶形运算,一个蝶形运算包含一次复数乘法和两次复数加法
上述:做N点DFT,则需要N*N次复数乘法、N*(N-1)次复数加法
则2个N/2点DFT,则需要2*(N/2*N/2)=/2次复数乘法,2*(N/2)*(N/2-1)=N(N/2-1)次复数加法运算;蝶形运算次数:N/2次复数乘法,N次复数加法。
因此总的复数乘法计算:N(N+1)/2 总的复数加法次数:/2
通过上述的一次分解前后的运算量分析,可见经过一次分解后(信号按照奇偶数将N点DFT划分为N/2点DFT,并将两个N/2点DFT组合的方式),其运算量降低了一半,计算效率得到了提升。
2.2.2 多次分解
当N一直分解下去直到DFT的点数为2时,最小的计算单元为一个基本的蝶形运算,因此由于信号长度最初定义为N=2的整数倍,也即是N=,因此N点DFT运算可以分解为M级蝶形运算,每一级为N/2个蝶形运算。
通过上述的FFT计算方法,则N点FFT运算需要M*N/2个蝶形运算,复数乘法次数:
复数加法次数:
当N点从256到1024点变化时,FFT算法的计算量从千级到万级。可见FFT运算速度较DFT得到较大的提升。
现在我们可以明显知道FFT到底快在哪里,因为经过对信号的逐级分解,将大点DFT划分为小点DFT计算,也即是N点FFT若基于基2抽取方法,则需要级分解,N点DFT最终划分为2点DFT计算,并结合指数运算的特性,减少冗余计算,使得运算量大为减小。
参考
【1】《数字信号处理》
【2】如何利用FFT(基2时间以及基2频率)信号流图求序列的DFT
