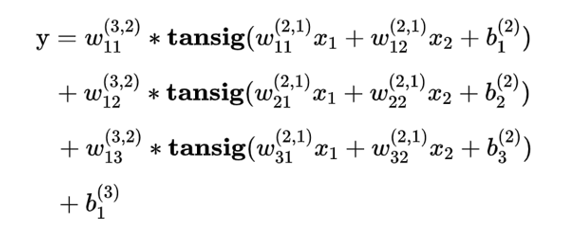BP神经网络的梯度公式推导(三层结构)_民生

BP神经网络的梯度公式推导(三层结构)

创始人

2024-05-26 19:41:11

0次

本站原创文章，转载请说明来自《老饼讲解-BP神经网络》bp.bbbdata.com

一. 推导目标

1.1 梯度公式目标

1.2 本文梯度公式目标

二. 网络表达式梳理

2.1 梳理三层BP神经网络的网络表达式

三. 三层BP神经网络梯度推导过程

3.1 简化推导目标

3.2 输出层权重的梯度推导

3.3 输出层阈值的梯度推导

3.4隐层权重的梯度推导

3.5 隐层阈值的梯度推导

四. 推导结果总结

4.1 三层BP神经网络梯度公式

BP神经网络的训练算法基本都涉及到梯度公式，

本文提供三层BP神经网络的梯度公式和推导过程

一. 推导目标

BP神经网络的梯度推导是个复杂活，

在推导之前，本节先把推导目标清晰化

1.1 梯度公式目标

训练算法很多，但各种训练算法一般都需要用到各个待求参数(w,b)在损失函数中的梯度，
因此求出w,b在损失函数中的梯度就成为了BP神经网络必不可少的一环，

求梯度公式，即求以下误差函数E对各个w,b的偏导：
$\displaystyle \displaystyle \textbf{E}(W,b)=\dfrac{1}{M}\sum \limits _{m=1}^{M} \dfrac{1}{K}\sum \limits _{k=1}^{K} (\textbf{f}(\textbf{x})_{km}-\text{y}_{km})^2$

$\textbf{f}(\textbf{x})_{km}$ 代表网络对第m个样本第k个输出的预测值，w,b就隐含在 $\textbf{f}(\textbf{x})$ 中

1.2 本文梯度公式目标

虽然梯度只是简单地求E对w,b的偏导，但E中包含网络的表达式f(x)，就变得非常庞大，
求偏导就成了极度艰巨晦涩的苦力活，对多层结构通式的梯度推导稍为抽象，
本文不妨以最常用的三层结构作为具体例子入手，求出三层结构的梯度公式
即：输入层-隐层-输出层 (隐层传递函数为tansig,输出层传递函数为purelin)

虽然只是三层的BP神经网络，

但梯度公式的推导，仍然不仅是一个体力活，还是一个细致活，

且让我们细细一步一步慢慢来

二. 网络表达式梳理

在损失函数E中包括了网络表达式，在求梯度之前，

先将表达式的梳理清晰，有助于后面的推导

2.1 梳理三层BP神经网络的网络表达式

网络表达式的参考形式
隐层传递函数为tansig,输出层传递函数为purelin的三层BP神经网络，
有形如下式的数学表达式

网络表达式的通用矩阵形式
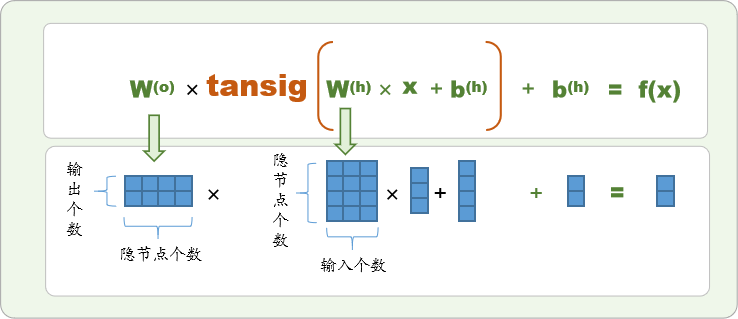
写成通用的矩阵形式为

$\textbf{f}(\textbf{x}) = \textbf{W}^{(o)}\textbf{tansig}(\textbf{W}^{(h)}\textbf{x}+\textbf{b}^{(h)})+\textbf{b}^{(o)}$

这里的 $\textbf{W}$ 为矩阵， $\textbf{x}$ 和 $\textbf{b}$ 为向量，
上标(o)和(h)分别代表输出层(out)和隐层(hide)，

例如，2输入，4隐节点，2输出的BP神经网络可以图解如下：

三. 三层BP神经网络梯度推导过程

本节我们具体推导误差函数对每一个待求参数w,b的梯度

3.1 简化推导目标

由于E的表达式较为复杂，
不妨先将问题转化为"求单样本梯度"来简化推导表达式
对于任何一个需要求偏导的待求参数w,都有: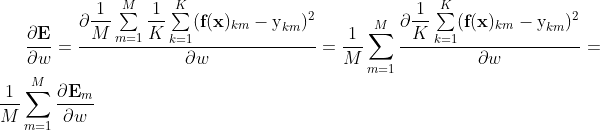
$\displaystyle \dfrac{\partial \textbf{E}}{\partial w} = \dfrac{\partial \dfrac{1}{M}\sum \limits _{m=1}^{M} \dfrac{1}{K}\sum \limits _{k=1}^{K} (\textbf{f}(\textbf{x})_{km}-\text{y}_{km})^2 }{\partial w} =\dfrac{1}{M}\sum \limits _{m=1}^{M}\dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_{km}-\text{y}_{km})^2 }{\partial w} = \dfrac{1}{M}\sum \limits _{m=1}^{M}\dfrac{\partial \textbf{E}_m}{\partial w}$

即损失函数的梯度，等于单个样本的损失函数的梯度之和（E对b的梯度也如此），
因此，我们先推导单个样本的梯度，最后再对单样本梯度求和即可。
现在问题简化为求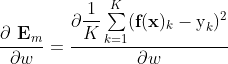
$\dfrac{\partial\textbf{ E}_m}{\partial w} = \dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})^2 }{\partial w}$

3.2 输出层权重的梯度推导

输出层权重梯度推导
输出层的权重为"输出个数*隐节点个数"的矩阵,
现推导任意一个权重wji (即连接第i个隐层与第j个输出的权重)的单样本梯度
如下：
$\displaystyle \begin{aligned} \dfrac{\partial\textbf{ E}_m}{\partial w_\textbf{ji}^{(o)}} &= \dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_\textbf{k}-\text{y}_\textbf{k})^2 }{\partial w_\textbf{ji}^{(o)}} \\&= \dfrac{1}{K}\sum \limits _{k=1}^{K}\dfrac{\partial (\textbf{f}(\textbf{x})_\textbf{k}-\text{y}_\textbf{k})^2 }{\partial w_\textbf{ji}^{(o)}} \\&= \dfrac{1}{K}\sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_\textbf{k}-\text{y}_\textbf{k})\dfrac{\partial \textbf{f}(\textbf{x})_\textbf{k} }{\partial w_\textbf{ji}^{(o)}} \end{aligned}$
事实上，只有第j个输出 $\textbf{f(x)}_\textbf{j}$ 是关于 $w_\textbf{ji}^{(o)}$ 的函数，也即对于其它输出 $\dfrac{\partial \textbf{f}(\textbf{x})_{k(k\ne j )} }{\partial W} = 0$
因此，
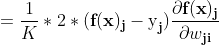
上式即等于 $= \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \textbf{f}(\textbf{x})_\textbf{j} }{\partial w_\textbf{ji}}$

继续求导
$\displaystyle \begin{aligned} & \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \textbf{f}(\textbf{x})_\textbf{j} }{\partial w_\textbf{ji}^{(o)}} \\=& \color{blue}\dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \left ( w_\textbf{j1}^{(o)}*\textbf{tansig}_\textbf{1}+...+w_\textbf{ji}^{(o)}*\textbf{tansig}_\textbf{i}+...+w_\textbf{jh}^{(o)}*\textbf{tansig}_\textbf{h}+b_\textbf{j}^{(o)} \right ) }{\partial w_\textbf{ji}^{(o)}} \\= &\dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})*\textbf{tansig}_\textbf{i} \end{aligned}$
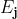
$\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j}$ 是第j个输出的误差，简记为 $E_\textbf{j}$
$\textbf{tansig}_\textbf{i}$ 是第j个隐节点的激活值，简记为 $A_\textbf{i}$ （A即Active）

上式即可写为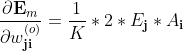
$\dfrac{\partial \textbf{E}_m}{\partial w_\textbf{ji}^{(o)}} = \dfrac{1}{K}* 2 *E_\textbf{j}*A_\textbf{i}$

上述是单样本的梯度，
整体样本的梯度则应记为
$\displaystyle \dfrac{\partial \textbf{E}}{w_\textbf{ij}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} 2 *E_\textbf{jm}*A_\textbf{im}$

M,K为样本个数、输出个数
$E_\textbf{jm}=\textbf{f}(\textbf{x})_\textbf{jm}-\text{y}_\textbf{jm}$ 是第m个样本第j个输出的误差
$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值

3.3 输出层阈值的梯度推导

输出层阈值梯度推导
对于阈值 $b_\textbf{j}^{(o)}$ (第j个输出节点的阈值)的推导与权重梯度的推导是类似的，
只是上述标蓝部分应改为

$\displaystyle \begin{aligned} \dfrac{\partial \textbf{E}_{m} }{\partial b_\textbf {j}^{(o)}} &= \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j})\dfrac{\partial \left ( w_\textbf{j1}^{(o)}*\textbf{tansig}_\textbf{1}+...+w_\textbf{ji}^{(o)}*\textbf{tansig}_\textbf{i}+...+w_\textbf{jh}^{(o)}*\textbf{tansig}_\textbf{h}+b_\textbf{j}^{(o)} \right ) }{\partial b_\textbf{j}^{(o)}} \\&= \dfrac{1}{K}* 2 *(\textbf{f}(\textbf{x})_\textbf{j}-\text{y}_\textbf{j}) \end{aligned}$
简记为
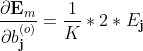
$\dfrac{\partial \textbf{E}_m}{\partial b_\textbf{j}^{(o)}} =\dfrac{1}{K}* 2 *E_\textbf{j}$

上述是单样本的梯度，
整体样本的梯度则应记为
$\dfrac{\partial \textbf{E}}{\partial b_\textbf{j}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M}* 2 *E_\textbf{jm}$
M,K为样本个数、输出个数
$E_\textbf{jm}=\textbf{f}(\textbf{x})_\textbf{jm}-\text{y}_\textbf{jm}$ 是第m个样本第j个输出的误差

3.4隐层权重的梯度推导

隐层的权重为"隐节点个数*输入个数"的矩阵,
现推导任意一个权重 $w_\textbf{ji}^{(h)}$ (即连接第i个输入与第j个隐节点的权重)的单样本梯度
如下：
$\displaystyle \begin{aligned} \dfrac{\partial\textbf{ E}_m}{\partial w_\textbf{ji}^{(h)}} &= \dfrac{\partial \dfrac{1}{K}\sum \limits _{k=1}^{K}(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})^2 }{\partial w_\textbf{ji}^{(h)}} \\&= \dfrac{1}{K} \sum \limits _{k=1}^{K}\dfrac{\partial (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})^2 }{\partial w_\textbf{ji}^{(h)}} \\&= \dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \textbf{f}(\textbf{x})_{k} }{\partial w_\textbf{ji}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \left ( w_\textbf{k1}^{(o)}*\textbf{tansig}_\textbf{1}+...w_\textbf{kj}^{(o)}*\textbf{tansig}_\textbf{j}+...+w_\textbf{kh}^{(o)}*\textbf{tansig}_\textbf{h}+b_\textbf{k}^{(o)} \right ) }{\partial w_\textbf{ji}^{(h)}} \end{aligned}$

只有第j个tansig是关于 $w_\textbf{ji}^{(h)}$ 的函数，所以上式可以写成

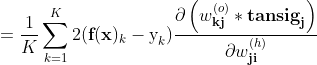
$=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \left ( w_\textbf{kj}^{(o)}*\textbf{tansig}_\textbf{j} \right ) }{\partial w_\textbf{ji}^{(h)}}$

继续求导
$\displaystyle \begin{aligned} &=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})\dfrac{\partial \left ( w_\textbf{kj}^{(o)}*\textbf{tansig}_\textbf{j} \right ) }{\partial w_\textbf{ji}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left ( \textbf{tansig}_\textbf{j} \right ) }{\partial w_\textbf{ji}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial w_\textbf{ji}^{(h)}} \end{aligned}$ $\color{blue}=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }\dfrac{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }{\partial w_\textbf{ji}^{(h)}}$ $\displaystyle \begin{aligned} &=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }x_\textbf{i} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)}) \right ) }{\partial (\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)})}x_\textbf{i} \end{aligned}$

又由 $\textbf{tansig}'(x) = 1-\textbf{tansig}^2(x)$
所以上式为：
$\dfrac{\partial \textbf{E}_m }{\partial w_\textbf{ji}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}* \left (1-\textbf{tansig}_\textbf{j}^2\right ) x_\textbf{i}$
简写为
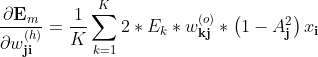
$\displaystyle \dfrac{\partial \textbf{E}_m }{\partial w_\textbf{ji}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *E_k*w_\textbf{kj}^{(o)}* \left (1-A_\textbf{j}^2\right ) x_\textbf{i}$

上述是单样本的梯度，对整体样本则有：
$\displaystyle \dfrac{\partial \textbf{E} }{\partial w_\textbf{ji}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right ) x_\textbf{im}$
M,KM,K为样本个数、输出个数
$E_\textbf{km}=\textbf{f}(\textbf{x})_\textbf{km}-\text{y}_\textbf{km}$ 是第m个样本第k个输出的误差
$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值
$x_\textbf{im}$ 是第m个样本第i个输入

3.5 隐层阈值的梯度推导

隐层阈值梯度推导
对于阈值b_\textbf{j}^{(h)} (第j个隐节点的阈值)的推导与隐层权重梯度的推导是类似的，
只是蓝色部分应改为

$\displaystyle \begin{aligned} &=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) \right ) }{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }\dfrac{\partial (w_\textbf{j1}^{(h)}x_\textbf{1}+...+w_\textbf{ji}^{(h)}x_\textbf{i}+...+w_\textbf{jn}^{(h)}x_\textbf{n}+b_\textbf{j}^{(h)}) }{\partial b_\textbf{j}^{(h)}} \\&=\dfrac{1}{K} \sum \limits _{k=1}^{K}2 (\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}*\dfrac{\partial \left (\textbf{tansig}(\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)}) \right ) }{\partial (\textbf{w}_\textbf{j:}^{(h)}\textbf{x}+b_\textbf{j}^{(h)}) } \end{aligned}$

又由 $\textbf{tansig}'(x) = 1-\textbf{tansig}^2(x)$
所以上式为：
$\dfrac{\partial \textbf{E}_m }{\partial b_\textbf{j}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *(\textbf{f}(\textbf{x})_{k}-\text{y}_{k})*w_\textbf{kj}^{(o)}* \left (1-\textbf{tansig}_\textbf{j}^2\right )$
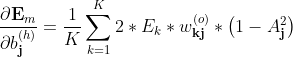
简写为 $\displaystyle \dfrac{\partial \textbf{E}_m }{\partial b_\textbf{j}^{(h)}} =\dfrac{1}{K} \sum \limits _{k=1}^{K}2 *E_k*w_\textbf{kj}^{(o)}* \left (1-A_\textbf{j}^2\right )$

上述是单样本的梯度，对整体样本则有：
$\displaystyle \dfrac{\partial \textbf{E} }{\partial b_\textbf{j}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right )$
M,K为样本个数、输出个数
$E_\textbf{km}=\textbf{f}(\textbf{x})_\textbf{km}-\text{y}_\textbf{km}$ 是第m个样本第k个输出的误差
$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值

四. 推导结果总结

4.1 三层BP神经网络梯度公式

输出层梯度公式
输出层权重梯度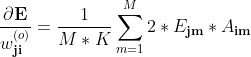： $\displaystyle \dfrac{\partial \textbf{E}}{w_\textbf{ji}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} 2 *E_\textbf{jm}*A_\textbf{im}$
输出层阈值梯度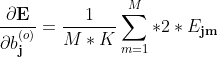： $\displaystyle \dfrac{\partial \textbf{E}}{\partial b_\textbf{j}^{(o)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M}* 2 *E_\textbf{jm}$

隐层梯度公式
隐层权重梯度： $\displaystyle \dfrac{\partial \textbf{E} }{\partial w_\textbf{ji}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right ) x_\textbf{im}$
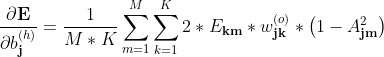
隐层阈值梯度： $\displaystyle \dfrac{\partial \textbf{E} }{\partial b_\textbf{j}^{(h)}} = \dfrac{1}{M*K}\sum\limits_{m=1}^{M} \sum \limits _{k=1}^{K}2 *E_\textbf{km}*w_\textbf{jk}^{(o)}* \left (1-A_\textbf{jm}^2\right )$

✍️符号说明
M,K为样本个数、输出个数
$E_\textbf{km}=\textbf{f}(\textbf{x})_\textbf{km}-\text{y}_\textbf{km}$ 是第m个样本第k个输出的误差
$A_\textbf{im}=\textbf{tansig}_\textbf{im}$ 是第m个样本第i个隐节点的激活值
$x_\textbf{im}$ 是第m个样本第i个输入

相关文章

《BP神经网络梯度推导》

《BP神经网络提取的数学表达式》

《一个BP的完整建模流程》

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：程序员都在用的免费常用API

下一篇：Python 模块和包

BP神经网络的梯度公式推导(三层结构)

一. 推导目标

1.1 梯度公式目标

1.2 本文梯度公式目标

二. 网络表达式梳理

2.1 梳理三层BP神经网络的网络表达式

三. 三层BP神经网络梯度推导过程

3.1 简化推导目标

3.2 输出层权重的梯度推导

3.3 输出层阈值的梯度推导

3.4隐层权重的梯度推导

3.5 隐层阈值的梯度推导

四. 推导结果总结

4.1 三层BP神经网络梯度公式

相关内容

热门资讯