《图机器学习》-GNN Augmentation and Training
创始人
2024-05-27 09:32:44
0次
GNN Augmentation and Training
- 一、Graph Augmentation for GNNs
- 1、Feature Augmentation
- 2、Structure augmentation
- 3、Node Neighborhood Sampling
一、Graph Augmentation for GNNs
之前的假设:
Raw input graph = computational graph,即原始图等于计算图。
现在要打破这个假设,原因如下:
- 如果图过于稀疏:消息传递效率低下
- 如果图过于密集了:消息传递的开销太大
- 如要点击查看某个名人的embedding,要汇聚其成千上万个追随者的信息,这个花销是很大的
- 如果图很大:难以将计算图拟合到CPU内存中
所以,原始输入图不太可能恰好是嵌入的最佳计算图。因此需要Graph Augmentation,改变解构使之适于嵌入。
1、Feature Augmentation
为什么我们需要特征增强?
(1)、输入图没有节点特征;如只有邻接矩阵的时候。
解决方案:
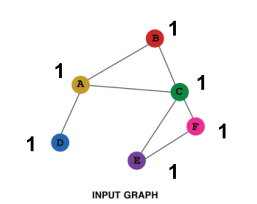
- 为节点分配常量值
如为每个节点都分配一个常数1,在一轮汇聚后,各节点就能学习到其邻居节点的个数。
- 为节点分配唯一的IDs
如为每个节点都分配one-hot编码

该方法每个node的向量不一样,增加了模型的表达能力,但是花费的代价非常大,如one-hot编码的维度和节点数量一致
两种方式的对比:
| Constant node feature | One-hot node feature | |
|---|---|---|
| 表达能力 | 中等。所有的节点都是相同的,但GNN仍然可以从图结构中学习 | 高。每个节点都有唯一的ID,因此可以存储特定于节点的信息 |
| 归纳学习(推广到新的节点) | 高。推广到新节点很简单:我们为它们分配恒定的特征,然后应用我们的GNN | 低。不能泛化到新节点:新节点引入新ID, GNN不知道如何嵌入看不见的ID |
| 计算成本 | 低。只有一维特征 | 高。O(|V|)维度特征,不能应用于大型图 |
| 使用范围 | 任何图 | 小图 |
为什么我们需要特征增强?
(2)、GNN很难学习某些结构
如:计算节点所处环的节点数
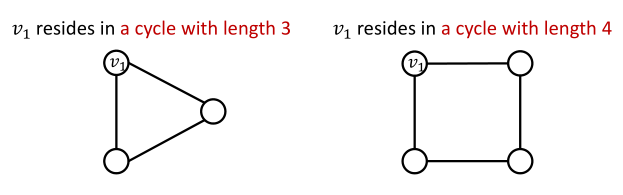
基于前面的GNN是不能够解答这个问题的,原因是这两个节点的计算图是一样的,学习出来的embedding大致类似
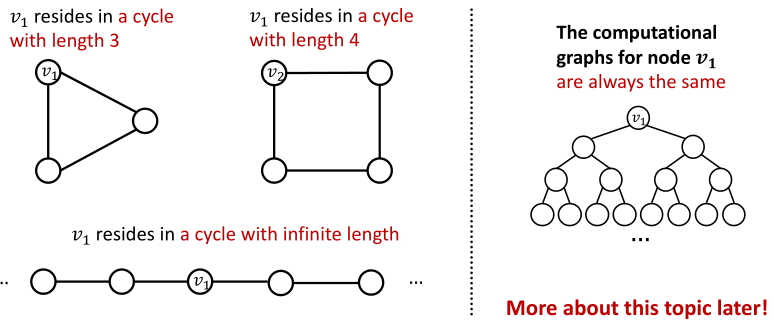
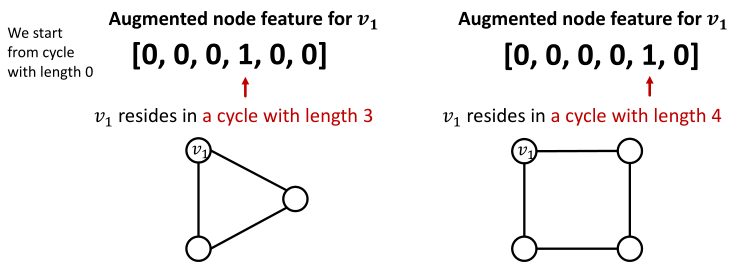
解决方案:
可以添加cycle count作为节点的特征,如下图;即开辟一个特征空间用于描述所需要的属性。
其他常用于数据增强的特征:
- Node degree
- Clustering coefficient
- PageRank
- Centrality
2、Structure augmentation
出发点: Augment sparse graphs(增强稀疏图)
-
Add virtual edges
- 常见的方法:通过虚边连接2跳邻居
- 如:将邻接矩阵AAA使用A+A2A+A^2A+A2代替
- 实例:Bipartite graphs。
使用2-hop的虚边将作者节点连接起来

-
Add virtual nodes
增加一个虚拟节点,虚拟节点将于图中的所有节点相连接- 好处:
- 缩短节点之间的距离(均可两跳可达)
- 传递信息更多、更有效、更快
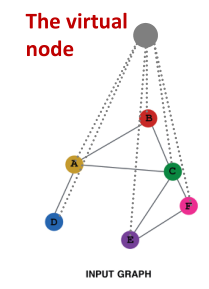
- 好处:
3、Node Neighborhood Sampling
回顾之前的GNN计算图,所有节点都用于消息传递,如下图:
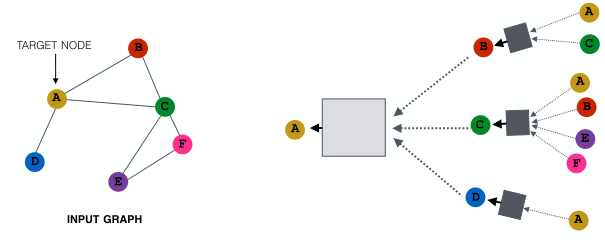
新的想法:
随机的选取邻居节点的子集用于计算图的构建(用于信息传递)
例如,可以在给定的层中随机选择2个邻居来传递消息,如下图:
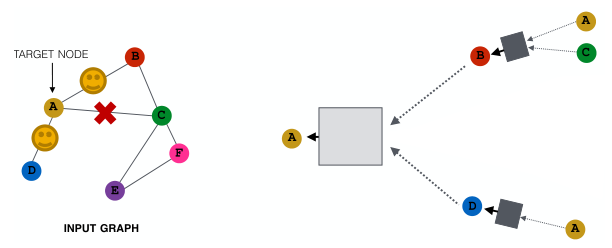
在大图中,随机采样邻居节点的子集用于信息传递能够减少计算图;但会丢失信息,即获得了效率但失去了一些表现力。
为了弥补,可以在下一层中,当我们计算嵌入时,对不同的邻居进行采样(即每一层都采样不同的邻居用于计算图的构建),提升模型的鲁棒性。
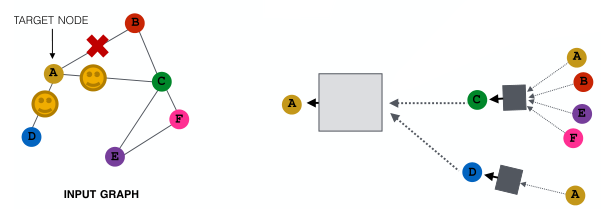
该方法在实践中效果不错。
相关内容
热门资讯
安卓9系统怎样应用分身,轻松实...
你有没有发现,手机里的APP越来越多,有时候一个APP里还要处理好多任务,分身功能简直就是救星啊!今...
获取安卓系统的ip地址,轻松获...
你有没有想过,你的安卓手机里隐藏着一个神秘的IP地址?没错,就是那个能让你在网络世界里找到自己的小秘...
LG彩电安卓系统升级,畅享智能...
你家的LG彩电是不是最近有点儿“闹别扭”,屏幕上时不时地跳出个升级提示?别急,今天就来给你详细说说这...
阴阳师安卓苹果系统,安卓与苹果...
亲爱的玩家们,你是否曾在深夜里,手握手机,沉浸在阴阳师的神秘世界?今天,就让我带你一起探索这款风靡全...
华为安卓系统区别在哪,独特创新...
你知道吗?最近手机圈里可是热闹非凡,尤其是华为的新动作,让很多人眼睛都瞪大了。没错,我说的就是华为自...
怎么重新刷安卓手机系统,深度解...
手机用久了,是不是感觉卡顿得厉害?别急,今天就来教你怎么重新刷安卓手机系统,让你的手机焕然一新,速度...
刷正版安卓系统教程,刷正版安卓...
你有没有想过,让你的安卓手机焕然一新,体验一把正版系统的魅力呢?别急,今天就来手把手教你如何刷正版安...
移动支撑系统安卓版,助力移动办...
你有没有发现,现在的生活越来越离不开手机了?无论是工作还是娱乐,手机几乎成了我们生活的必需品。而今天...
安卓怎么进win系统界面,安卓...
亲爱的安卓用户,你是否曾幻想过在安卓设备上直接体验Windows系统的魅力?别再羡慕那些Window...
incall可以升级安卓系统吗...
你有没有想过,你的手机是不是也能像电脑一样,时不时地来个系统升级呢?今天,咱们就来聊聊这个话题——i...
安卓系统带农历软件,尽享传统节...
你知道吗?现在智能手机上有个特别实用的功能,那就是农历显示。对于咱们中国人来说,农历可是有着深厚的历...
安卓系统资源占用高,揭秘原因与...
你有没有发现,你的安卓手机最近变得越来越慢了?是不是觉得打开一个应用都要等半天,甚至有时候还会卡死?...
安卓10的系统有哪些,功能升级...
你有没有发现,你的安卓手机最近是不是变得有点不一样了?没错,就是那个神秘的安卓10系统!它就像一位魔...
固态硬盘系统迁移到安卓,固态硬...
你有没有想过,把你的固态硬盘系统迁移到安卓设备上,是不是能让你在移动办公或者娱乐时更加得心应手呢?想...
平板电脑能玩安卓系统吗,畅享丰...
你有没有想过,平板电脑竟然也能玩安卓系统?这可不是天方夜谭,而是科技发展的新趋势。想象你手中的平板瞬...
安卓刷精简系统下载,轻松打造高...
你有没有想过,你的安卓手机是不是有点儿“臃肿”了呢?运行速度慢,电池续航短,有时候还卡得要命。别急,...
安卓子系统windows11,...
你知道吗?最近科技圈可是炸开了锅,因为安卓子系统在Windows 11上的兼容性成了大家热议的话题。...
电脑里怎么下载安卓系统,电脑端...
你有没有想过,你的电脑里也能装上安卓系统呢?没错,就是那个让你手机不离手的安卓!今天,就让我来带你一...
索尼相机魔改安卓系统,魔改系统...
你知道吗?最近在摄影圈里掀起了一股热潮,那就是索尼相机魔改安卓系统。这可不是一般的改装,而是让这些专...
安卓系统哪家的最流畅,安卓系统...
你有没有想过,为什么你的手机有时候像蜗牛一样慢吞吞的,而别人的手机却能像风一样快?这背后,其实就是安...
