二叉搜索树中的插入操作

链接
给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

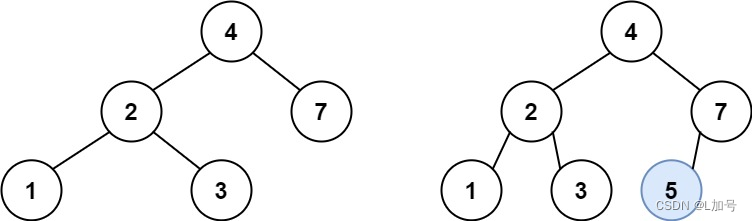
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：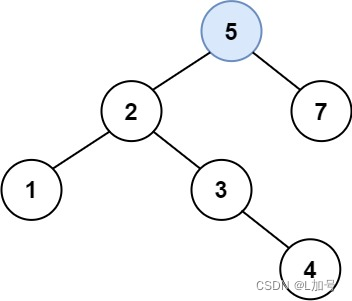

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]
示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。

思路

搜索树插入，永远都是插到空节点处，不可能拆掉已有节点换上，比当前节点小就放左边，大就放右边，递归下去

• 终止条件
  到了空节点处，插入这里

        if(root==NULL) {TreeNode* node=new TreeNode(val);return node;}

这里是root比目标值小，插入右边子树

        if(root->valTreeNode* right=insertIntoBST(root->right,val);root->right=right;}

class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==NULL) {TreeNode* node=new TreeNode(val);return node;}if(root->valTreeNode* right=insertIntoBST(root->right,val);root->right=right;}if(root->val>val){TreeNode* left=insertIntoBST(root->left,val);root->left=left;}return root;}
};

代改进点

        if(root->valTreeNode* right=insertIntoBST(root->right,val);root->right=right;}

把插入放入递归函数下面，造成每次递归回调后都会进行一次插入
第一次是将插入值5插入，第二次则是返回当前函数节点 7重新成为节点 4 的右节点（7本来就是4的右节点，重复操作）
除了第一次插入操作有效，其他插入操作为冗余操作