CEC2020:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2020(提供MATLAB代码
一、鱼鹰优化算法简介
鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovský于2023年提出,其模拟鱼鹰的捕食行为。

鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米,体重1000-1750克。头部白色,头顶具有黑褐色的纵纹,枕部的羽毛稍微呈披针形延长,形成一个短的羽冠。头的侧面有一条宽阔的黑带,从前额的基部经过眼睛到后颈部,并与后颈的黑色融为一体。上体为暗褐色,略微具有紫色的光泽。下体为白色,胸部的暗色纵纹和飞羽,以及尾羽上相间排列的横斑均极为醒目。虹膜淡黄色或橙黄色,眼周裸露皮肤铅黄绿色,嘴黑色,蜡膜铅蓝色,脚和趾黄色,爪黑色。
鱼鹰栖息于湖泊、河流、海岸或开阔地,尤其喜欢在山地森林中的河谷或有树木的水域地带活动。常见在江河、湖沼及海滨一带飞翔,一见水中有饵,就直下水面,用脚掠之而去。趾具锐爪,趾底遍生细刺,外趾复能由前向后反转,这些都很适于捕鱼。在天气晴朗之日,盘旋于水面上空,定点后俯冲而下,再将捕获的鱼带至岩石、电杆、树上等地方享用。巢常营于海岸或岛屿的岩礁上。主要以鱼为食,有时也捕食蛙、蜥蜴、小型鸟类等其他小型陆栖动物。除了南极和北极,亚洲、北美洲等各大洲均有分布。
1.1鱼鹰优化算法原理
鱼鹰优化算法包含两个阶段:第一阶段为鱼鹰识别鱼的位置并捕鱼(全局勘探), 第二阶段为将鱼带到合适的位置( 局部开采),其详细设计如下:
1.1.1 种群初始化
采用下式随机初始化鱼鹰种群:
X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,j⋯x1,m⋮⋱⋮⋱⋮xi,1⋯xi,j⋯xi,m⋮⋱⋮⋱⋮xN,1⋯xN,j⋯xN,m]N×m,xi,j=lbj+ri,j⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,\begin{array}{c} X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m}, \\ x_{i, j}=l b_{j}+r_{i, j} \cdot\left(u b_{j}-l b_{j}\right), i=1,2, \ldots, N, j=1,2, \ldots, m, \end{array}X=X1⋮Xi⋮XNN×m=x1,1⋮xi,1⋮xN,1⋯⋱⋯⋱⋯x1,j⋮xi,j⋮xN,j⋯⋱⋯⋱⋯x1,m⋮xi,m⋮xN,mN×m,xi,j=lbj+ri,j⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,
其中,N为鱼鹰的数量,m为问题的维度,初始化位置后依据优化问题计算适应度值:
F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1}F=F1⋮Fi⋮FNN×1=F(X1)⋮F(Xi)⋮F(XN)N×1
1.1.2 全局勘探(第一阶段:位置识别和捕鱼)
鱼鹰是强大的猎人,由于其强大的视力,能够探测到水下鱼类的位置。在确定鱼的位置后,他们攻击它并通过潜入水下捕猎鱼。OOA中种群更新的第一阶段是基于对鱼鹰这种自然行为的模拟而建模的。对鱼鹰攻击鱼类进行建模会导致鱼鹰在搜索空间中的位置发生显著变化,这增加了OOA在识别最优区域和逃离局部最优方面的探索能力。在OOA设计中,对于每只鱼鹰,搜索空间中具有较好目标函数值的其他鱼鹰的位置被视为水下鱼类。每只鱼鹰的位置使用下式指定。
FPi={Xk∣k∈{1,2,…,N}∧Fk
其中,FPiF P _ { i }FPi为第i只鱼鹰的位置集合,Xbest {X}_{\text {best }}Xbest 为最佳鱼鹰的位置。
鱼鹰随机检测其中一条鱼的位置并攻击它。基于鱼鹰向鱼的运动模拟,使用下式计算相应鱼鹰的新位置。这个新位置,如果它的目标函数的值更好,则替换鱼鹰的先前位置。
xi,jP1=xi,j+ri,j⋅(SFi,j−Ii,j⋅xi,j),xi,jP1={xi,jP1,lbj≤xi,jP1≤ubj;lbj,xi,jP1
1.1.3 局部开采(第二阶段:将鱼带到合适的位置)
捕食鱼后,鱼鹰将其带到合适(对他来说安全)的位置,并在那里吃。OOA中更新种群的第二阶段是基于鱼鹰这种自然行为的模拟建模的。将鱼带到合适位置的建模导致鱼鹰在搜索空间中的位置发生微小变化,从而导致 OOA 在本地搜索中的开发能力增加,并在发现的解决方案附近收敛到更好的解决方案。在OOA的设计中,为了模拟鱼鹰的这种自然行为,首先,针对种群的每个成员,使用下式计算一个新的随机位置作为“适合吃鱼的位置”。然后,如果目标函数的值在这个新位置得到改善,则替换相应鱼鹰的先前位置。
xi,jP2=xi,j+lbj+r⋅(ubj−lbj)t,i=1,2,…,N,j=1,2,…,m,t=1,2,…,T,xi,jP2={xi,jP2,lbj≤xi,jP2≤ubj;lbj,xi,jP2
1.2算法描述

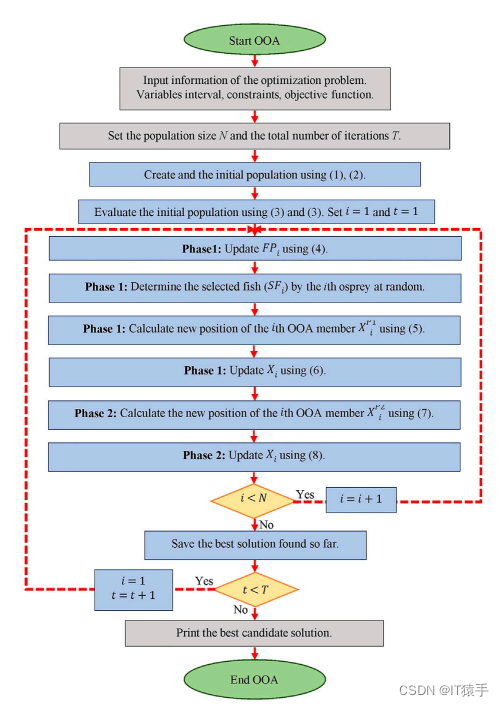
1.3算法流程
1.4参考文献
Dehghani Mohammad, Trojovský Pavel.Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems[J].Frontiers in Mechanical Engineering,2023,8.
二、CEC2020简介
CEC2020共有10个测试函数测试维度包含:2D、5D、10D、15D、20D。CEC2020测试问题随着维度的增加求解极其困难。

三、求解结果
完整代码添加博客下方博主微信:djpcNLP123
将鱼鹰优化算法OOA运用于求解CEC2020中10个函数,其中每个测试函数可以选择的维度分别有:2D、5D、10D、15D、20D。增大迭代次数,鱼鹰优化算法OOA的求解效果更佳。本例测试函数维度均为10D(可根据自己需求调整),种群大小为50,最大迭代次数为100次。
close all
clear
clc
MaxFes = 50;%迭代次数
VarNumber = 10;%维度 2/5/10/15/20
nPop = 50;%种群大小
VarMin=-100;%下限
VarMax=100;%上限
fitnessfunc=str2func('cec20_func');
Function_name=1;%测试函数1-10
[Best_Fit,Best_Pos,Curve]=OOA(nPop,MaxFes,VarMin,VarMax,VarNumber,CostFunction);
figure
plot(Curve,'g','linewidth',2.5)
xlabel('迭代次数')
ylabel('适应度值')
legend('OOA')
title(strcat('CEC2020-F',num2str(Function_name)))部分求解结果:
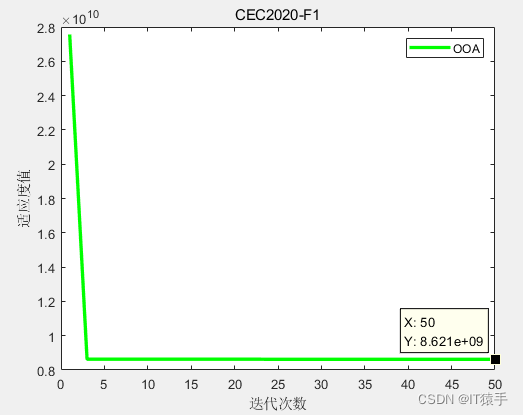
F1:
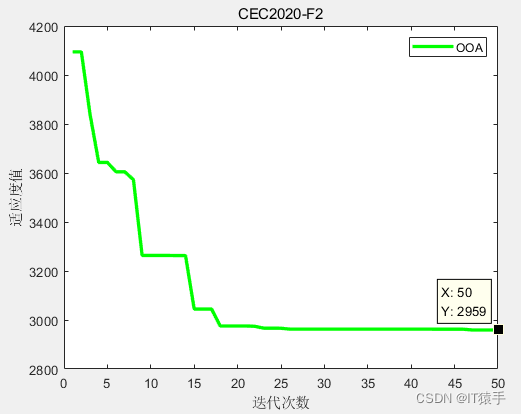
F2:
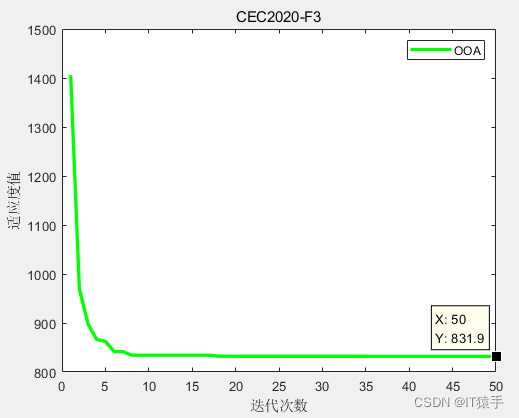
F3:
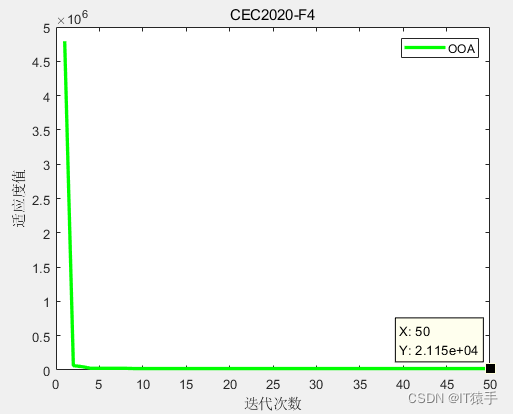
F4:
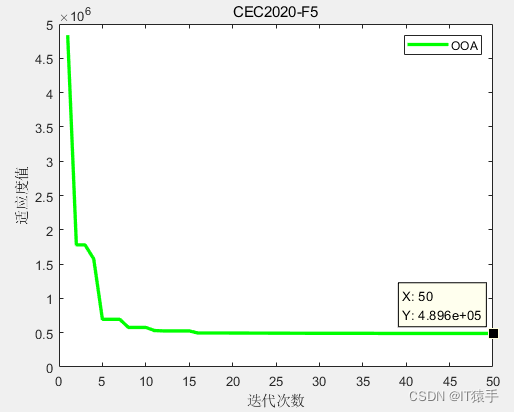
F5:
四、参考代码
完整代码添加博客下方博主微信:djpcNLP123
下一篇:《SQL基础》15. 触发器
