本系列基本不讲数学原理，只从代码角度去让读者们利用最简洁的Python代码实现机器学习方法。

背景：

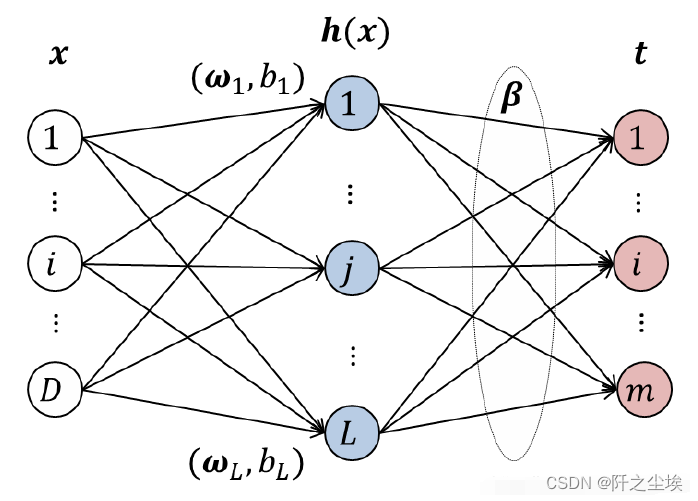
极限学习机(ELM)也是学术界常用的一种机器学习算法，严格来说它应该属于神经网络，应该属于深度学习栏目，但是我这里把它放在了机器学习栏目里面，主要还是这个方法不是像别的神经网络一样方向传播误差去更新参数的。他是一个静态的模型 ，虽然它结构类似于多层感知机，只不过多层感知机的参数会随着迭代次数增加通过方向传播误差进行更新，而ELM不会，所以ELM的效果肯定是不如MLP的。

但是我也不知道为什么效果不好的模型学术界这么喜欢用......一堆论文不用MLP而是去用ELM....可能因为它不需要深度学习框架就可以搭建，而且运行速度快吧，门槛低，可能是不懂深度学习的人接触的最简单的神经网络实现的方法了。

sklearn库没有现成的接口调用，我们下面的ELM都是自定义的类，模仿sklearn的接口使用。

当然单纯的ELM由于它的权重矩阵都是静态的，效果不好，所以可以使用拟牛顿法或者别的梯度下降的方法根据误差去优化其参数矩阵，达到更好的效果。（说实话这不就是MLP嘛....）

下面会自定义ELM和优化的ELM两个类，还给出了一个基于优化的ELM结合ER回归的类。

（请注意我这里都是回归问题的ELM代码，分类问题还需要进行改动）

代码实现

原理就不多介绍了，别的文章都有，我直接给ELM的代码案例。本次使用一个回归问题，16的特征变量，响应变量是一个数值，使用ELM预测。

导入包，然后读取数据，取出X和y，我数据的最后一列就是y，然后给它划分训练集和测试集。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
plt.rcParams ['font.sans-serif'] ='SimHei'               #显示中文
plt.rcParams ['axes.unicode_minus']=False               #显示负号# 加载数据
data =pd.read_csv('CS2_35的特征.csv')
X = data.iloc[:,:-1]
y = data.iloc[:,-1]# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

标准化一下：

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_s = scaler.transform(X_train)
X_test_s = scaler.transform(X_test)
print('训练数据形状：')
print(X_train_s.shape,y_train.shape)
print('测试数据形状：')
print(X_test_s.shape,y_test.shape)

自定义ELM类 

class ELMRegressor():def __init__(self, n_hidden):self.n_hidden = n_hiddendef fit(self, X, y):self.X = Xself.y = yn_samples, n_features = X.shapeself.W = np.random.randn(n_features+1, self.n_hidden)H = np.dot(np.concatenate((X, np.ones((n_samples, 1))), axis=1), self.W)H = np.maximum(H, 0)self.beta = np.dot(np.linalg.pinv(H), y)def predict(self, X):n_samples = X.shape[0]H = np.dot(np.concatenate((X, np.ones((n_samples, 1))), axis=1), self.W)H = np.maximum(H, 0)y_pred = np.dot(H, self.beta)return y_pred

自定义优化参数矩阵的ELM类

这里采用scipy.optimize 里面的minimize方法，使用拟牛顿法进行优化参数矩阵。

from scipy.optimize import minimize
class OP_ELMRegressor():def __init__(self, n_hidden):self.n_hidden = n_hiddendef fit(self, X, y):self.X = Xself.y = yn_samples, n_features = X.shapeself.W = np.random.randn(n_features + 1, self.n_hidden)def loss_func(W_vec):W = W_vec.reshape((n_features + 1, self.n_hidden))H = np.dot(np.hstack((X, np.ones((n_samples, 1)))), W)H = np.maximum(H, 0)beta = np.dot(np.linalg.pinv(H), y)y_pred = np.dot(H, beta)mse = np.mean((y - y_pred) ** 2)return mse# 用拟牛顿法优化权重矩阵res = minimize(loss_func, self.W.ravel(), method='BFGS')self.W = res.x.reshape((n_features + 1, self.n_hidden))H = np.hstack((X, np.ones((n_samples, 1))))  # 添加偏置项H = np.dot(H, self.W)H = np.maximum(H, 0)self.beta = np.dot(np.linalg.pinv(H), y)def predict(self, X):n_samples = X.shape[0]H = np.hstack((X, np.ones((n_samples, 1))))H = np.dot(H, self.W)H = np.maximum(H, 0)y_pred = np.dot(H, self.beta)return y_pred

自定义优化参数矩阵的ELM结合ER回归的类

不懂什么是ER回归可以去搜一下....核心改动就是损失函数改了，不是MSE损失，而是ER损失。总之这是一种机器学习结合统计学的方法，算得上创新。

class OP_ELMRegressor_ER():def __init__(self, n_hidden,tau):self.n_hidden = n_hiddenself.tau = taudef fit(self, X, y):self.X = Xself.y = yn_samples, n_features = X.shapeself.W = np.random.randn(n_features + 1, self.n_hidden)def loss_func(W,tau=self.tau):W = W.reshape((n_features + 1, self.n_hidden))H = np.dot(np.hstack((X, np.ones((n_samples, 1)))), W)H = np.maximum(H, 0)beta = np.dot(np.linalg.pinv(H), y)y_pred = np.dot(H, beta)loss=np.mean(np.where(np.greater(y,y_pred),np.power((y-y_pred),2)*tau,np.power((y-y_pred),2)*(1-tau)))return loss# 用拟牛顿法优化权重矩阵res = minimize(loss_func, self.W.ravel(), method='BFGS')self.W = res.x.reshape((n_features + 1, self.n_hidden))H = np.hstack((X, np.ones((n_samples, 1))))  # 添加偏置项H = np.dot(H, self.W)H = np.maximum(H, 0)self.beta = np.dot(np.linalg.pinv(H), y)def predict(self, X):n_samples = X.shape[0]H = np.hstack((X, np.ones((n_samples, 1))))H = np.dot(H, self.W)H = np.maximum(H, 0)y_pred = np.dot(H, self.beta)return y_pred

导入别的模型对比

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor

定义评价函数，这里计算MAE,RMSE,MAPE,R2来评价预测效果。

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_scoredef evaluation(y_test, y_predict):mae = mean_absolute_error(y_test, y_predict)mse = mean_squared_error(y_test, y_predict)rmse = np.sqrt(mean_squared_error(y_test, y_predict))mape=(abs(y_predict -y_test)/ y_test).mean()r_2=r2_score(y_test, y_predict)return mae, rmse, mape,r_2  #mse

生成11个模型类的实例化，装入列表。

#线性回归
model1 = LinearRegression()#弹性网回归
model2 = ElasticNet(alpha=0.05, l1_ratio=0.5)#K近邻
model3 = KNeighborsRegressor(n_neighbors=10)#决策树
model4 = DecisionTreeRegressor(random_state=77)#随机森林
model5= RandomForestRegressor(n_estimators=500,  max_features=int(X_train.shape[1]/3) , random_state=0)#梯度提升
model6 = GradientBoostingRegressor(n_estimators=500,random_state=123)#支持向量机
model7 = SVR(kernel="rbf")#神经网络
model8 = MLPRegressor(hidden_layer_sizes=(64,40), random_state=77, max_iter=10000)#MLE
model9=ELMRegressor(32)#优化MLE
model10=OP_ELMRegressor(16)#优化MLE_ER
model11=OP_ELMRegressor_ER(16,tau=0.5)model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10,model11]
model_name=['线性回归','惩罚回归','K近邻','决策树','随机森林','梯度提升','支持向量机','神经网络','极限学习机','优化极限学习机','优化极限学习机+ER']

训练，评价，计算误差指标

df_eval=pd.DataFrame(columns=['MAE','RMSE','MAPE','R2'])
for i in range(len(model_list)):model_C=model_list[i]name=model_name[i]print(f'{name}正在训练...')model_C.fit(X_train_s, y_train)pred=model_C.predict(X_test_s)s=evaluation(y_test,pred)df_eval.loc[name,:]=list(s)

 查看：

df_eval

画图：

bar_width = 0.4
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan','purple']
fig, ax = plt.subplots(2,2,figsize=(7,5),dpi=256)
for i,col in enumerate(df_eval.columns):n=int(str('22')+str(i+1))plt.subplot(n)df_col=df_eval[col]m =np.arange(len(df_col))#hatch=['-','/','+','x'],plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)#plt.xlabel('Methods',fontsize=12)names=df_col.indexplt.xticks(range(len(df_col)),names,fontsize=8)plt.xticks(rotation=40)if col=='R2':plt.ylabel(r'$R^{2}$',fontsize=14)else:plt.ylabel(col,fontsize=14)
plt.tight_layout()
#plt.savefig('柱状图.jpg',dpi=512)
plt.show()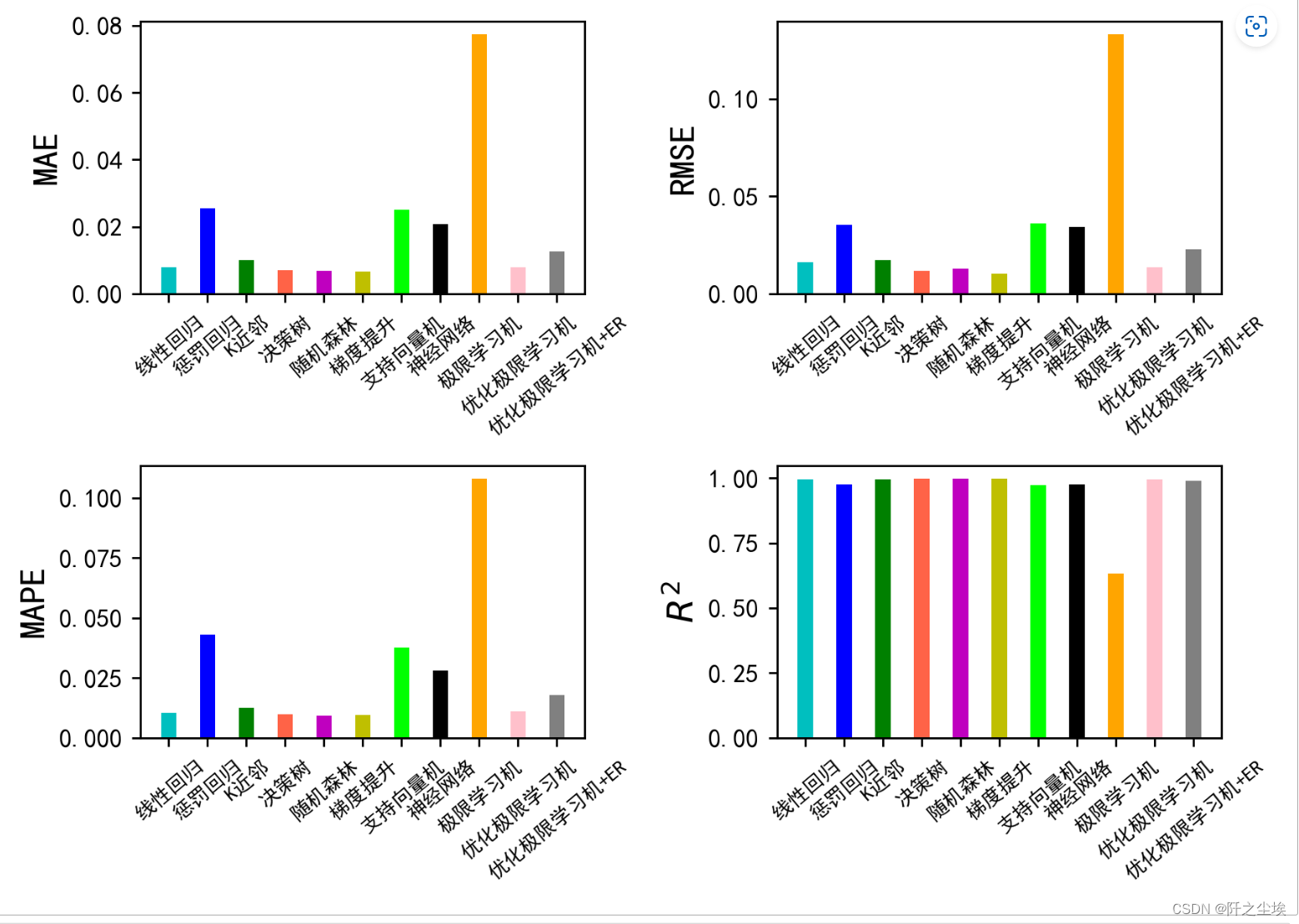

 从效果上来看，这个数据集的X对y的解释能力还是很强的，线性回归的拟合优度都到了99%，所以基本模型都差不多是这个表现。单纯的ELM的表现比线性回归还差，但是用拟牛顿法优化过后效果还不错，加了ER效果也是差不多的。ER还有分位数tau这个参数可以改，说不定能出更好的效果。

整体来说是一个效果一般的机器学习模型，但是原理简单，可以很容易去改动和创新，然后发文章，所以学术界都喜欢用这个吧。。。