文章目录

• 导数与微分
• • 概念
  • 几何意义
  • 连续、可导、可微之间的关系
  • 求导法则
  • • 基本初等函数的导数公式
    • 有理运算法则
    • 复合函数求导法
    • 奇偶性和周期性
    • 隐函数求导
    • 反函数求导
    • 参数方程求导
    • 对数求导法
  • 高阶导数
  • • 概念
    • 常用的高阶导数公式
• 微分中值定理和导数的应用
• • 微分中值定理
  • 导数的应用
  • • 函数的单调性
    • 函数的极值
    • 函数的最大值和最小值
    • 曲线的凹凸性
    • 曲线的渐近线
    • 曲线的弧微分和曲率

导数与微分

导数用来研究函数在某一点的变化率。微分用来表示函数改变量的近似值。

概念

• 导数：设函数y=f(x)y=f(x)y=f(x)在x0x_0x0​的某邻域内有定义，如果极限lim⁡x→x0ΔyΔx=lim⁡Δx→0f(x0+Δx)−f(x0)Δx=lim⁡x→x0f(x)−f(x0)x−x0\lim\limits_{x\to x_0}\frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}x→x0​lim​ΔxΔy​=Δx→0lim​Δxf(x0​+Δx)−f(x0​)​=x→x0​lim​x−x0​f(x)−f(x0​)​存在，则称f(x)f(x)f(x)在点x0x_0x0​处可导，并称此极限值为f(x)f(x)f(x)在点x0x_0x0​处的导数，记为f′(x0)f'(x_0)f′(x0​)或y′∣x=x0y'|_{x=x_0}y′∣x=x0​​或dydx∣x=x0\frac{dy}{dx}|_{x=x_0}dxdy​∣x=x0​​。如果上述极限不存在，则称f(x)f(x)f(x)在点x0x_0x0​处不可导。

• 左导数：设函数y=f(x)y=f(x)y=f(x)在x0x_0x0​及其某个左邻域内有定义，如果左极限lim⁡Δx→0−ΔyΔx=lim⁡Δx→0−f(x0+Δx)−f(x0)Δx=lim⁡x→x0−f(x)−f(x0)x−x0\lim\limits_{\Delta x\to 0^-}\frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\to 0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim\limits_{x\to x_0^-}\frac{f(x)-f(x_0)}{x-x_0}Δx→0−lim​ΔxΔy​=Δx→0−lim​Δxf(x0​+Δx)−f(x0​)​=x→x0−​lim​x−x0​f(x)−f(x0​)​存在，则称此极限值为f(x)f(x)f(x)在点x0x_0x0​处的左导数，记为f−′(x0)f'_-(x_0)f−′​(x0​)。

• 右导数：设函数y=f(x)y=f(x)y=f(x)在x0x_0x0​及其某个右邻域内有定义，如果右极限lim⁡Δx→0+ΔyΔx=lim⁡Δx→0+f(x0+Δx)−f(x0)Δx=lim⁡x→x0+f(x)−f(x0)x−x0\lim\limits_{\Delta x\to 0^+}\frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\to 0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim\limits_{x\to x_0^+}\frac{f(x)-f(x_0)}{x-x_0}Δx→0+lim​ΔxΔy​=Δx→0+lim​Δxf(x0​+Δx)−f(x0​)​=x→x0+​lim​x−x0​f(x)−f(x0​)​存在，则称此极限值为f(x)f(x)f(x)在点x0x_0x0​处的右导数，记为f+′(x0)f'_+(x_0)f+′​(x0​)。

• 函数f(x)f(x)f(x)在点x0x_0x0​处可导的充要条件：f(x)f(x)f(x)在点x0x_0x0​处的左导数和右导数都存在且相等。

• 区间可导：若f(x)f(x)f(x)在区间(a，b)(a，b)(a，b)内每点都可导，则称f(x)f(x)f(x)在区间(a,b)(a,b)(a,b)内可导，如果f(x)f(x)f(x)在x=ax=ax=a处有右导数，在x=bx=bx=b处有左导数，则称f(x)f(x)f(x)在[a,b][a,b][a,b]上可导。

• 导函数：如果f(x)f(x)f(x)在区间(a,b)(a,b)(a,b)内可导，此时对于(a,b)(a,b)(a,b)内的每一点xxx都对应一个导数值f′(x)f'(x)f′(x)，常称f′(x)f'(x)f′(x)为f(x)f(x)f(x)在(a,b)(a,b)(a,b)内的导函数。

• 微分：设函数y=f(x)y=f(x)y=f(x)在x0x_0x0​的某邻域内有定义，如果函数的增量Δy=f(x0+Δx)−f(x0)\Delta y=f(x_0+\Delta x)-f(x_0)Δy=f(x0​+Δx)−f(x0​)可以表示为Δy=AΔx+o(Δx)(Δx→0)\Delta y=A\Delta x+o(\Delta x) (\Delta x\to 0)Δy=AΔx+o(Δx)(Δx→0)其中A为不依赖于Δx\Delta xΔx的常数，则称f(x)f(x)f(x)在点x0x_0x0​处可微，称AΔxA\Delta xAΔx为函数f(x)f(x)f(x)在点x0x_0x0​处相应于自变增量Δx\Delta xΔx的微分，记为dy=AΔxdy=A\Delta xdy=AΔx。函数y=f(x)y=f(x)y=f(x)在x0x_0x0​处可微的充要条件是f(x)f(x)f(x)在点x0x_0x0​处可导，且有dy=f′(x0)Δx=f′(x0)dxdy=f'(x_0)\Delta x=f'(x_0)dxdy=f′(x0​)Δx=f′(x0​)dx在点xxx处，长记dy=f′(x)dxdy=f'(x)dxdy=f′(x)dx。

几何意义

• 导数的几何意义：导数f′(x)f'(x)f′(x)在几何上表示曲线y=f(x)y=f(x)y=f(x)在点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))处切线的斜率，如果函数y=f(x)y=f(x)y=f(x)在x0x_0x0​处可导，则曲线y=f(x)y=f(x)y=f(x)在点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))处必有切线，其切线方程为y−f(x0)=f′(x0)(x−x0)y-f(x_0)=f'(x_0)(x-x_0)y−f(x0​)=f′(x0​)(x−x0​)如果f′(x0)≠0f'(x_0)≠0f′(x0​)=0，则曲线y=f(x)y=f(x)y=f(x)在点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))处的法线方程为y−f(x0)=−1f′(x0)(x−x0)y-f(x_0)=-\frac{1}{f'(x_0)}(x-x_0)y−f(x0​)=−f′(x0​)1​(x−x0​)如果f′(x0)=0f'(x_0)=0f′(x0​)=0，则曲线y=f(x)y=f(x)y=f(x)在点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))处的切线方程为y=f(x0)y=f(x_0)y=f(x0​)即曲线在点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))处有水平切线。
• 微分的几何意义：微分dy=f′(x0)dxdy=f'(x_0)dxdy=f′(x0​)dx在几何上表示曲线y=f(x)y=f(x)y=f(x)的切线上的增量，Δy=f(x0+Δx)−f(x0)\Delta y=f(x_0+\Delta x)-f(x_0)Δy=f(x0​+Δx)−f(x0​)在几何上表示曲线y=f(x)y=f(x)y=f(x)上的增量，当Δx→0\Delta x\to0Δx→0时，Δy≈dy\Delta y≈dyΔy≈dy。

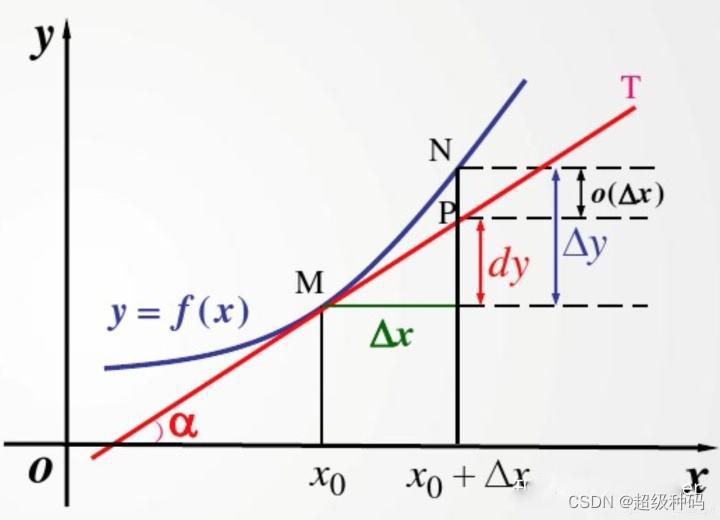
连续、可导、可微之间的关系

• 连续不一定可导，可导一定连续；
• 连续不一定可微，可微一定连续；
• 可导一定可微，可微一定可导；

求导法则

基本初等函数的导数公式

• (C)′=0(C)'=0(C)′=0
• (xa)′=axa−1(x^a)'=ax^{a-1}(xa)′=axa−1
• (ax)′=axlna(a^x)'=a^xlna(ax)′=axlna
• (ex)′=ex(e^x)'=e^x(ex)′=ex
• (logax)′=1xlna(log_ax)'=\frac{1}{xlna}(loga​x)′=xlna1​
• (lnx)′=1x(lnx)'=\frac{1}{x}(lnx)′=x1​
• (sinx)′=cosx(sinx)'=cosx(sinx)′=cosx
• (cosx)′=−sinx(cosx)'=-sinx(cosx)′=−sinx
• (tanx)′=sec2x(tanx)'=sec^2x(tanx)′=sec2x
• (cotx)′=−csc2x(cotx)'=-csc^2x(cotx)′=−csc2x
• (secx)′=secxtanx(secx)'=secxtanx(secx)′=secxtanx
• (cscx)′=−cscxcotx(cscx)'=-cscxcotx(cscx)′=−cscxcotx
• (arcsinx)′=11−x2(arcsinx)'=\frac{1}{\sqrt{1-x^2}}(arcsinx)′=1−x2​1​
• (arccosx)′=−11−x2(arccosx)'=-\frac{1}{\sqrt{1-x^2}}(arccosx)′=−1−x2​1​
• (arctanx)′=11+x2(arctanx)'=\frac{1}{1+x^2}(arctanx)′=1+x21​
• (arccotx)′=−11+x2(arccotx)'=-\frac{1}{1+x^2}(arccotx)′=−1+x21​

有理运算法则

• (u±v)′=u′±v′(u\pm v)'=u'\pm v'(u±v)′=u′±v′
• (uv)′=u′v+uv′(uv)'=u'v+uv'(uv)′=u′v+uv′
• (uv)′=u′v−uv′v′(v≠0)(\frac{u}{v})'=\frac{u'v-uv'}{v'}(v≠0)(vu​)′=v′u′v−uv′​(v=0)

复合函数求导法

设u=φ(x),y=f(u)u=\varphi(x),y=f(u)u=φ(x),y=f(u)可导，则y=f[φ(x)]y=f[\varphi(x)]y=f[φ(x)]在x处可导，且dydx=dydu×dudx=f′(u)φ′(x)\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}=f'(u)\varphi'(x)dxdy​=dudy​×dxdu​=f′(u)φ′(x)。

奇偶性和周期性

• 若f(x)是奇函数，则f′(x)是偶函数若f(x)是奇函数，则f'(x)是偶函数若f(x)是奇函数，则f′(x)是偶函数
• 若f(x)是偶函数，则f′(x)是奇函数若f(x)是偶函数，则f'(x)是奇函数若f(x)是偶函数，则f′(x)是奇函数
• 若f(x)是周期函数，则f′(x)是周期函数若f(x)是周期函数，则f'(x)是周期函数若f(x)是周期函数，则f′(x)是周期函数

隐函数求导

设y=f(x)y=f(x)y=f(x)是由方程F(x,y)=0F(x,y)=0F(x,y)=0所确定的可导函数，为求得y′y'y′，可在方程F(x,y)=0F(x,y)=0F(x,y)=0两边对x求导，可以得到一个含有y′y'y′的方程，解出y′y'y′即可。

反函数求导

若y=f(x)y=f(x)y=f(x)在某区间内可导，且f′(x)≠0f'(x)≠0f′(x)=0，则其反函数x=φ(y)x=\varphi(y)x=φ(y)在对应区间内也可导，且φ′(y)=1f′(x)\varphi'(y)=\frac{1}{f'(x)}φ′(y)=f′(x)1​，即dxdy=1dydx\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}dydx​=dxdy​1​。

参数方程求导

设y=f(x)y=f(x)y=f(x)是由参方程{x=φ(x),y=ψ(x)(αx=φ(x),y=ψ(x)​(α

• 若φ(x)\varphi(x)φ(x)和ψ(x)\psi(x)ψ(x)都可导，且φ′(x)≠0\varphi'(x)≠0φ′(x)=0，则dydx=φ′(t)ϕ′(t)\frac{dy}{dx}=\frac{\varphi'(t)}{\phi'(t)}dxdy​=ϕ′(t)φ′(t)​。
• 若φ(x)\varphi(x)φ(x)和ψ(x)\psi(x)ψ(x)二阶可导，且φ′(x)≠0\varphi'(x)≠0φ′(x)=0，则d2ydx2=ddt(ψ′(t)φ′(t))×1φ(′t)=ϕ′′(x)φ′(t)−φ′′(t)ϕ′(t)ϕ′3(x)\frac{d^2y}{dx^2}=\frac{d}{dt}(\frac{\psi'(t)}{\varphi'(t)})\times\frac{1}{\varphi('t)}=\frac{\phi''(x)\varphi'(t)-\varphi''(t)\phi'(t)}{\phi'^3(x)}dx2d2y​=dtd​(φ′(t)ψ′(t)​)×φ(′t)1​=ϕ′3(x)ϕ′′(x)φ′(t)−φ′′(t)ϕ′(t)​。

对数求导法

如果y=f(x)y=f(x)y=f(x)的表达式由多个因式的乘除、幂等构成，或是幂指函数的形式，则可先将函数取对数，然后两边对x求导。

高阶导数

概念

如果y=f′(x)y=f'(x)y=f′(x)作为xxx的函数在点xxx可导，则称y′y'y′的导数为y=f(x)y=f(x)y=f(x)的二阶导数，记为y′′y''y′′，或f′′(x)f''(x)f′′(x)，或d2ydx2\frac{d^2y}{dx^2}dx2d2y​。一般的，函数y=f(x)y=f(x)y=f(x)的n阶导数为y(n)=[f(n−1)(x)]y^{(n)}=[f^{(n-1)}(x)]y(n)=[f(n−1)(x)]，即nnn阶导数就是n−1n-1n−1阶导函数的导数。

常用的高阶导数公式

• (sinx)(n)=sin(x+n×π2)(sinx)^{(n)}=sin(x+n\times\frac{\pi}{2})(sinx)(n)=sin(x+n×2π​)
• (cosx)(n)=cos(x+n×π2)(cosx)^{(n)}=cos(x+n\times\frac{\pi}{2})(cosx)(n)=cos(x+n×2π​)
• (u±v)(n)=u(n)±v(n)(u\pm v)^{(n)}=u^(n)\pm v^{(n)}(u±v)(n)=u(n)±v(n)
• (uv)(n)=(uv)^{(n)}=(uv)(n)=∑k=0nCnku(k)v(n−k)\sum_{k=0}^n C_n^ku^{(k)}v^{(n-k)}∑k=0n​Cnk​u(k)v(n−k)

微分中值定理和导数的应用

微分中值定理用于建立函数和导数的联系。

微分中值定理

函数和111阶导数的关系：

• 费马引理：设函数f(x)f(x)f(x)在点x0x_0x0​处可导，如果函数f(x)f(x)f(x)在点x0x_0x0​处取得极值，那么f′(x0)=0f'(x_0)=0f′(x0​)=0。
• 罗尔定理：如果f(x)f(x)f(x)在闭区间[a,b][a,b][a,b]上连续，在开区间(a,b)(a,b)(a,b)内可导，f(a)=f(b)f(a)=f(b)f(a)=f(b)，则在(a,b)(a,b)(a,b)内至少存在一点ξ\xiξ，使f′(ξ)=0f'(\xi)=0f′(ξ)=0。
• 拉格朗日中值定理：如果f(x)f(x)f(x)在闭区间[a,b][a,b][a,b]上连续，在开区间(a,b)(a,b)(a,b)内可导，则在(a,b)(a,b)(a,b)内至少存在一点ξ\xiξ，使得f(b)−f(a)=f′(ξ)(b−a)f(b)-f(a)=f'(\xi)(b-a)f(b)−f(a)=f′(ξ)(b−a)。
• 柯西中值定理：如果f(x),F(x)f(x),F(x)f(x),F(x)在闭区间[a,b][a,b][a,b]上连续，在开区间(a,b)(a,b)(a,b)内可导，且F′(x)F'(x)F′(x)在(a,b)(a,b)(a,b)内每一点处均不为零，则在(a,b)(a,b)(a,b)内至少存在一点ξ\xiξ，使得f(b)−f(a)F(b)−F(a)=f′(ξ)F′(ξ)\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}F(b)−F(a)f(b)−f(a)​=F′(ξ)f′(ξ)​。

函数和nnn阶导数的关系：

• 皮亚诺型余项泰勒公式（局部泰勒公式，在x0x_0x0​临近处代替误差小）：如果f(x)f(x)f(x)在x0x_0x0​处有nnn阶导数，则f(x)=f(x0)+f′(x0)(x−x0)+...+1n!f(n)(xn)(x−x0)n+Rn(x)f(x)=f(x_0)+f'(x_0)(x-x_0)+...+\frac{1}{n!}f^{(n)}(x_n)(x-x_0)^n+R_n(x)f(x)=f(x0​)+f′(x0​)(x−x0​)+...+n!1​f(n)(xn​)(x−x0​)n+Rn​(x)常称Rn(x)=o[(x−x0)n](x→x0)R_n(x)=o[(x-x_0)^n](x\to x_0)Rn​(x)=o[(x−x0​)n](x→x0​)为皮亚诺型余项，若x0=0x_0=0x0​=0，则得麦克劳林公式：f(x)=f(0)+f′(0)x+12!f′′(0)x2+...+1n!f(n)(0)xn+o(xn)f(x)=f(0)+f'(0)x+\frac{1}{2!}f''(0)x^2+...+\frac{1}{n!}f^{(n)}(0)x^n+o(x^n)f(x)=f(0)+f′(0)x+2!1​f′′(0)x2+...+n!1​f(n)(0)xn+o(xn)
• 拉格朗日型余项泰勒公式（整体泰勒公式，在一个大的范围内代替误差小）：设函数f(x)f(x)f(x)在含有x0x_0x0​的开区间(a,b)(a,b)(a,b)内有n+1n+1n+1阶导数，则当x∈(a,b)x∈(a,b)x∈(a,b)时有f(x)=f(x0)+f′(x0)(x−x0)+...+1n!f(n)(xn)(x−x0)n+Rn(x)f(x)=f(x_0)+f'(x_0)(x-x_0)+...+\frac{1}{n!}f^{(n)}(x_n)(x-x_0)^n+R_n(x)f(x)=f(x0​)+f′(x0​)(x−x0​)+...+n!1​f(n)(xn​)(x−x0​)n+Rn​(x)其中Rn(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1(ξ介于x0与x之间)R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}(\xi介于x_0与x之间)Rn​(x)=(n+1)!f(n+1)(ξ)​(x−x0​)n+1(ξ介于x0​与x之间)，称为拉格朗日余项。

几个常用的泰勒公式如下：

• ex=1+x+x22!+⋯+xnn!+o(xn)e^x=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+o({x^n})ex=1+x+2!x2​+⋯+n!xn​+o(xn)
• sinx=x−x33!+⋯+(−1)n−1+x2n−1(2n−1)!+o(x2n−1)sinx=x-\frac{x^3}{3!}+\cdots+(-1)^{n-1}+\frac{x^{2n-1}}{(2n-1)!}+o({x^{2n-1}})sinx=x−3!x3​+⋯+(−1)n−1+(2n−1)!x2n−1​+o(x2n−1)
• cosx=1−x22!+⋯+(−1)n+x2n(2n)!+o(x2n)cosx=1-\frac{x^2}{2!}+\cdots+(-1)^{n}+\frac{x^{2n}}{(2n)!}+o({x^{2n}})cosx=1−2!x2​+⋯+(−1)n+(2n)!x2n​+o(x2n)
• ln(1+x)=x−x22+⋯+(−1)n−1xnn+o(xn)ln(1+x)=x-\frac{x^2}{2}+\cdots+(-1)^{n-1}\frac{x^n}{n}+o(x^n)ln(1+x)=x−2x2​+⋯+(−1)n−1nxn​+o(xn)
• (1+x)n=1+ax+a(a−1)2!x2+⋯+a(a−1)⋯(a−n+1)n!xn+o(xn)(1+x)^n=1+ax+\frac{a(a-1)}{2!}x^2+\dots+\frac{a(a-1)\cdots(a-n+1)}{n!}x^n+o(x^n)(1+x)n=1+ax+2!a(a−1)​x2+⋯+n!a(a−1)⋯(a−n+1)​xn+o(xn)

导数的应用

函数的单调性

设f(x)f(x)f(x)在闭区间[a,b][a,b][a,b]上连续，在开区间(a,b)(a,b)(a,b)内可导：

• 若在(a,b)(a,b)(a,b)内f′(x)>0f'(x)>0f′(x)>0，则f(x)f(x)f(x)在[a,b][a,b][a,b]上单调增。
• 若在(a,b)(a,b)(a,b)内f′(x)<0f'(x)<0f′(x)<0，则f(x)f(x)f(x)在[a,b][a,b][a,b]上单调减。

函数的极值

设f(x)f(x)f(x)在点x0x_0x0​的某邻域内有定义，如果对于该邻域（端点是半邻域）内任何xxx，恒有f(x)≤f(x0)f(x)≤f(x_0)f(x)≤f(x0​)，则称x0x_0x0​为f(x)f(x)f(x)的一个极大值点，称f(x0)f(x_0)f(x0​)为f(x)f(x)f(x)的极大值，极大值极小值统称为极值，极大值极小值点统称为极值点。

• 极值的必要条件：设f(x)f(x)f(x)在点x0x_0x0​处可导，如果点x0x_0x0​为f(x)f(x)f(x)的极值点，则f′(x0)=0f'(x_0)=0f′(x0​)=0。导数为零的点称为函数的驻点。
• 极值的第一充分条件：设f(x)f(x)f(x)在点x0x_0x0​的某去心邻域内可导，且f′(x0)=0f'(x_0)=0f′(x0​)=0或f(x)f(x)f(x)在x0x_0x0​处连续：
  • 若x0,x>x0f'(x)>0,x>x_0f′(x)>0,x>x0​时，f′(x)<0f'(x)<0f′(x)<0，则x0x_0x0​为f(x)f(x)f(x)的极大值点；
  • 若xx0f'(x)<0,x>x_0f′(x)<0,x>x0​时，f′(x)>0f'(x)>0f′(x)>0，则x0x_0x0​为f(x)f(x)f(x)的极小值点；
  • 若f′(x)f'(x)f′(x)在x0x_0x0​的两侧同号，则x0x_0x0​不为f(x)f(x)f(x)的极值点。
• 极值的第二充分条件：设f(x)f(x)f(x)在点x0x_0x0​处二阶可导，且f′(x0)=0f'(x_0)=0f′(x0​)=0：
  • 若f′′(x0)<0f''(x_0)<0f′′(x0​)<0，则x0x_0x0​为f(x)f(x)f(x)的极大值点；
  • 若f′′(x0)>0f''(x_0)>0f′′(x0​)>0，则x0x_0x0​为f(x)f(x)f(x)的极小值点；
  • 若f′′(x)=0f''(x)=0f′′(x)=0，则此方法不能判定x0x_0x0​是否为极值点。

函数的最大值和最小值

设函数f(x)f(x)f(x)在区间[a,b][a,b][a,b]上有定义，x0∈[a,b]x_0∈[a,b]x0​∈[a,b]，若对于任意x∈[a,b]x∈[a,b]x∈[a,b]，恒有f(x)≤f(x0)f(x)≤f(x_0)f(x)≤f(x0​)，则称f(x0)f(x_0)f(x0​)为函数的f(x)f(x)f(x)在区间[a,b][a,b][a,b]最大值，称x0x_0x0​为f(x)f(x)f(x)在区间[a,b][a,b][a,b]上的最大值点。

曲线的凹凸性

设函数f(x)f(x)f(x)在区间III上连续，如果对III上任意两点x1,x2x_1,x_2x1​,x2​恒有f(x1+x22)f(x1)+f(x2)2f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2}f(2x1​+x2​​)>2f(x1​)+f(x2​)​，则称f(x)f(x)f(x)在III上的图形是凸的；

• 拐点：连续曲线上的凹与凸的分界点称为曲线弧的拐点。
• 拐点的必要条件：设函数f(x)f(x)f(x)在点x0x_0x0​处二阶可导，且点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))为曲线f(x)f(x)f(x)的拐点，则f′′(x0)=0f''(x_0)=0f′′(x0​)=0。
• 拐点的第一充分条件：设f(x)f(x)f(x)在点x0x_0x0​的某去心邻域内二阶可导，且f′′(x0)=0f''(x_0)=0f′′(x0​)=0或f(x)f(x)f(x)在x0x_0x0​处连续：
  • 若f′′(x)f''(x)f′′(x)在x0x_0x0​的两侧异号，则点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))为曲线f(x)f(x)f(x)的拐点。
  • 若f′′(x)f''(x)f′′(x)在x0x_0x0​的两侧同号，则点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))不为曲线f(x)f(x)f(x)的拐点。
• 拐点的第二充分条件：设f(x)f(x)f(x)在点x0x_0x0​处三阶可导，且f′′(x0)=0f''(x_0)=0f′′(x0​)=0：
  • 若f′′′(x0)≠0f'''(x_0)≠0f′′′(x0​)=0，则点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))为曲线f(x)f(x)f(x)的拐点。
  • 若f′′′(x0)=0f'''(x_0)=0f′′′(x0​)=0，则此方法不能判定点(x0,f(x0))(x_0,f(x_0))(x0​,f(x0​))是否为曲线f(x)f(x)f(x)的拐点。

曲线的渐近线

若点M沿曲线f(x)f(x)f(x)无限远离原点时，它与某条定直线L之间的距离将趋近于零，则 称直线L为曲线f(x)f(x)f(x)的一条渐近线，若直线L与x轴平行，则称L为曲线y=f(x)y=f(x)y=f(x)的水平渐近线；若直线L与x轴垂直，则称L为曲线y=f(x)y=f(x)y=f(x)的垂直渐近线；若直线L既不平行于x轴，也不垂直于x轴，则称L为f(x)f(x)f(x)的斜渐近线。

• 水平渐近线：若lim⁡x→∞f(x)=A\lim\limits_{x\to \infty}f(x)=Ax→∞lim​f(x)=A或lim⁡x→−∞f(x)=A\lim\limits_{x\to -\infty}f(x)=Ax→−∞lim​f(x)=A或lim⁡x→+∞f(x)=A\lim\limits_{x\to +\infty}f(x)=Ax→+∞lim​f(x)=A，那么y=Ay=Ay=A是曲线y=f(x)y=f(x)y=f(x)的水平渐近线。
• 垂直渐近线：若lim⁡x→x0f(x)=∞\lim\limits_{x\to x_0}f(x)=\inftyx→x0​lim​f(x)=∞或lim⁡x→−x0−f(x)=∞\lim\limits_{x\to -x_0^-}f(x)=\inftyx→−x0−​lim​f(x)=∞或lim⁡x→+x0+f(x)=∞\lim\limits_{x\to +x_0^+}f(x)=\inftyx→+x0+​lim​f(x)=∞，那么x=x0x=x_0x=x0​是曲线y=f(x)y=f(x)y=f(x)的垂直渐近线。
• 斜渐近线：若lim⁡x→∞f(x)x=a\lim\limits_{x\to\infty}\frac{f(x)}{x}=ax→∞lim​xf(x)​=a且lim⁡x→∞(f(x)−ax)=b(或x→−∞或x→+∞)\lim\limits_{x\to \infty}(f(x)-ax)=b(或x\to -\infty或x \to +\infty)x→∞lim​(f(x)−ax)=b(或x→−∞或x→+∞)，那么y=ax+by=ax+by=ax+b是曲线y=f(x)y=f(x)y=f(x)的斜渐近线。

曲线的弧微分和曲率

• 弧微分：设函数f(x)f(x)f(x)在(a,b)(a,b)(a,b)内有连续导数，则有弧微分ds=1+y′2dxds=\sqrt{1+y^{'2}}dxds=1+y′2​dx。
• 曲率：设函数f(x)f(x)f(x)有二阶导数，则有曲率K=∣y′′∣(1+y′2)3/2K=\frac{|y''|}{(1+y^{'2})^{3/2}}K=(1+y′2)3/2∣y′′∣​，称p=1Kp=\frac{1}{K}p=K1​为曲率半径。
• 曲率圆：若曲线f(x)f(x)f(x)在点M(x,y)M(x,y)M(x,y)处的曲率为K(K≠0)K(K≠0)K(K=0)，在点M处曲线的法线上，在曲线凹的一侧取一点D，使∣DM∣=1K=p|DM|=\frac{1}{K}=p∣DM∣=K1​=p，以D为圆心，以p为半径的圆称为曲线在点M处的曲率圆，圆心D为曲线在点M处的曲率中心。