计算机图形学08:中点BH算法绘制抛物线(100x = y^2)
创始人
2024-05-30 00:55:31
0次

作者:非妃是公主
专栏:《计算机图形学》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
文章目录
- 专栏推荐
- 专栏系列文章
- 序
- 一、算法原理
- 二、OpenGL代码实现
- 三、效果展示
- the end……
专栏推荐
| 专栏名称 | 专栏地址 |
|---|---|
| 软件工程 | 专栏——软件工程 |
| 计算机图形学 | 专栏——计算机图形学 |
| 操作系统 | 专栏——操作系统 |
| 软件测试 | 专栏——软件测试 |
| 机器学习 | 专栏——机器学习 |
| 数据库 | 专栏——数据库 |
| 算法 | 专栏——算法 |
专栏系列文章
| 文章名称 | 文章地址 |
|---|---|
| 直线生成算法(DDA算法) | 计算机图形学01——DDA算法 |
| 中点BH算法绘制直线 | 计算机图形学02——中点BH算法 |
| 改进的中点BH算法 | 计算机图形学03——改进的中点BH算法 |
| 中点Bresenham画椭圆 | 计算机图形学04——中点BH绘制椭圆 |
| 中点BH算法绘制任意斜率直线 | 计算机图形学05——中点BH算法绘制任意斜率的直线 |
| 中点Bresenham画圆 | 计算机图形学06——中点BH算法画圆 |
| 有效边表法的多边形扫描转换 | 计算机图形学07——有效边表法绘制填充多边形 |
| 中点BH算法绘制抛物线 100x=y2100x = y^2100x=y2 | 计算机图形学08——中点BH绘制抛物线 |
| 二维观察之点的裁剪 | 计算机图形学09——二维观察之点裁剪 |
| 二维观察之线的裁剪 | 计算机图形学10——二维观察之线裁剪 |
| 二维观察之多边形的裁剪 | 计算机图形学11——二维观察之多边形裁剪 |
| 二维图形的几何变换 | 计算机图形学12——二维图形几何变换 |
| 三维图形的几何变换 | 计算机图形学13——三维图形几何变换 |
| 三维图形的投影变换 | 计算机图形学14——三维图形投影变换 |
序
计算机图形学(英语:computer graphics,缩写为CG)是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科,是计算机科学的一个分支领域,主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形,事实上同时包括了二维图形以及影像处理。
一、算法原理
首先,基本思路还是将抛物线分为斜率 k≥1k\geq1k≥1 和 k<1k<1k<1 两种情况。
左边为 k>1k>1k>1 的情况(针对本问题 x≤25x\leq25x≤25),右边为 k<1k<1k<1 的情况(x>25)。
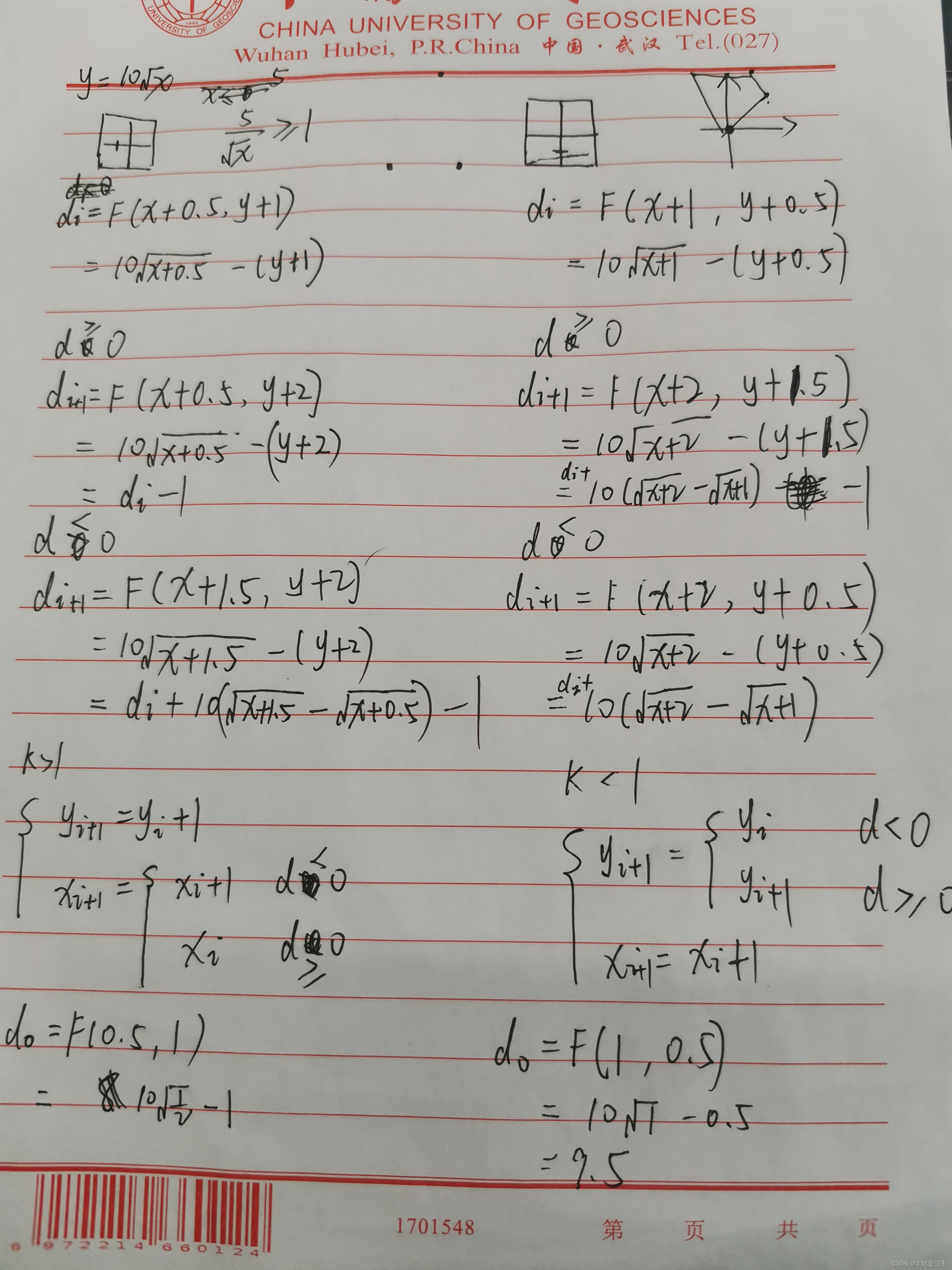
二、OpenGL代码实现
// 绘制抛物线 100*x = y^2
void MidBhParabola() {int x = 0;int y = 0;double d = 10 / sqrt(2) - 1;// 开始绘制glColor3f(0.0f, 1.0f, 0.0f); // 设置颜色为绿色进行填充glBegin(GL_POINTS);glVertex2i(x, y); // 绘制(0, 0)点// k>1 的情况while (x <= 25) { // 更新dif (d < 0) {d += 10 * (sqrt(x + 1.5) - sqrt(x + 0.5)) - 1;}else {d -= 1;}y++;// 根据 d 的值更新xif (d < 0) {x++;}glVertex2i(x, y);glVertex2i(x, -y); // 二分画圆}// k<=1的情况d = 10 * sqrt(25 + 1) - (50 + 0.5);while (x <= 250) {// 更新dif (d < 0) {d += 10 * (sqrt(x + 2) - sqrt(x + 1));}else {d += 10 * (sqrt(x + 2) - sqrt(x + 1.5)) - 1;}// 更新x,yx++;if (d >= 0) {y++;}glVertex2i(x, y);glVertex2i(x, -y); // 二分画抛物线}glEnd();
}
三、效果展示
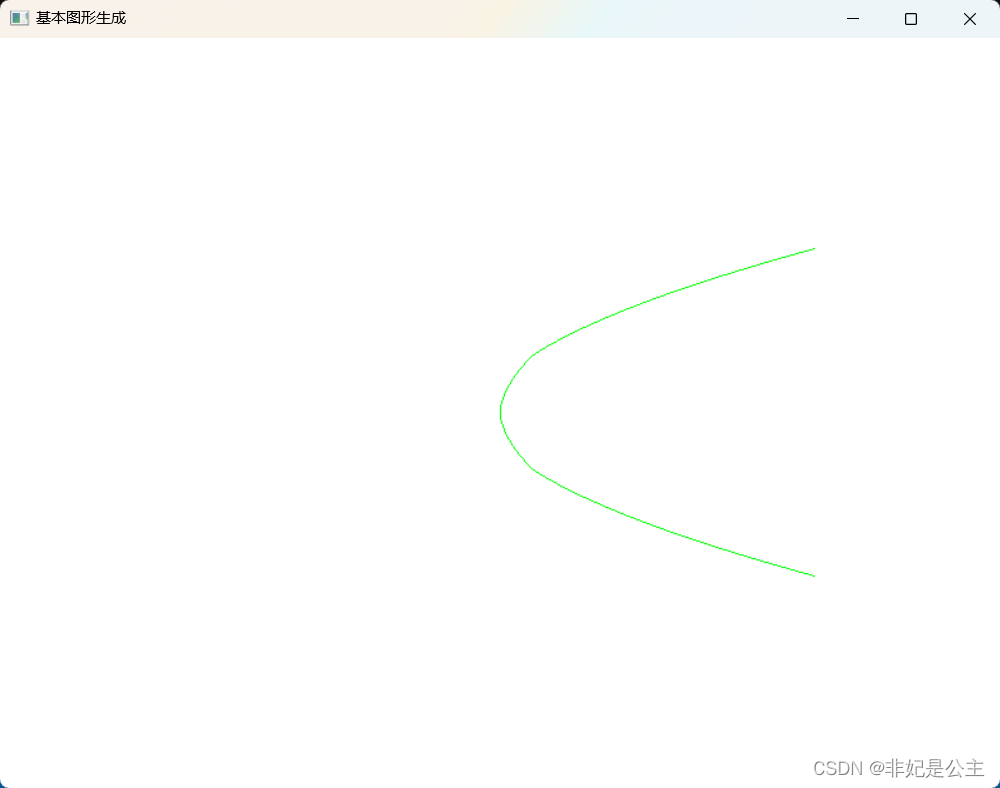
the end……
有效边表法的多边形扫描转换算法到这里就要结束啦~~到此既是缘分,欢迎您的点赞、评论、收藏!关注我,不迷路,我们下期再见!!
😘😘😘 我是Cherries,一位计算机科班在校大学生,写博客用来记录自己平时的所思所想!
💞💞💞 内容繁杂,又才疏学浅,难免存在错误,欢迎各位大佬的批评指正!
👋👋👋 我们相互交流,共同进步!
注:本文由
非妃是公主发布于https://blog.csdn.net/myf_666,转载请务必标明原文链接:https://blog.csdn.net/myf_666/article/details/128234564
相关内容
热门资讯
电视安卓系统哪个品牌好,哪家品...
你有没有想过,家里的电视是不是该升级换代了呢?现在市面上电视品牌琳琅满目,各种操作系统也是让人眼花缭...
安卓会员管理系统怎么用,提升服...
你有没有想过,手机里那些你爱不释手的APP,背后其实有个强大的会员管理系统在默默支持呢?没错,就是那...
安卓系统软件使用技巧,解锁软件...
你有没有发现,用安卓手机的时候,总有一些小技巧能让你玩得更溜?别小看了这些小细节,它们可是能让你的手...
安卓系统提示音替换
你知道吗?手机里那个时不时响起的提示音,有时候真的能让人心情大好,有时候又让人抓狂不已。今天,就让我...
安卓开机不了系统更新
手机突然开不了机,系统更新还卡在那里,这可真是让人头疼的问题啊!你是不是也遇到了这种情况?别急,今天...
安卓系统中微信视频,安卓系统下...
你有没有发现,现在用手机聊天,视频通话简直成了标配!尤其是咱们安卓系统的小伙伴们,微信视频功能更是用...
安卓系统是服务器,服务器端的智...
你知道吗?在科技的世界里,安卓系统可是个超级明星呢!它不仅仅是个手机操作系统,竟然还能成为服务器的得...
pc电脑安卓系统下载软件,轻松...
你有没有想过,你的PC电脑上安装了安卓系统,是不是瞬间觉得世界都大不一样了呢?没错,就是那种“一机在...
电影院购票系统安卓,便捷观影新...
你有没有想过,在繁忙的生活中,一部好电影就像是一剂强心针,能瞬间让你放松心情?而我今天要和你分享的,...
安卓系统可以写程序?
你有没有想过,安卓系统竟然也能写程序呢?没错,你没听错!这个我们日常使用的智能手机操作系统,竟然有着...
安卓系统架构书籍推荐,权威书籍...
你有没有想过,想要深入了解安卓系统架构,却不知道从何下手?别急,今天我就要给你推荐几本超级实用的书籍...
安卓系统看到的炸弹,技术解析与...
安卓系统看到的炸弹——揭秘手机中的隐形威胁在数字化时代,智能手机已经成为我们生活中不可或缺的一部分。...
鸿蒙系统有安卓文件,畅享多平台...
你知道吗?最近在科技圈里,有个大新闻可是闹得沸沸扬扬的,那就是鸿蒙系统竟然有了安卓文件!是不是觉得有...
宝马安卓车机系统切换,驾驭未来...
你有没有发现,现在的汽车越来越智能了?尤其是那些豪华品牌,比如宝马,它们的内饰里那个大屏幕,简直就像...
p30退回安卓系统
你有没有听说最近P30的用户们都在忙活一件大事?没错,就是他们的手机要退回安卓系统啦!这可不是一个简...
oppoa57安卓原生系统,原...
你有没有发现,最近OPPO A57这款手机在安卓原生系统上的表现真是让人眼前一亮呢?今天,就让我带你...
安卓系统输入法联想,安卓系统输...
你有没有发现,手机上的输入法真的是个神奇的小助手呢?尤其是安卓系统的输入法,简直就是智能生活的点睛之...
怎么进入安卓刷机系统,安卓刷机...
亲爱的手机控们,你是否曾对安卓手机的刷机系统充满好奇?想要解锁手机潜能,体验全新的系统魅力?别急,今...
安卓系统程序有病毒
你知道吗?在这个数字化时代,手机已经成了我们生活中不可或缺的好伙伴。但是,你知道吗?即使是安卓系统,...
奥迪中控安卓系统下载,畅享智能...
你有没有发现,现在汽车的中控系统越来越智能了?尤其是奥迪这种豪华品牌,他们的中控系统简直就是科技与艺...

