文章目录

• A. Likes【贪心、模拟】
• B. Settlement of Guinea Pigs【贪心】
• C. The Very Beautiful Blanket【构造、观察】

A. Likes【贪心、模拟】

分析
为了使得当前时间点赞的尽可能大，那么前面的赞的数目也要尽可能大，所以前面把能赞的都要先赞上，尽管后面撤赞了也使得其相对更大。为了使得每个点的赞仅可能小，前面留下的赞也要仅可能小，所以前面赞完之后马上要撤赞，即使后面不得不要点赞也可以保证此时最小。只需要模拟一下即可，统计一下，只赞不撤和又赞又撤的情况数目，模拟一下即可。
实现

#include 
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1) 
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair PII;
const int N = 1005, M = 1e6 + 5;
int a[N], b[N];
void solve() {int n;cin >> n;for (int i = 1; i <= n; i++) a[i] = b[i] = 0;for (int i = 1; i <= n; i++) {int c;cin >> c;if (c > 0) a[c] = 1;else b[-c] = 1;}int cnt1 = 0, cnt2 = 0;for (int i = 1; i <= n; i++) {if (a[i] && !b[i]) cnt1++;//只赞if (a[i] && b[i]) cnt2++; //又赞又撤}int p = 0, t1 = cnt1 + cnt2, t2 = cnt2;//t1表示前面递增的长度for (int i = 1; i <= n; i++) {if (i != 1) cout << ' ';if (t1) cout << ++p, t1--;else if (t2) cout <<  --p, t2--;}cout << '\n';int m1 = 2 * cnt2, m2 = cnt1, q = 0;//m1表示前面又赞又撤的长度for (int i = 1; i <= n; i++) {if (i != 1) cout << ' ';if (i <= m1) {cout << (i & 1 ? 1 : 0);} else {cout << ++q;}}cout << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) {solve();}
}

B. Settlement of Guinea Pigs【贪心】

分析
这题本身不难。创建两个变量，cnt表示当前的豚鼠的数目，tmp表示最坏的情况（至少需要多少个笼子），如果说医生还没有来的话，多一个豚鼠，就需要多一个笼子，如果医生来的话就可以鉴定了，例如我们有100只豚鼠，性别已知，数目情况下数目最多，答案是一只异性，其余同性，1 + (99 + 1) / 2，共需要51个笼子，为什么呢？可以这样想，对于装满两只的笼子，这个笼子里是什么性别并不重要，反正是装满了，所以多余所有的情况都可以转化位，要么全部同性，要么有一只异性，全部同性，可能是有一个是一只笼子的，这样把他转话为异性，也不会增加笼子数，刚好整装，那么有一个异性则是可以增加一个笼子，为了确保这样的情况，所以我们就单取出一只异性即可。
实现

#include 
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1) 
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair PII;
const int N = 1005, M = 1e6 + 5;
void solve() {int n;cin >> n;int ans = 0, cnt = 0, tmp = 0;for (int i = 1; i <= n; i++) {int c;cin >> c;if (c == 1) cnt++, tmp++;else {if (cnt) {tmp = 1 + cnt / 2;}}ans = max(tmp, ans);}cout << ans << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) {solve();}
}

C. The Very Beautiful Blanket【构造、观察】

分析
乍一看，你可能觉得这是什么用脚造的数据，太毒瘤了，但是实际上不是的。

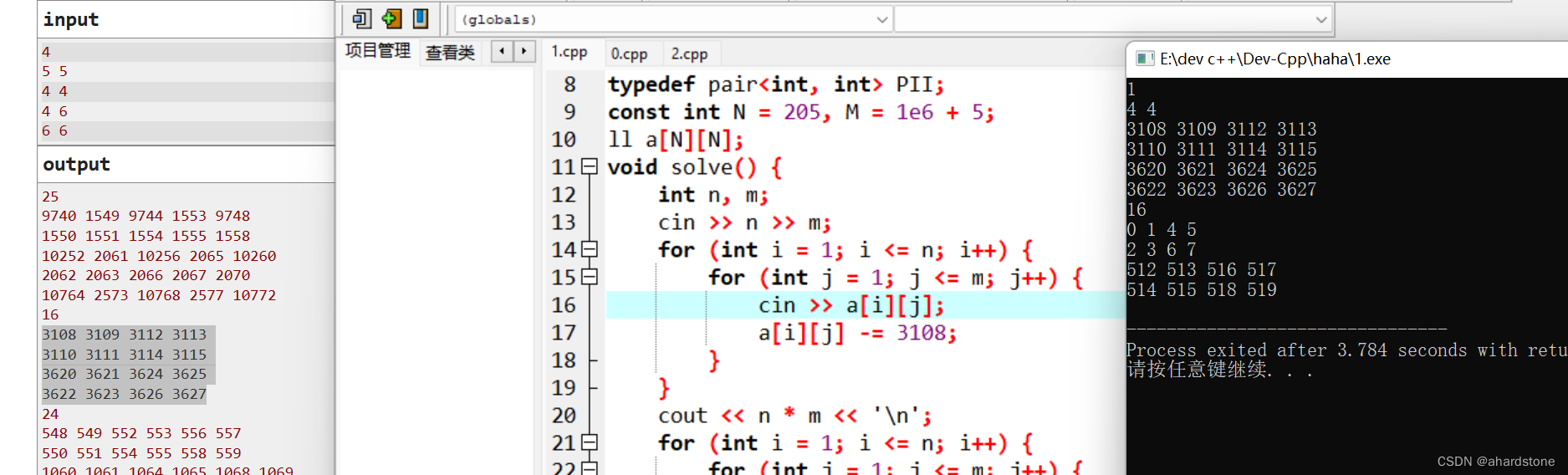
观察一下我们就可以发现，每个数都是由一个子矩阵
0 1
2 3
加上一个数得到的，我们还可以发现所有的2*2的矩阵异或和都为零。那么加多少呢
如果说，我们不考虑数不能重复，那么我们可以这样构造。
0 1 0 1 0 1
2 3 2 3 2 3
0 1 0 1 0 1
2 3 2 3 2 3
对于相邻两个我们加多少合适，写成二进制。
000 001 100 101
010 011 110 111
可以发现，加4是合理的，对于中间四个而言，4的那一位是独立的，
0 4
0 4 这样对应位的异或和也是0，一位4的位数比较高，而且不影响末尾的0 1 2 3，那么下一行加多少呢，由于有200列，我们选择加一个大的2的幂，不影响最低位。
对于加粗部分的矩阵，虽然每两行之间是有差值的，但是两列（奇数列（1,3,5列）在前）之间必然是1，一个是偶数，一个是对应偶数加1，异或之后就是1。两个1异或就是0。另外的奇数列在前就是上面加4的情况，即使这两行不是奇数行在前，由于同行加的高位的2的幂是相同的异或会抵消，就相当于
0 4
0 4
完毕。
实现

#include 
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1) 
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair PII;
const int N = 205, M = 1e6 + 5;
ll a[N][N];
void solve() {int n, m;cin >> n >> m;a[1][1] = 0, a[1][2] = 1;a[2][1] = 2, a[2][2] = 3;for (int j = 3; j <= m; j++) {a[1][j] = a[1][j - 1] + 4;a[2][j] = a[2][j - 1] + 4; }for (int i = 3; i <= n; i++) {for (int j = 1; j <= m; j++) {a[i][j] = a[i - 2][j] + 4096;}}cout << n * m << '\n';for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << a[i][j] << " \n"[j == m];}}
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) {solve();}
}
/*
1
4 4
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15 
*/