一、问题描述

羽毛球队有男女运动员各n人。给定2个n×n矩阵P和Q。
P[i][j]是男运动员i的女运动员j配对组成混合双打的男运动员竞赛优势；Q[i][j]是女运动员i和男运动员j配对的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响，P[i][j]不一定等于Q[i][j]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]×Q[i][j]。
设计一个算法，计算男女运动员最佳配对法，使各组男女双方竞赛优势的总和达到最大。
输入样例：（第一行是男队员（或女队员）的个数，第二、三、四行是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势，第五、六、七行是女运动员i和男运动员j配合的女运动员竞赛优势）
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
输出样例：（第一行是竞赛优势的最大和）
52

二、算法思路

固定男运动员，对女运动员进行一次全排列，并求出每位男运动员能匹配到的最大优势值。本题共有n！种配对情况。

固定1号男运动员，让所有的n个女运动员与其匹配，经过n次匹配，分别保存每组男女运动员的匹配优势到res数组和最优的男女运动员优势到MaxSum数组。
其中，res数组是N×N的二维数组，用于保存每个男运动员匹配过的女运动员的优势；MaxSum是一个1×N的一维数组，用于保存每个男运动员的匹配的最佳女运动员的优势。

根据题目的输入样例可以得到以下的排列树：

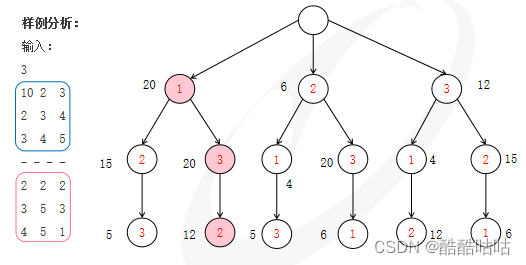
固定男运动员选女运动员，构成一颗排列数。树的第i行表示第i个男运动员，树结点序号表示与当前行男运动员匹配的女运动员序号。如：第一行的1表示，第一个男运动员与第一个女运动员匹配的竞争优势是20。

剪枝策略

如下是第一步计算得到的MaxSum和res数组：

如下是第一个分支进行搜索的过程：

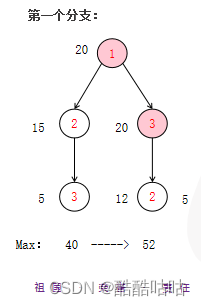
当搜索该子树时，Max=40，表示已经探索过的路线中得到的最优解是40。

此时，在该层进行剪枝的判断：
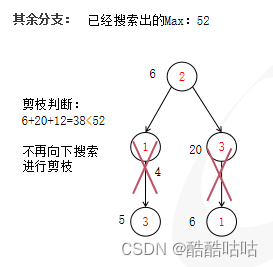
已经固定的运动员优势和为20+20=40，假设再贪心的加上剩下的运动员匹配优势的最大值为40+MaxSum[2]=40+12=52, 52>40,则还有可能得到更大的优势解，继续向下搜索。

若贪心的加上其余运动员匹配最大优势后，仍不能超过已经搜索出的最优解，那么向下搜完整颗子树也不会得到最优解，则要进行剪枝操作。因为再向下搜索的结果只可能是小于等于最大优势的。
这就是【剪枝操作】的核心思想！

#include 
using namespace std;int n;
int boy[21][21], girl[21][21];
int Max = INT_MIN; //MAX代表男女双方竞赛优势的总和的最大值 用来返回指定整数类型所能表示的最小值。
int sum = 0;
int res[21][21]; //data[i][j]用于存放男运动员i配对后的双方竞赛优势
int maxSum[21];   //保存每个男生匹配后可达到的最大双方竞赛优势
int book[21];    //标记女运动员是否已经匹配 0未匹配 1已匹配//Max：40 -> 52
void dfs(int t){if(t>=n)  //t到达n后，代表全部标记访问了，得到了最大值{Max = max(Max, sum);return;}int cnt = 0;//求t及t之后男生匹配女生的最大值的和for (int i = t; i < n;i++){cnt += maxSum[i];//假设的贪心的让每个男运动员匹配最优的女运动员}//剪枝函数：之前t个已经匹配好的男女运动员的sum与//之后的t->n-1个男女匹配的最大值加起来得到的Max比较//若前者<=Max，剪枝if(sum+cnt=Max，要继续向下搜索//从第t个男生开始匹配，找未匹配的女生for (int i = 0; i < n;i++){if(!book[i]){//若第i个女生未匹配book[i] = 1;sum += res[t][i];dfs(t + 1);book[i] = 0; //若第t个男生匹配女生i得到的sum不大于Max，则回溯sum -= res[t][i];}}
}int main(){cin >> n;for (int i = 0; i < n;i++){for (int j = 0; j < n;j++){cin >> boy[i][j];}}for (int i = 0; i < n;i++){for (int j = 0; j < n;j++){cin >> girl[i][j];}}for (int i = 0; i < n;i++){for (int j = 0; j < n;j++){//对每个男生都求男女双方竞赛优势，能得到i*j种结果res[i][j] = boy[i][j] * girl[j][i];//记录每个男生匹配后可达到的最大双方竞赛优势，用于后面的剪枝maxSum[i] = max(maxSum[i], res[i][j]);}}dfs(0);cout << Max << endl;return 0;
}

参考博客：运动员最佳匹配问题【回溯算法】