Java JZ52 两个链表的第一个公共结点

文章目录

• Java JZ52 两个链表的第一个公共结点
• 一、描述
• 二、Set 解法
• 三、差值法
• 四、等值法

  使用Set 解法、差值法和等值法解决剑指offer 第JZ52题 两个链表的第一个公共结点的问题。

一、描述

  输入两个无环的单向链表，找出它们的第一个公共结点，如果没有公共节点则返回空。（注意因为传入数据是链表，所以错误测试数据的提示是用其他方式显示的，保证传入数据是正确的）

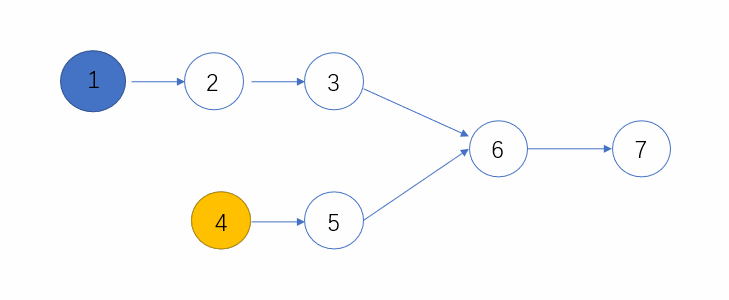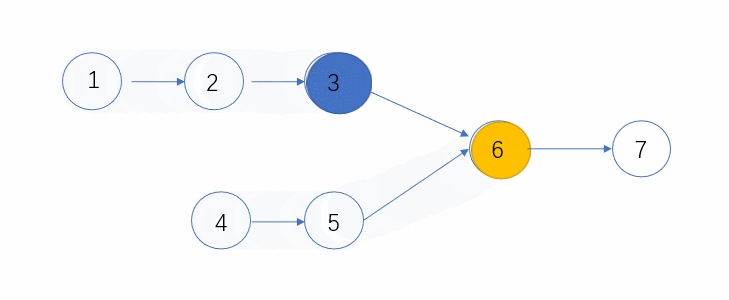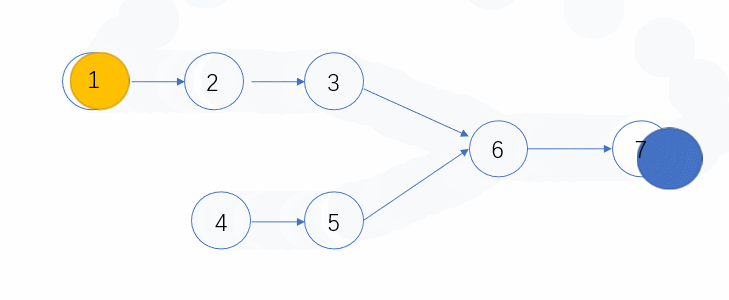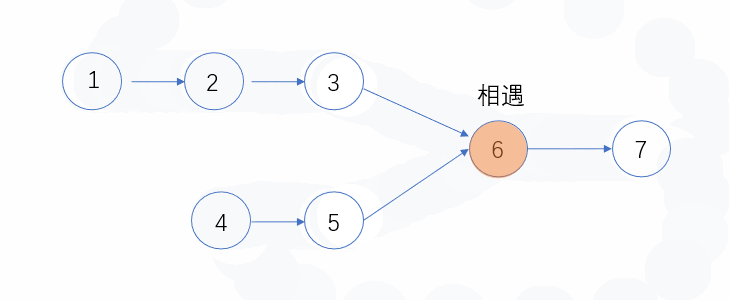
  例如，输入{1,2,3},{4,5},{6,7}时，两个无环的单向链表的结构如下图所示：

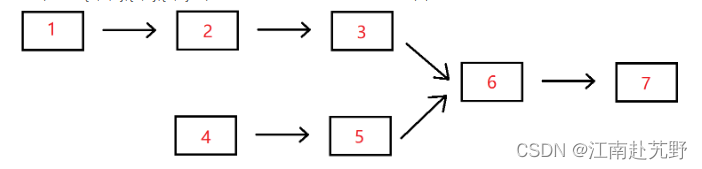
  可以看到它们的第一个公共结点的结点值为6，所以返回结点值为6的结点。
  输入描述：
  输入分为是3段，第一段是第一个链表的非公共部分，第二段是第二个链表的非公共部分，第三段是第一个链表和第二个链表的公共部分。 后台会将这3个参数组装为两个链表，并将这两个链表对应的头节点传入到函数FindFirstCommonNode里面，用户得到的输入只有pHead1和pHead2。
  返回值描述：
  返回传入的pHead1和pHead2的第一个公共结点，后台会打印以该节点为头节点的链表
  示例：

输入：
{1,2,3},{4,5},{6,7}
返回值：
{6,7}

二、Set 解法

  做这题最容易想到的一种解决方式就是先把第一个链表的节点全部存放到集合set中，然后遍历第二个链表的每一个节点，判断在集合set中是否存在，如果存在就直接返回这个存在的结点。如果遍历完了，在集合set中还没找到，说明他们没有相交，直接返回null即可，原理比较简单，直接看下代码

import java.util.HashSet;
/*
public class ListNode {int val;ListNode next = null;ListNode(int val) {this.val = val;}
}*/
public class Solution {public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {//判断pHead1 或者pHead2 是不是有一个为null，如果有就说明一定没有公共部分if (pHead1 == null || pHead2 == null) {return null;}//创建集合hashsetHashSet hashset = new HashSet();//复制pHead1和pHead2ListNode pNode1 = pHead1, pNode2 = pHead2;//将pNode1节点值依次放入集合hashsetwhile (pNode1 != null) {hashset.add(pNode1);pNode1 = pNode1.next;}
//遍历pNode2的节点值，看是否集合hashset 中有相同元素while (pNode2 != null) {if (hashset.contains(pNode2)) {return pNode2;}pNode2 = pNode2.next;}
//如果集合hashset不包含pNode2的任何一个结点，说明他们没有交点，直接返回nullreturn null;}
}

三、差值法

  由于两条链表在相交节点后面的部分完全相同，因此我们可以先对两条链表进行遍历，分别得到两条链表的长度，并计算差值 d。

  让长度较长的链表先走 d 步，然后两条链表同时走，第一个相同的节点即是节点。

import java.util.*;
public class Solution {public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {int c1 = 0, c2 = 0;ListNode ta = pHead1, tb = pHead2;//先得到两个链表的长度c1和c2while (ta != null && c1++ >= 0) ta = ta.next;while (tb != null && c2++ >= 0) tb = tb.next;//判断差值int d = c1 - c2;if (d > 0) {// 说明pHead1链表长，pHead1先走 d 步while (d-- > 0) pHead1 = pHead1.next;} else if (d < 0) {// 说明pHead2链表长，pHead2先走 d 步d = -d; //将负数转为整数while (d-- > 0) pHead2 = pHead2.next;}// 判断两个链表剩余的节点值是否相同while (pHead1 != pHead2) {pHead1 = pHead1.next;pHead2 = pHead2.next;}// 相同就返回剩余链表return pHead1;}
}

四、等值法

  这是解答区的答案，是我自己想不到的，题感还是不行，只能想到普通解法，一起观摩一下这个解法吧。
  使用两个指针N1,N2，一个从链表1的头节点开始遍历，我们记为N1，一个从链表2的头节点开始遍历，我们记为N2。

  让N1和N2一起遍历，当N1先走完链表1的尽头（为null）的时候，则从链表2的头节点继续遍历，同样，如果N2先走完了链表2的尽头，则从链表1的头节点继续遍历，也就是说，N1和N2都会遍历链表1和链表2。

  因为两个指针，同样的速度，走完同样长度（链表1+链表2），不管两条链表有无相同节点，都能够到达同时到达终点。（N1最后肯定能到达链表2的终点，N2肯定能到达链表1的终点）。

  所以，如何得到公共节点：

  有公共节点的时候，N1和N2必会相遇，因为长度一样嘛，速度也一定，必会走到相同的地方的，所以当两者相等的时候，则返会第一个公共的节点
  无公共节点的时候，此时N1和N2则都会走到终点，那么他们此时都是null，所以也算是相等了。
  下面看个动态图，可以更形象的表示这个过程~

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {ListNode l1 = pHead1, l2 = pHead2;while(l1 != l2){l1 = (l1==null)?pHead2:l1.next;l2 = (l2==null)?pHead1:l2.next;}return l1;}