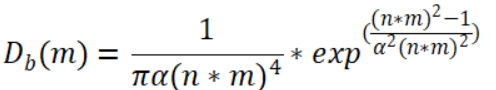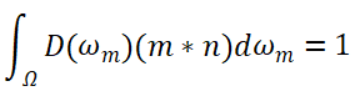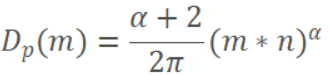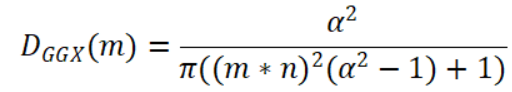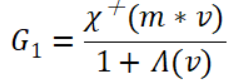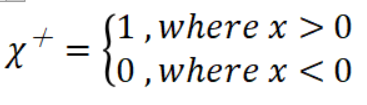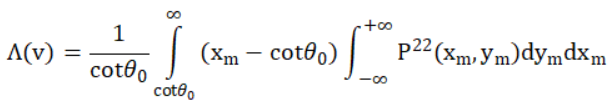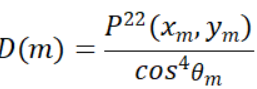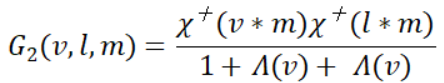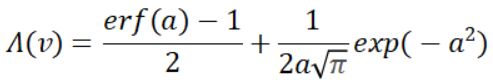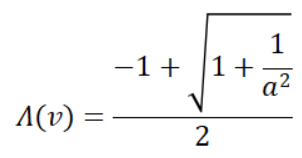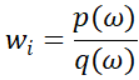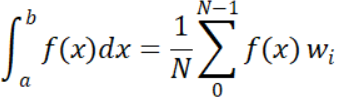这篇文章写于一年多以前的一次课程作业，这次作为一个“存货”给放出来，仅仅只是针对代码和一些要点进行简单叙述，如果想听完整的版本，请搜索毛星云大神的博客或者书籍。关于基本的物理渲染公式，网络上的博客和典籍已经多如牛毛了，这里只是自己在之前整理的结果上传。

 引言

如何对使用计算机图形基础构建出的面进行着色是计算机图形学的基本课题之一，为此，裴祥风提出了Phong氏光照模型，即对于一个表面，其漫反射光照值等于被照射平面的法线和光线组成的夹角的余弦，其高光反射值等于被照射平面的法线和光线入射与视角出射的组成半向量的余弦的幂函数。这个模型可以很好的描述非金属绝缘体的着色效果，但是对于具有金属性的导体则不能表达。为了渲染出更贴近于真实世界的图像效果，基于物理的渲染模型被提出并应用到图形着色上。Whitted,Turner在1980年首次提出来使用光线追踪来实现全局照明效果。而Cook和Terrance在1982年将微表面理论引入到图形学中，并提出了针对镜面高光的Cook-Terence 双向反射分布模型(Bidirectional Reflectance Distribution Function BRDF)，完整地描述了当一束光照到一个表面时通过观察角度能得到物理反射的值。再通过这些年来不断的引入新的法线分布方法和遮蔽方法，逐渐完善了物理渲染的知识体系。

对于一个标准的物理渲染模型而言，它必须遵循以下规则：

• 微平面理论：将物体表面建模成做无数微观尺度上有随机朝向的理想镜面反射的微平面。
• 能量守恒：出射光线的能量永远不能超过入射光线的能量。随着粗糙度的上升镜面反射区域的面积会增加，作为平衡，镜面反射区域的平均亮度则会下降。
• 遵循菲涅尔反射规律：光线以不同角度入射会有不同的反射率。相同的入射角度，不同的物质也会有不同的反射率。遵循以上规则的计算方程，我们称为渲染方程。

在描述一个表面（即一个点）的渲染方程，可以理解为漫反射和高光反射的加法。这个方程由Kajiya，James T.于1986年提出，以积分的方式描述了光在一个点上的流动方式：

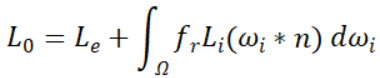
 其中Lo为出射光线的亮度，Le为p点自行发出的光亮度（自发光），fr为出射辐亮度与入射光辐照度的比值即BRDF，Li为p点由ωi方向入射的辐亮度。ωi * n表示为p点入射光与法线夹角的余弦，其数学意义是入射光的衰减。积分表示p点在法线方向的半球上的立体角积分。而Cook-Terrance的BRDF模型解决了fr的计算问题。使得对于计算机上的三维模型映射在屏幕上的每一个像素根据上述公式计算正确的渲染结果成为可能。

双向反射分布函数BRDF

双向反射分布函数描述的是一点上从表面入射的光线能量和表面出射的光线能量的比例关系，在辐射度学中表示为出射的辐亮度Lo(radiance)与入射的辐照度E(Irraiance)的比值。(这句话我认为是BRDF的KeyWord，差不多理解了这句话就能理解BRDF)。而针对一个点接受光的情况，常常分为直接光照的BRDF与间接光照的BRDF。

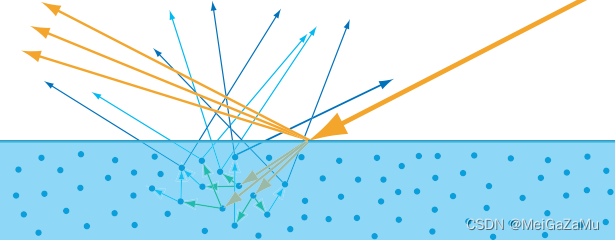
并且，根据物体的表面材质，光线在物体表面的反射现象可以划分为漫反射和镜面反射，指当光线从前一个介质传播到后一个介质时。一部分光线进入介质内部，并且经过若干次散射后再从介质表面发射出来的物理现象，这个现象即为光的漫反射，计算时可以近似看成是一个点向半球内每个立体角微分都发射同样强度的光线。所以可以用立体角积分计算它。而镜面反射则可以看成光线根据入射点的反射角度方向反射光线，其反射的波瓣取决于介质表面的光滑程度，并且，仅当观察者沿着某个特定的观察角度才能看见该反射光线。在计算BRDF时，漫反射BRDF与镜面反射BRDF都需要单独计算然后叠加。即：

其中，kd表示入射光被吸收的比率。ks表示入射光被反射的比率。这一点可以用菲涅尔系数和金属度来表示它们。在下文中将具体叙述Diffuse和Specular的BRDF。

漫反射的双向反射分布函数Diffuse BRDF

对于漫反射计算而言，其BRDF可以分为传统型和物理型，传统型仅仅是计算光线根据法线夹角计算衰减，即简单的Lambert模型。而物理型则有多种，例如Oren Nayar、Disney Diffuse、Gotanda Diffuse等。它们都遵循于漫反射时的辐照度公式：

其中E0为出射角的辐照度Irradiance，Ωout为表面法线为中轴线所在的半球。由于对于半球上的每个立体角微分而言，入射的漫反射光都是一致的，根据这一点可以直接算出Eo的值等于Lo*。进而可知对于每个漫反射的BRDF都需要除以π才能获得正确的值。

如果一个表面是纯Lambert表面，即Radiance向半球四周均匀地散射时，它的值与观察方向无关，所以BRDF是一个定值。这个值可以通过简单的积分算出来，即存在一个点的出射辐照度为：

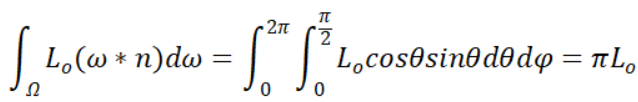
其中Lo为ω方向的光照，此时可以得知，均匀向半球发射的光照的总的辐照度等于某一方向的辐亮度乘以π：

设出射辐照度与入射辐照度的比值为C，即简单的有：

正好，BRDF的定义是入射辐照度Irradiance与出射辐亮度Radiance的比值，将上面两个式子代入，可以得出漫反射表面的BRDF函数：

其中， C为物体表面的albedo或者材质颜色（例如表面的漫反射TextureColor）。

同时，比较常见的漫反射计算方法还有Disney的漫反射计算方法，我自己试过之后会比原本的BRDF要亮一点点：

            float DisneyDiffuse(float3 worldNormal,float3 worldViewDir,float3 worldLight,float3 halfDir,float roughness){float PI=3.14159265;float cosLightNormal=saturate(dot(worldLight,worldNormal));float cosViewNormal=saturate(dot(worldViewDir,worldNormal));float cosViewHalf=saturate(dot(halfDir,worldLight));float F90=0.5+2*roughness*cosViewHalf*cosViewHalf;float FdV=1+(F90-1)*pow(1-cosViewNormal,5);float FdL=1+(F90-1)*pow(1-cosLightNormal,5);return FdL*FdV/PI;}

镜面反射的双向反射分布函数Specular BRDF

业界目前最常用的镜面BRDF模型的基于物理的镜面反射BRDF模型是基于微平面理论的MicrofacetCook-Torrance BRDF。

微平面理论源自将微观几何建模为微平面的集合的思想，一般用于描述非光学平坦的表面反射。微平面理论的基本假设是微观几何的存在，微观几何的尺度小于观察尺度（例如着色分辨率），但大于可见光波长的尺度（因此应用几何光学和如衍射一样的波效应等可以忽略）。在微平面理论下，物体表面可以看作是一系列细小的平面所构成的宏平面，这些微平面我们肉眼不可见，但是又远大于光的波长

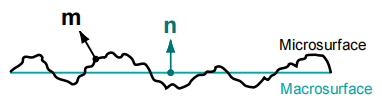
且由于假设微观几何尺度明显大于可见光波长，可以将每个宏观表面设为有统一法线n的平坦表面，而该表面将入射光线分为反射和折射两个方向。

每个微表面将来自给定进入方向的光反射到单个出射方向，该方向取决于微观几何法线m的方向。 在计算BRDF时，指定入射方向l和出射方向v。 这意味着所有表面点，只有那些恰好正确朝向可以将l反射到v的微平面可能有助于BRDF值（其他方向有正有负，积分之后，相互抵消）。

一个宏观平面中必定存在一些微平面法线m正好位于l和v之间的中间位置。l和v之间的矢量称为半矢量或半角矢量，这个向量最初来源于Phong模型用于加速计算 一般将其表示为h。h定义为：

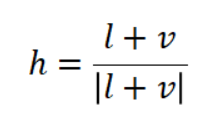
 如下图：

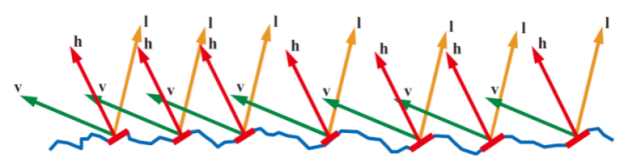
一般使用法线分布函数NDF(Normal Distribution Function)来得到法线为h的微观平面在宏观平面中所占的比例。需要注意的是，微平面理论模型没有考虑明显的波光学效应，如衍射和干涉，这也是该模型的缺点之一。

Cook-Torrance方程推导

直接光照中镜面光照的BRDF可以用Cook-Torrance方程描述：

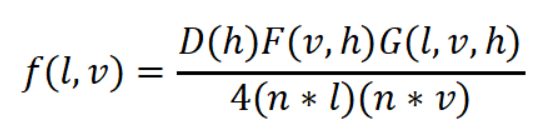
其中D(h)为法线分布函数，输入向量h返回法线为h的微平观面占宏观平面的比例。F(v,h)为菲涅尔系数，返回不同出射角下折射与反射的比例系数。G(l,v,h)为几何遮蔽函数，计算光线在微平面反射时被其他不规则微平面遮蔽的系数，以此来满足方程的能量守恒。

该方程由辐射度学公式推导而来，对于某个物体某个平面上的一个面积A，光照照射过来的辐射通量为φ，则该面积A上的辐照度（Irradiance）为：

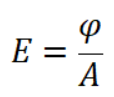
假设光照入射方向与该点法线的夹角为θ(n·l)，存在该面积A的单位半球朝向入射方向上的立体角ωi的辐亮度（Radiance）为：

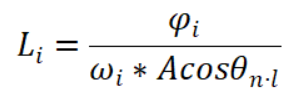
该方程可以写成微分形式，则入射的辐亮度L可以看成关于面积为微元A点p在入射方向微元立体角ωi方向上辐亮度的二阶导数：

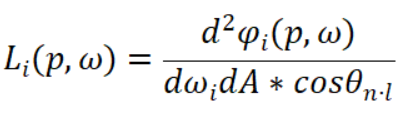
由此可以知道入射时的辐亮度和辐照度的关系：

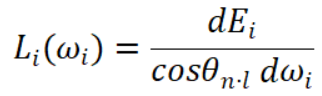
同时,由于在镜面光照中仅有微观下法线为h的微平面参与了反射计算,设该方向的立体角为ωh,可以用法线分布函数D(h)函数描述微观状态下的dA，也就是法线方向为h的微表面微元面积，该值等于一个二阶导数：

联立可以知道入射的辐射通量为：

由于引入了微平面法线ωh，原来的宏观法线n与入射光线l夹角改为了微观法线h与入射光线l的夹角。此时我们已知入射的辐射通量可以得出出射的辐射通量，从入射到出射，这个过程中受到了几何遮蔽函数G和菲涅尔系数F的损失，有：

最终，已知入射的辐射通量Irradiance，可以得出出射的辐亮度radiance：

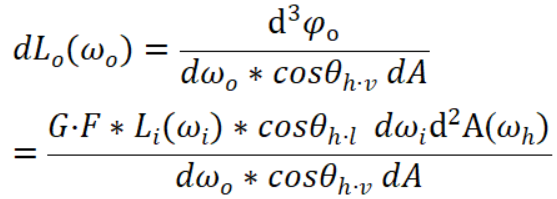
在前文说过，BRDF为出射辐亮度与入射辐照度的比值，由此可以列出公式：

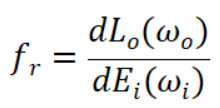
我们在上文推导出来了这两个分量，结合起来计算BRDF：

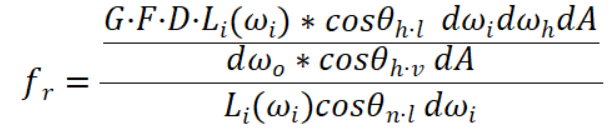
经过约分，可以得出Cook-Terrance方程的大概外形：

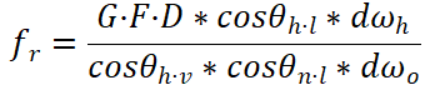
既然h为l与v的半向量，则h与l的夹角等价于h与v的夹角，二者是一样的。那么，化简BRDF的关键因素就是立体角微元dωh与dωo的比值了，该值可以用下图的关系推导出来：

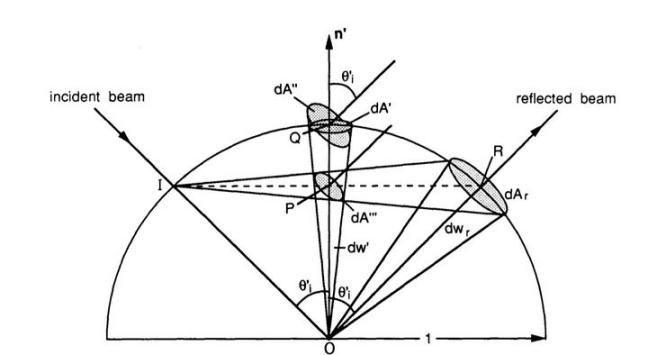
最终，立体角微元dωh与dωo的比值关系为：

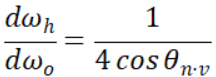
其中，θn·l为入射角与法线的夹角，同时也等价于出射角与法线的夹角。将该关系代入上式，可以得出最终的Cook-TerenceBRDF中的Specular项：

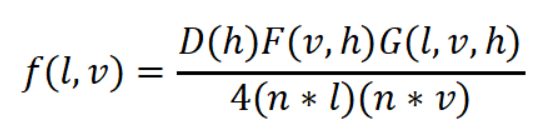
菲涅尔系数

与Blinn-Phong模型中不同，对于绝缘体中常常存在菲涅尔反射，它表示了该介质反射光的比例。菲涅尔系数的值取决于入射光线与物体法线的夹角和介质的折射率。并且由于介质的折射率可能随光谱的变化而变化，菲涅尔系数为一个光谱量。在微小面理论中，我们处理的不是光滑的表面，而是局部光滑的微观几何。在这种情况下，我们关注的是单个表面点的菲涅尔反射率。由于贡献BRDF的表面点都有微观几何法线等于半向量h，因此h是应该用于计算菲涅耳系数的向量。

对于一个介质而言其反射系数常常被认为是一个介质表面镜面的反射率，该值在由0到1之间的sRGB值组成。在运算中将该值称为曲面的镜面颜色，是计算菲涅尔反射率的理想参数，原始的菲涅尔方程十分复杂，Schlick给出了一个菲涅尔方程的近似方程，能够廉价而准确的计算出菲涅尔系数的近似值：

其中F0即为介质的菲涅尔系数。这个方程广泛地用于计算机图形学中，并且在BRDF中将微表面法线h代替了上式中的宏观法线n。

法线分布函数

大多数表面的微观几何形状并不是均匀分布。大部分微平面法线分别指向“纵向”（即接近宏观表面法线n），而不是“横向”（远离宏观法线n）。微表面法向量的统计分布是通过微观几何的法线分布函数D(m)来定义的。与菲涅尔系数不同的是，法线分布函数的值不被限制在0和1之间——虽然值必须是非负的，但允许可以任意大，此时代表法线指向特定方向的微表面的比例非常高。此外，与菲涅尔系数不同的是，法线分布函数既不是光谱值，也不是RGB值，而是标量值。在微面BRDF术语中，法线分布函数评估方向h，以确定微平面中法线为h的微平面占总平面的比例。这就是为什么在Cook-Terrance的BRDF模型中在需要乘以法线分布函数。法线分布函数决定了镜面高光部分的大小、亮度和形状。

几何遮蔽函数

几何函数是保证微平面的BRDF理论上能量守恒，逻辑上自洽的重要一环。其描述了微平面自阴影的属性，表示具有半矢量法线的微平面中，同时被入射方向和反射方向可见，即没有被遮挡的光线的比例。单纯的法线分布函数得到数值不是有效的微表面的法线强度，需结合几何函数，才能得到有效入射和出射法线，进而得到能对BRDF产生贡献的强度。如下图，比较了一个随机的微小平面被某一平面观察到后有无几何遮蔽函数是否满足了能量守恒原则。

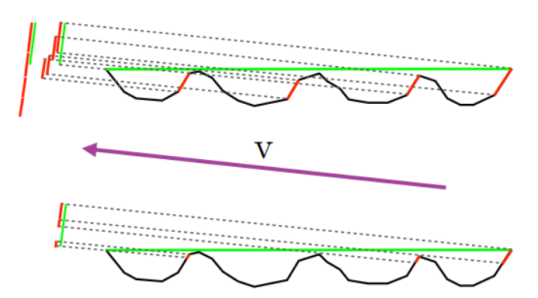
如上图，用红色标记的表面区域为法线为h的微小平面，也是在镜面计算中起作用的平面。宏观表面积（二维侧图中的长度）对视图方向（v方向）的投影显示在左上方的绿色线（视图方向本身由图中间的紫色箭头表示）。单个红色表面区域的投影区域显示为单独的红线，在上图的左上角我们可以看到，将它们相加后，活动微观几何区域（长红线）的投影大于宏观区域的投影（绿线）。这是不合逻辑的，将导致致BRDF反射比它接收到的更多的能量，违背了能量守恒原则。而在下图在底部的红线只显示了活动表面区域的可见部分。主动微观几何区域的投影现在小于宏观区域的投影，这种情况才是正确的。当视角较低时，这种影响将会更加明显。

几何函数与法线分布函数的联系

几何函数的解析形式的确认依赖于法线分布函数。在微平面理论中，通过可见微平面的投影面积之和等于宏观表面的投影面积的恒等式，选定法线分布函数，并选定几何函数的模型，就可以唯一确认几何函数的准确形式。在选定几何函数的模型后，几何函数的解析形式的确认则由对应的法线分布函数决定。

法线分布函数需要结合几何函数，得到有效的法线分布强度。 单纯的法线分布函数的输出值并不是能产生有效反射的法线强度，因为光线的入射和出射会被微平面部分遮挡，即并不是所有朝向m=h的微表面，能在给定光照方向l和观察方向V时可以顺利完成有效的反射。几何函数即是对能顺利完成入射和出射的微平面概率进行建模的函数。法线分布函数需要结合几何函数，得到最终对BRDF能产生贡献的有效法线分布强度。

附录：法线分布函数与几何遮蔽函数的发展与比较

在这里感觉自己只是对目前常用的D和G做了一次简单的总结，如果看完整的D和G概述，非常推荐毛星云老师的博客，令人受益匪浅。

在使用Cook-Terrance模型对物体表面进行着色时，需要对法线分布函数和几何遮蔽函数做出适当的选择。

常见的法线分布函数

业界提出过的法线分布函数有数十种，其中应用得最广泛的是BeckMann分布，Phong分布和Trowbridge-Reitz 分布（即GGX分布），下面将介绍这些分布的不同。

Beckmann分布

Beckmann分布起源于针对微表面的高斯粗糙度假设，于1963年提出，在光学中被广泛应用。也是Cook-Terrance模型在提出时应用的分布函数。

其中，α为物体表面的粗糙度，n为物体表面的宏观法线方向，m为物体表面的微观法线方向。

Blinn-Phong分布

Blinn-Phong起源于Phong的经验模型，由Blinn于1977年给出，作为（非基于物理的）Phong着色模型的改进，以更好地拟合微平面BRDF的结构。Blinn在提出Blinn-Phong分布时没有指定归一化因子，但是由于法线分布函数遵循一条规律，即将法线为m微平面映射到宏平面时，法线m在以宏观表面的法线n为轴的半球上映射的积分为宏平面的面积。有公式为：

根据这个公式可以推导出Blinn-Phong法线分布函数：

幂α为物体表面粗糙度参数，高值表示光滑表面，低值表示粗糙表面。对于非常光滑的曲面，值可以任意高（一个完美的镜面α=∞），并且通过将设置为0可以实现最大随机曲面（即漫反射表面）。

GGX分布

GGX即Trowbridge-Reitz分布，最初由Trowbridge和Reitz 于1975年的论文推导出，在Blinn 于1977年的论文中也有推荐此分布函数，但一直没有受到图形学界的太多关注。30多年后，

Trowbridge-Reitz分布被Walter等人独立重新发现并发表在2007年的论文中，并将其命名为GGX分布。在GGX分布被重新发现并提出之后，开始在电影和游戏行业中广泛传播与应用，成为了如今游戏行业和电影行业中最常用的法线分布函数。GGX的分布函数如下所示：

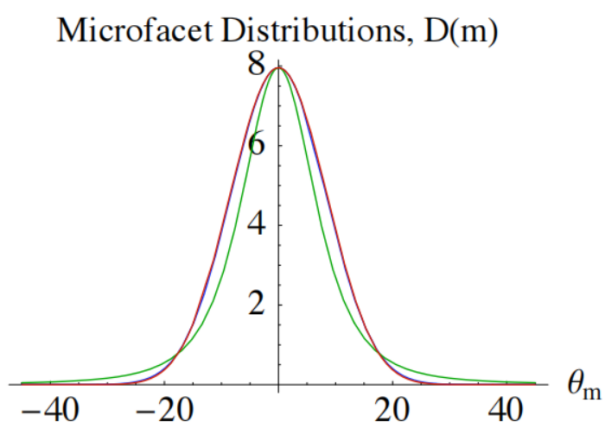
GGX相较于Beckmann分布和Blinn-Phong分布有更长的拖尾，如下图，表达了三个法线分布函数关于微观法线与宏观法线夹角关系的图像：

 这种拖尾在以往只能靠多个BRDF拟合才能做到。这也是GGX在业界流行的原因。

常见的几何遮蔽函数

在镜面BRDF的D,G,F三项中，如果说法线分布函数是最核心的一项，那么几何函数则是核心的辅助项，而且是三项中最复杂的一项。

Smith遮蔽函数

最初的几何遮蔽函数由Smith于1967提出，也是现在业界所采用的主流遮蔽函数，Eric Heitz在2014年将其拓展为Smith联合遮蔽阴影函数。

几何函数具有两种主要形式：G1和G2，其中：G1为微平面在单个方向（光照方向L或观察方向V）上可见比例，一般代表遮蔽函数或阴影函数。G2为微平面在光照方向L和观察方向V两个方向上可见比例，一般代表联合遮蔽阴影函数。在实践中，G2由G1推导而来。

 其中,χ+(x)表示正特征函数：

 而生剩余的1/(1+Λ(ν))则是Smith遮蔽函数的广义形式 ，表示为表面斜率上的积分：

其中，θ0为微平面法线与宏平面法线的夹角，P22(xm,ym)为微表面的斜率分布，m表示与法线相关的斜率。而P22(xm,ym)与法线分布有关系：

 从上文中的式子可知，在几何遮蔽函数的实际应用中，常根据法线分布函数选取对应的几何遮蔽函数。

Smith联合遮蔽阴影函数

除了G1之外，业界常常使用Eric Heitz在[Heitz 2014]中提出的Smith联合遮蔽阴影函数G2(l, v, m)来代替遮蔽函数G1(m, v)。联合遮蔽阴影函数具有多种形式，最简单的即为分离的遮蔽阴影函数，由Walter于2007年提出，在这种情况下光线照到微平面的阴影与人眼观察到的遮蔽是独立计算的，其结果为二者的相乘，所以该方法不考虑遮蔽与阴影之间的相关性：

为了更加精确的计算遮蔽与阴影的关系，[Ross et al. 2005]提出了与高度相关的遮蔽阴影函数，模拟了由于微表面高度引起的遮蔽和阴影之间的相关性。微平面相对于微表面升高的越多，对于出射方向未被遮蔽和入射方向未被掩蔽的可见概率会同时增加。 因此，遮蔽和阴影通过微平面的升高而相关。 这种相关性以联合遮蔽阴影函数的高度相关形式进行表达：

需要注意的是，当出射方向和入射方向彼此远离时，此形式是准确的，但是当方向接近时，此形式会估算出更多的阴影。Heitz建议在实践中使用此版本的遮蔽阴影函数，因为它比可分离的遮蔽阴影函数更精确，却同时具有相同的计算复杂度。

根据法线分布函数确定遮蔽函数

在确定了选用的法线分布函数后，可以根据上文中的公式确定对应的几何遮蔽函数，BeckMann分布的Λ函数为：

而对于Blinn-Phong分布而言，该函数不具备形状不变性，所以不存在Λ函数，Walter的文章中建议使用BeckMann的Λ函数。

对于GGX分布而言，其Smith遮蔽函数对应的Λ解析形式相对简单：

其中为α物体的粗糙度参数，θ0为微平面法线与宏平面法线夹角。

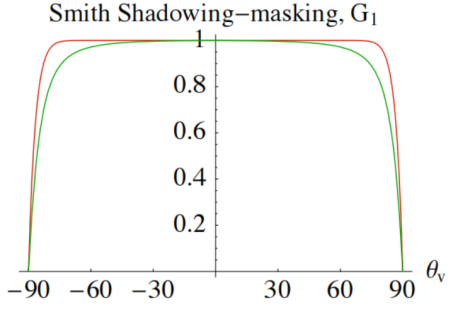
几何遮蔽函数的返回值处于[0,1]之间，而且在粗糙度α较低时接近1。同样的，GGX分布的几何遮蔽函数图像的拖尾也要长于Beckmann分布的几何遮蔽图像。如下图：

根据上文中Cook-Terrance BRDF模型，可以在根据在空间中的光照方向、每个像素的表面法线方向、视角观察方向和指定的粗糙度和金属度起来得到正确的直接光照的物理渲染结果。但是在光栅化中显然不能直接对每个像素直接计算其积分结果，需要将场景中的主光源和其他环境光照区分，主光源直接代入上文中写好的Diffuse和Specular公式即可，简单地写成Shader如下：

Shader "Hidden/BRDF_DirectLight"
{Properties{_MainTex ("Texture", 2D) = "white" {}_MainColor("MainColor",Color)=(1,1,1,1)_SmoothNess("SmoothNess",Range(0.01,0.975))=1.0_MatalNess("MatalNess",Range(0.01,1.0))=1.0_FernelSize("FernelSize",Range(0.0,1.0))=1.0_IndirectDiffuseValue("IndirectAiffuseValue",Range(0.0,1.0))=0.5_DiffuseRatio("DiffuseRatio",Range(1.0,2.0))=1.0_SpecularRatio("SpecularRatio",Range(1.0,20.0))=1.0}SubShader{Pass{CGPROGRAM#pragma vertex vert#pragma fragment frag#include "UnityCG.cginc"float _SmoothNess;float _MatalNess;sampler2D _MainTex;float4 _MainTex_ST;float4 _MainColor;float _IndirectDiffuseValue;float _DiffuseRatio;float _SpecularRatio;struct VertexData{float4 vertex:POSITION;float3 normal:NORMAL;float2 uv:TEXCOORD0;};struct VertexToFragment{float4 pos:SV_POSITION;float3 normal:TEXCOORD0;float3 worldPos:TEXCOORD1;float2 uv:TEXCOORD2;};float DisneyDiffuse(float3 worldNormal,float3 worldViewDir,float3 worldLight,float3 halfDir,float roughness){float PI=3.14159265;float cosLightNormal=saturate(dot(worldLight,worldNormal));float cosViewNormal=saturate(dot(worldViewDir,worldNormal));float cosViewHalf=saturate(dot(halfDir,worldLight));float F90=0.5+2*roughness*cosViewHalf*cosViewHalf;float FdV=1+(F90-1)*pow(1-cosViewNormal,5);float FdL=1+(F90-1)*pow(1-cosLightNormal,5);return FdL*FdV/PI;}//标准GGX法线分布float GGXDistribution(float3 worldNormal,float3 halfDir,float a){float PI=3.14159265;a=a*a;float cosAngle=max(0,dot(worldNormal,halfDir));float x=cosAngle*cosAngle*(a*a-1)+1;x=x*x*PI;return a*a/x;}//几何函数Gfloat GeometrySchlickGGX(float NdotV, float roughness){float r = (roughness + 1.0);float k = (r*r) / 8.0;float num = NdotV;float denom = NdotV * (1.0 - k) + k;return num / denom;}float GeometrySmith(float3 N, float3 V, float3 L, float roughness){float NdotV = max(0,dot(N, V));float NdotL = max(0,dot(N, L));float ggx2 = GeometrySchlickGGX(NdotV, roughness);float ggx1 = GeometrySchlickGGX(NdotL, roughness);return ggx1 * ggx2;}float G_SchlicksmithGGX(float3 worldNormal,float3 view,float3 light, float roughness){float dotNL=saturate(dot(worldNormal,light));float dotNV=saturate(dot(worldNormal,view));float r = (roughness + 1.0);float k = (r*r) / 8.0;float GL = dotNL / (dotNL * (1.0 - k) + k);float GV = dotNV / (dotNV * (1.0 - k) + k);return GL * GV;}VertexToFragment vert(VertexData v){VertexToFragment VToF;VToF.pos=UnityObjectToClipPos(v.vertex);VToF.normal=UnityObjectToWorldNormal(v.normal);VToF.worldPos=mul(unity_ObjectToWorld,v.vertex);VToF.uv=TRANSFORM_TEX(v.uv,_MainTex);return VToF;}fixed4 frag(VertexToFragment VToF):SV_TARGET{float PI=3.14159265;fixed3 worldLight=normalize(UnityWorldSpaceLightDir(VToF.worldPos));fixed3 worldViewDir=normalize(_WorldSpaceCameraPos-VToF.worldPos);fixed3 worldNormal=normalize(VToF.normal);fixed3 halfDir=normalize(worldLight+worldViewDir);float RoughNess=1-_SmoothNess;fixed3 TexColor=tex2D(_MainTex,VToF.uv).rgb*_MainColor.rgb;//fixed3 Lambert=0.5*saturate(dot(worldNormal,worldLight))+0.5;fixed3 DiffusBRDF=DisneyDiffuse(worldNormal,worldViewDir,worldLight,halfDir,RoughNess)*_DiffuseRatio;//fixed3 DiffusBRDF=TexColor/PI;//漫反射的BRDF系数,这里采用Disney的漫反射着色公式float getNDF=GGXDistribution(worldNormal,halfDir,RoughNess);//法线分布系数float getMSF=G_SchlicksmithGGX(worldNormal,worldViewDir,worldLight,RoughNess);//几何遮蔽函数float3 frenelScale=lerp(fixed3(0.04,0.04,0.04),TexColor,_MatalNess);fixed3 Fernel=frenelScale+(1-frenelScale)*pow(1-max(0,dot(halfDir,worldViewDir)),5);//菲涅尔系数，同时也是高光反射的BRDF权重float3 DiffuseImprotance=(1-Fernel)*(1-_MatalNess);//漫反射BRDF的权重float3 SpecularBRDF=Fernel*getNDF*getMSF/max(0.01,4*dot(worldLight,worldNormal)*dot(worldViewDir,worldNormal))*_SpecularRatio;//高光BRDFreturn fixed4((DiffuseImprotance*(DiffusBRDF+_IndirectDiffuseValue)*TexColor+SpecularBRDF)*dot(worldLight,worldNormal),1.0);}ENDCG}}
}

在实际应用中对于某一直接照射到物体表面的光源（往往是方向光源）而言，仅仅计算从该方向照射过来的光照即可。我们将金属度和粗糙度在[0,1]之间插值，设置颜色为蓝色，得到100个小球的渲染结果：

需要注意的是，上文中金属度较高的物体呈现黑色，因为这仅仅是直接光照下的BRDF，并没有对周遭环境的捕捉。在现实世界中一个物体的真实着色情况还需要考虑间接光照对物体的着色情况带来的影响，即环境中其他物体折射到物体的光照或者是其他的自发光光源带来的光照，这些光照效果也称为全局光照。在光栅化的渲染流程中可以引入基于图像照明技术(IBL，Image Based Lighting)来计算环境光照对物体的漫反射和镜面反射结果，其原理仍然是光照方程的简单扩展应用。在下文中我们进行叙述。

光栅化下的环境光照IBL

基于图像照明技术Image Based Lighting，顾名思义，就是将当前物体环境下的光照结果进行预计算后，在光栅化下进行实时采样的过程。上文中实际上一个像素点的光照计算，本质上是一个积分，我们计算直接光照就是仅仅执行某一个方向微元上的未积分的结果，那么预计算本质上是将当前物体所处环境贴图预积分，然后在实时渲染中采样该积分即可，在本文章中并不会计算预积分贴图，详情请看上一篇博客（发早了，这一篇理论上是上一篇的铺垫）。因为在unity中，预积分后的环境贴图已经提前算好了，并不需要我们自己插手计算，在本文中我们专注于采样结果即可，在下一篇文章中，我将简单论述Unity中的预积分技术（不包括次表面散射的预积分贴图）。首先对于上文中的BRDF与Radiance的积分，存在拆分近似：

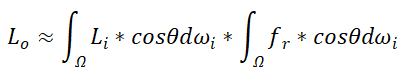
对于左边在球面上入射光的Irradiance，这一部分一般在软件内预卷积完成了。而有右边的积分才是我们需要主要计算的积分项。对于该积分项肯定不能在实时中计算，我们已知将会使用法线分布函数和几何遮蔽函数的逻辑，那么将这个积分也预计算然后实时采样肯定才是最好的。预计算该积分唯一的变数就是里面的三个变量：法线与出射角夹角，物体的表面粗糙度，还有菲涅尔的折射率F0（入射角ωi则是积分的主角）。如果将三个变量都根据值的组合做成贴图，那么需要一个Cube或者其他的一些保存方式，这肯定是一个复杂的过程和开销。如果能仅预计算两个变量，那么我们在实时采样时仅需要采样一张二维贴图就好了。而现实中往往也是将菲涅尔的折射率F0从积分中拆出来，这需要一些数学运算：

将菲涅尔项展开，我们可以将F0从积分中拆开，变成两个积分项：

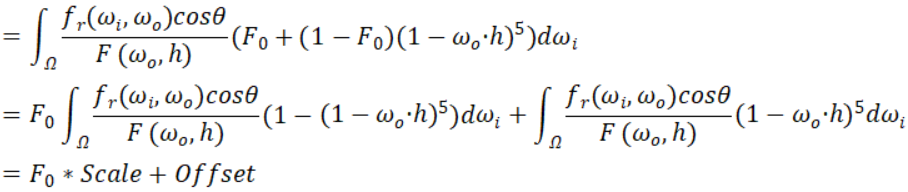
这样F0就从积分中拆了出来，将原本的BRDF积分变成了两个部分，两个部分仅有一些加减法上的不同，我们可以将法线与出射夹角、粗糙度分别组合计算，计算结果保存为二维贴图，然后与预积分的Irradiance相乘，就能算出光栅化下的环境光照。

假设现在我们已经得到了预积分贴图，那么我们实际上只需要采样即可了，我们在采样时并不知道此时的预积分贴图长什么颜色，所以默认都是白色的。采样的重点则放在了1件事情上：计算上文中这两个积分。

在代码中算积分乍一看无疑是一个难题，这使我们不得不使用蒙特卡洛积分形式来代表我们的积分：

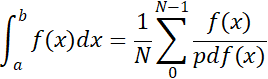
其中，N为求积分所使用的样本数，而pdf为生成[a,b]内样本x的概率密度函数，描述一个特定样本在样本集中出现的概率。在这里不会对蒙特卡洛积分进行详述，我们需要知道的是，样本越多肯定意味着计算结果越近似于积分结果，但是可能会造成较大的方差。当样本概率密度与目标函数越接近，积分的方差越小。这使得我们常常利用目标函数来反推概率密度函数，因为这样计算结果最接近原积分计算结果。这在下文中会有所体现。

我们的渲染方程使用蒙特卡洛积分的方法写出即有： 

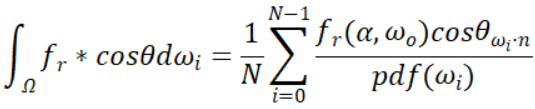
其中θ为光源与法线的夹角，光线出射角ωo和表面粗糙度α都可以看做已知的。那么计算该蒙特卡洛的重点就是如何获得ωi的样本。如果从半球上随机选出方向作为样本，我们可以假设一个球面坐标θ和φ，这两个轴分量就是我们的随机值，然后看起来将球面坐标转入笛卡尔坐标就可以得到一个随机样本了。

如果仅仅只是半球上的随机采样的话，对于纯Diffuse表面来说是堪用的（因为Diffuse的出射Radiance本来就是向四周均匀散射的）。对于Specular表面而言却是不合适的，这是由于Specular表面的粗糙度相较于Diffuse而言要小，这导致当一束Radiance射入表面时，受到微表面的粗糙度影响，光线折射的光瓣也与Diffuse表面不同：

光瓣的存在导致我们如果简单的在球面随机采样不可避免地采样到非光瓣方向的样本，那么这些样本会导致积分结果的方差加大，所以在光栅化采样时，所使用的样本需要拟合光瓣的方向来减少反差，蒙特卡洛积分中减少方差的方法很多，其主要思想为重要性采样重要性采样，利用与被积函数相似的概率密度函数生成样本，以最小地减少方差。例如我们上文中的被积函数为BRDF与cosθ的乘法，它对应的概率密度函数为：

其中θh为法线与halfDir的夹角。注意这里是生成HalfDir样本所用的概率密度函数，而生成ωi样本的概率密度函数为：

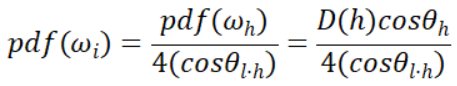
将该概率密度函数函数代入到上文中的积分，可以将蒙特卡洛积分的形式简化：

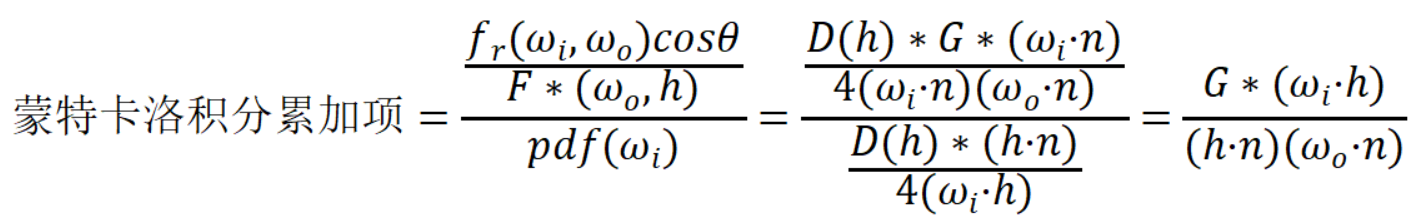
该方程为实际上在预计算时最终应用的方程式。同时，在实际应用中，往往使用生成ωh样本的概率密度函数来获得样本，这是由于该概率密度函数实现了球面积分上的归一化而选取的：

这个公式我在当时总结了一句话： 每个微平面在ω方向投影的和是宏观平面在ω方向上的投影，这里的ω可以是任意方向。本质上无非就是一个表面的微表面法线处在表面法线所在的半球中，这些微表面面积在表面的投影的和一定等于表面面积，所以这里为1是非常合理的（亏我还费劲证明了好半天，有点低能了）。同样的原理有如下关系： 

同样的，当我们获得ωh后，需要进行一些简单的操作来得到ωi方向，这一逻辑将在代码中有所体现。

根据这个思想来求解蒙特卡洛积分的方法有积累密度分布函数CDF反演采样法，接受-拒绝采样，Meropolis采样，马尔科夫蒙特卡洛采样，重要性重采样等方法。在本文中仅使用了CDF反演法来获得样本（这是最常见的一种）。这个方法概述如下：

1. 获得[0,1]分布内的两个均匀分布随机数（因为球面坐标有两个分量），这一点由低差异序列方法获得。
2. 计算目标的积累分布函数，即将目标概率分布pdf在球面坐标的两个作用域上进行积分得到积累分布函数cdf。
3. 将积累分布函数取反，代入随机分布函数，得到符合目标概率分布的随机样本。

这个过程并不会在本文中再运算一遍，因为网络上关于运算过程的解析已经很多了，比如tomeng大神的这篇文章，我这里直接贴出运算结果，首先对于GGX的法线分布，目标概率分布为（sinθ是由于球面积分的缘故）：

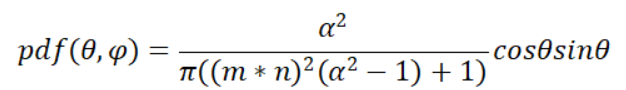
那么对于目标概率分布中关于θ的边际概率密度为：

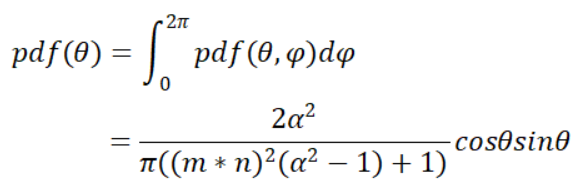
 由此可以得出φ的条件概率密度：

 将边际概率密度积分，算出积累分布函数，取反。最终可以算出符合概率密度分布的随机样本：

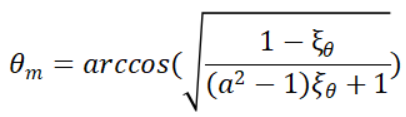
其中，ξθ和ξφ代表θ轴和φ轴的[0,1]内的随机数，当我们通过这两个轴构建球面向量样本后，还需要将样本从顶点空间转移到世界空间（实测不转移也不会有什么问题）。就能得到积分所需要的样本。

在光栅化下的预计算中，常常使用低差异序列来生成随机数：

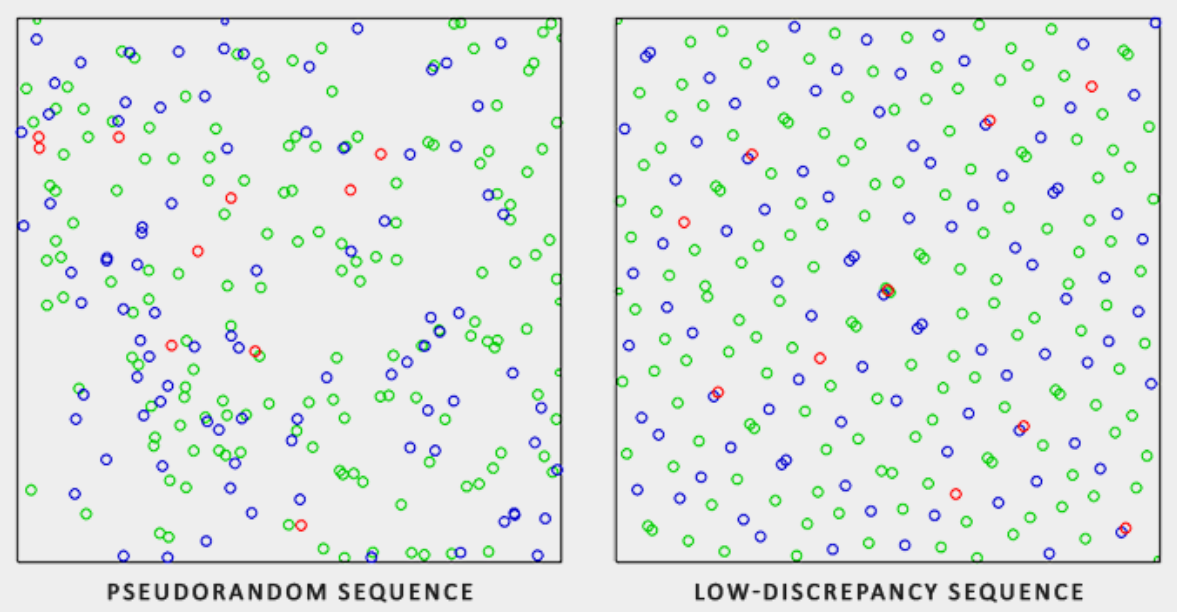
低差异序列

使用伪随机数产生随机采样会造成方向分布不均匀，因为伪随机数之间并不了解彼此的信息，可能会产生丛聚，这会导致蒙特卡罗积分方程式中，预估的准确性较差，收敛速度慢。通过使用低差异序列替换伪随机数，我们可以提高准确度，它本质上可以更好地保证分配的方向。使用Low-Discrepancy Sequence来生成蒙特卡罗采样向量，这个过程被称为Quasi-Monte Carlo准蒙特卡洛积分。Quasi-Monte Carlo方法有更快的收敛速度，使他能够胜任大型复杂的应用。

 论述这个概念并不是本文的重点，我作为记录将代码写在这里：

            float RadicalInverse_VdC(uint bits){bits = (bits << 16u) | (bits >> 16u);bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);return float(bits) * 2.3283064365386963e-10; // / 0x100000000}float2 Hammersley(uint i,uint n){return float2(float(i)/float(n),RadicalInverse_VdC(i));}

但是在其他情况下，例如自己写的路径追踪渲染器或者是其他的一些渲染逻辑中，用其他方法生成的随机数也是能够胜任生成随机坐标的任务的。

既然已经可以得出入射光线的样本，我们令图片二维坐标的U=法线与出射角的夹角，V=粗糙度，即UV作为积分的输入组合（这是由于这两个变量正好和UV一样都处于0到1之间），通过随机数生成入射光线的样本，进而预计算积分贴图即可：

Shader "Hidden/IBLShader"
{ SubShader{// No culling or depthCull Off ZWrite Off ZTest AlwaysPass{CGPROGRAM#pragma vertex vert#pragma fragment frag#include "UnityCG.cginc"struct appdata{float4 vertex : POSITION;float2 uv : TEXCOORD0;};struct v2f{float2 uv : TEXCOORD0;float4 vertex : SV_POSITION;};v2f vert (appdata v){v2f o;o.vertex = UnityObjectToClipPos(v.vertex);o.uv = v.uv;return o;}//使用低差异序列，使得蒙特卡洛积分在采样时的点更加均匀//输入为当前的序列i和总序列n，返回1/n和随机均匀分布的i(即φ和θ)float RadicalInverse_VdC(uint bits){bits = (bits << 16u) | (bits >> 16u);bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);return float(bits) * 2.3283064365386963e-10; // / 0x100000000}float2 Hammersley(uint i,uint n){return float2(float(i)/float(n),RadicalInverse_VdC(i));}float3 ImprotanceSampleGGX(float2 angle,float roughNess){//关于GGX的重要性采样，其中angle的x分量为球面的横夹角φ，y分量为球面纵夹角θfloat a=roughNess*roughNess;//根据迪士尼的原始 PBR 研究，Epic Games 使用平方粗糙度来获得更好的视觉效果float FIi=2*UNITY_PI*angle.x;//得到φ的PDF值//根据θ的cdf公式，得到θ的sin和cos值float getCos=sqrt((1-angle.y)/(1+(a-1)*angle.y));//这里不要忘了有一个+1的操作float getSin=sqrt(1-getCos*getCos);//根据φ与θ的值得球面坐标在笛卡尔坐标系下的表示方法（球的半径为1）float3 halfDir;halfDir.x=getSin*cos(FIi);halfDir.y=getSin*sin(FIi);halfDir.z=getCos;return halfDir;//返回切线空间中的HalfDir}//上文中的GGX得到的是每个像素的法线空间中的halfDir//所以我们需要做和法线采样同样的操作：将向量从法线空间转入世界空间float3x3 GetTangentMatrix(float3 tangentZ){float3 up=abs(tangentZ.z)<0.999?float3(0,0,1):float3(1,0,0);float3 tangentX=normalize(cross(up,tangentZ));float3 tangentY=cross(tangentZ,tangentX);return float3x3(tangentX,tangentY,tangentZ);//返回的是三个基轴的行矩阵}float3 TanegntToWorld(float3 vec,float3 tangentZ){return mul(vec,GetTangentMatrix(tangentZ));}float3 Smith_WalterBeckmanGeometric(float roughness,float NdotV,float NdotL){float roughnessSqr = roughness*roughness;float NdotLSqr = NdotL*NdotL;float NdotVSqr = NdotV*NdotV;float calulationL = (NdotL)/(roughnessSqr*sqrt(1- NdotLSqr));float calulationV = (NdotV)/(roughnessSqr*sqrt(1- NdotVSqr));float SmithL = calulationL < 1.6 ? (((3.535 * calulationL) + (2.181 * calulationL * calulationL))/(1 + (2.276 * calulationL) + (2.577 * calulationL * calulationL))) : 1.0;float SmithV = calulationV < 1.6 ? (((3.535 * calulationV) + (2.181 * calulationV * calulationV))/(1 + (2.276 * calulationV) + (2.577 * calulationV * calulationV))) : 1.0;float Gs =  (SmithL * SmithV);return Gs;}float GeometrySchlickGGX(float NdotV, float roughness){float a = roughness;float k = (a * a) / 2.0;float nom   = NdotV;float denom = NdotV * (1.0 - k) + k;return nom / denom;}float GeometrySmith(float3 N, float3 V, float3 L, float roughness){float NdotV = max(dot(N, V), 0.0);float NdotL = max(dot(N, L), 0.0);float ggx2 = GeometrySchlickGGX(NdotV, roughness);float ggx1 = GeometrySchlickGGX(NdotL, roughness);return ggx1 * ggx2;}//如果我们假设每个方向的入射辐射都是完全白色的（因此L(p,x)=1.0,表示为不考虑CubeMap颜色影响）//我们可以预先计算BRDF的响应，给定输入粗糙度和法线之间的输入角度n和光方向ωi，或n⋅ωi，获得在贴图中对应的积分结果float2 CaculateSummaryBRDF(float NdotV,float roughNess){int SampleCount=1024;float3 normalDir=float3(0,0,1);float3 viewDir;viewDir.x=sqrt(1-NdotV*NdotV);//x为sinθviewDir.y=0;viewDir.z=NdotV;//z分量为cosθ//从这个逻辑可以看出，viewDir是处于XZ平面中矢量//其值可以用几何关系(即θ角和n的模长为1这两个已知条件)推导出来float scale=0;float bias=0;for(int i=0;i0){float vis=(GeometrySmith(normalDir,viewDir,LightDir,roughNess)*VdotH)/(NdotH*NdotV);float FrenelScale=pow(1-VdotH,5);scale+=(1-FrenelScale)*vis;bias+=FrenelScale*vis;}}scale/=float(SampleCount);bias/=float(SampleCount);return float2(scale,bias);}fixed4 frag (v2f i) : SV_Target{return float4(CaculateSummaryBRDF(i.uv.x,i.uv.y),0,1);}ENDCG}}
}

使用这个Shader可以输出上文中积分的预计算结果：

 这个贴图用于在实时渲染中利用法线和出射向量的夹角和粗糙度这两个分量作为采样坐标进行采样得到两个积分的计算结果，然后和公式中写的一样，将A项乘以菲涅尔的反射率，再与IrradianceMap相乘，就能得到当前环境的积分计算的近似结果：

                //UNITY_SPECCUBE_LOD_STEPS是定义在UnityImageBaseLight.cginc里的常量//Unity会为环境贴图生成不同层级的mipmap，0-5级从模糊到清晰，所以UNITY_SPECCUBE_LOD_STEPS默认定义为6,此值为感性粗糙度和立方体贴图mipmap层级之间的系数。float mip=RoughNess*UNITY_SPECCUBE_LOD_STEPS;//根据粗糙度读取不同层级的mipmapfloat3 R=reflect(-worldViewDir,worldNormal);//不要错误地理解了反射的意义，这里得到的值是ViewDir的反射，而不是入射光线的反向量，这也是读取cubeMap的基础操作//UNITY_SAMPLE_TEXCUBE_LOD根据反射向量和mipmap层级对立方体纹理贴图进行采样，采样的纹理是一个HDR值float4 rgbm=UNITY_SAMPLE_TEXCUBE_LOD(unity_SpecCube0,R,mip);//上文中求出来的有可能是一个HDR值，而通过对该值的解码(即下文中的这一行操作)得到正确的环境贴图的采样值float3 preColor=DecodeHDR(rgbm,unity_SpecCube0_HDR);//最终获得准确的CubeMap颜色float NdotV=saturate(dot(worldNormal,worldViewDir));float2 TexSpecular=tex2D(_SapecularIBLTex,float2(lerp(0,0.99,NdotV),lerp(0,0.99,1-_SmoothNess))).rg;//BRDF积分贴图保存的是某一cosθ和roughness组合的BRDF的预计算好了的积分值//其中R通道保存为cosθ对应的V0*(1-Fc)，G通道保存为roughNess对应的V0*Fc（Fc为（1-cosθ）的五次方，这里只是为了加速计算的一个trick）//所以在采样时要依照这两个参数对贴图进行采样float3 IBLSpecular=preColor*(Fernel*TexSpecular.x+TexSpecular.y);

同时关于Diffuse也存在预积分方法，Unity中是通过三阶球谐函数实现的，这一点在另一篇博客有详细描述：

                //IBL高光项的球谐函数版本（仅用于测试）float3 irradiance=ShadeSH9(float4(worldNormal,1));float3 ambient=UNITY_LIGHTMODEL_AMBIENT;float3 IBLdiffuse=max(float3(0,0,0),ambient+irradiance)*TexColor;

最终将算出来的SpecularColor与原本的直接光照的BRDF相加就能得到正确的运算结果：

                returnColor+=float4((DiffuseImprotance*IBLdiffuse+IBLSpecular),1);

和直接光照一样，在这里放入示例图：

关于重要性采样的一些想法（仅代表个人发一些牢骚）：

如果我们直接去百度搜索关键词：重要性采样，我们一定能够得到这样的概念概述：
重要性采样是一种通过改变采样分布来提高采样效率的方法。它的核心思想是，如果我们知道被积函数在某个区间上的取值比在其他区间上更重要(即对积分结果的贡献更大)，那么我们可以选择在这个区间上更密集地采样，从而提高采样效率。

如果我们有一个目标概率分布p(ω)而言，我们可以用某一个简单的概率分布q(ω)来表示它：这个意思是，不仅要得到在p分布中生成ω的概率，也要得到在q分布中生成ω的概率。二者的概率比值将作为它在蒙特卡洛积分中的该样本的权重，这个权重即为该样本对于目标函数采样结果的贡献：

然后在蒙特卡洛积分中自然每次都需要乘以该样本对应的权重应用有：

这里看上去没什么问题，但是在图形学中我们使用重要性采样，情况有一些不同，这是由于在BRDF计算中，每次计算需要的样本数量都是1，我们在计算循环中每次仅需要对一条方向的光照溯源。上文中的多个样本，权重计算情况在这里并不合适。

并且，针对一个概率分布采样的方法并不止一个，例如接受-拒绝采样等。为什么会有一系列的采样方法，本质上是目标概率分布有时候并不会称心如意。例如，有时目标概率分布的积累分布并不可逆，有时目标概率本身是难以获得样本的。所幸在半球中获得指定目标概率的样本并不需要考虑这两种情况。我们这里使用重要性采样，并利用CDF反演法来获得符合分布的样本是合适的。我们可以将获得θ和φ的[0,1]随机数的情况看做是一个从简单分布q下获得样本的过程。而权重则是将该样本在复杂分布下计算其生成概率的结果。

当然根据不同的光照情况，重要性采样还有其他的扩展，例如重要性重采样，多重重要性采样计算启发式权重等，在这里暂时不做赘述。

参考文献 

LearnOpenGL - Specular IBL

非常优秀的一篇预计算的文章：基于物理的环境光渲染一 - 知乎

膜拜大神：深入理解 PBR/基于图像照明 (IBL) - 知乎