感知机预备知识

神经元

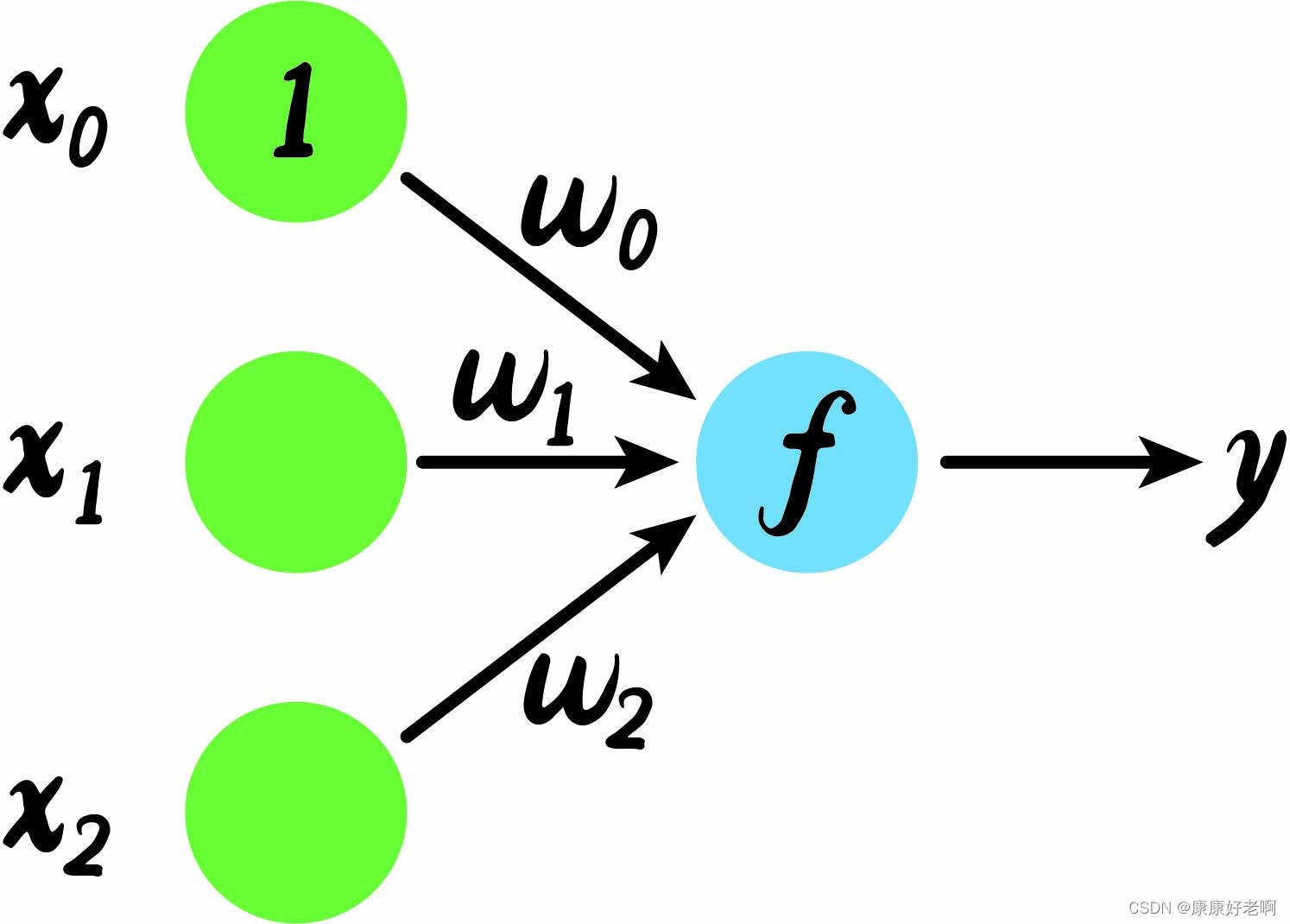
​ 感知机算法最初是由科学家从脑细胞的神经凸起联想而来。如下图，我们拥有三个初始xxx值，x1,x2,x0x_1,x_2,x_0x1​,x2​,x0​。其中x0=1x_0=1x0​=1为一个初始的常量，专业上称作“偏置”。每个xxx的值都会乘上一个权重值www，再线性组合生成一个多项式，这个多项式经过一个分类函数fff生成yyy。这个分类函数的作用就是将类别转化成0,10,10,1或者−1,1-1,1−1,1。绿色和蓝色的圆就像是一个个神经元，中间连接www就像是神经元用来传递信号的凸起。

数据集可分性

​ 从直观上理解，数据集可分的概念就是一个数据集可以通过一个超平面将不同的类别的数据样本点完全分开。

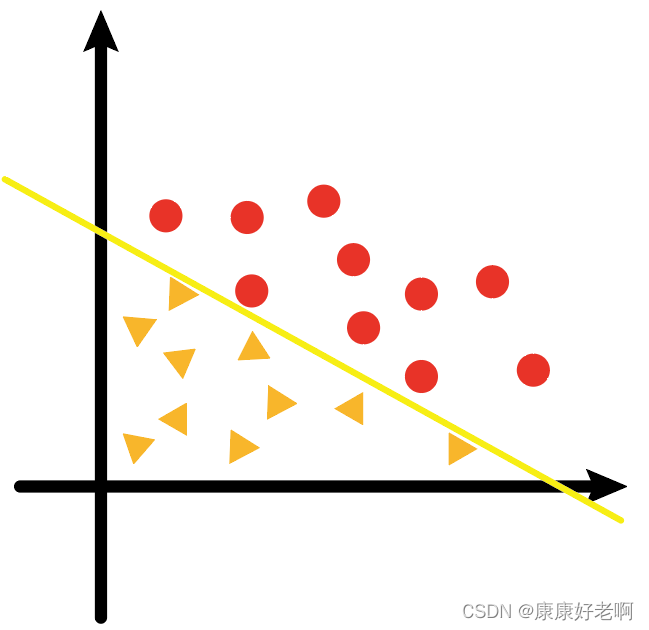
如上图，黄色的线可以将黄色三角形和红色圆形完全分开，不会有黄色三角形在红色圆形的区域，也不会有红色圆形在黄色三角形区域。这样一个数据集就是可分的。

感知机模型

分类函数

​ 重新回到一开始那个图。假设现在我们有一些数据集XXX，有{x10,x20}\{x_{10},x_{20}\}{x10​,x20​}这两个特征值。我们还有个超平面y=w1x1+w2x2y=w_1x_1+w_2x_2y=w1​x1​+w2​x2​。现在我们将这两个特征值输入，会得到下式：
w1x10+w2x20+w0x0=w1x10+w2x20+w0=wTx0+w0w_1x_{10}+w_2x_{20}+w_0x_0=w_1x_{10}+w_2x_{20}+w_0=w^Tx_0+w_0 w1​x10​+w2​x20​+w0​x0​=w1​x10​+w2​x20​+w0​=wTx0​+w0​
​ 根据超平面的性质：如果数据点在超平面之上，则wTx0+w0>0w^Tx_0+w_0>0wTx0​+w0​>0，如果数据点在超平面之下，则wTx0+w0<0w^Tx_0+w_0<0wTx0​+w0​<0。

​ 根据书写习惯，我们将w0w_0w0​换成bbb，单纯换个符号，方便后面区分理解。

​ 但是，对于不同的样本点，其x1,x2x_1,x_2x1​,x2​值不相同，所计算出来的wTx+bw^Tx+bwTx+b肯定也不相同。那我们如何去区分这两个类别呢？

​ 最直观的一种想法就是，让不同的类别对应其特殊的一个常数，比如类别1对应的是0，类别2对应的是1。这就涉及到一个问题，就是要将之前wTx+bw^Tx+bwTx+b的值转化成0和1。而这一步就是fff的作用了。

​ fff称为激活函数，就是将wTx+bw^Tx+bwTx+b转化成0,1。激活函数有很多，我们这使用的是sign函数：
sign(x)={+1,x>0−1,x<0sign(x)=\begin{cases} +1,&x>0\\ -1,&x<0 \end{cases} sign(x)={+1,−1,​x>0x<0​
​ 在上面我们提到超平面的性质，如果点在超平面之上，那么wTx+b>0w^Tx+b>0wTx+b>0，此时正好对应sign函数中的+1，点在超平面之下同理。这也是为什么sign函数能达到分类的目的。于是我们得到感知机的分类函数：
yi=sign(wTx0+b)y_i=sign(w^Tx_0+b) yi​=sign(wTx0​+b)

损失函数

​ 在模型训练的过程中，仅仅有一个分类函数是远远不够的。我们需要有一个损失函数，用来不断优化分类函数中www的权重值。

​ 我们或许可以直接想到，误分类点个数可以作为损失函数的标准：误分类点数目越少，分类越准确。但是这有两个问题：

• 第一个是即使拥有相同的误分类点数目，误分类点距离超平面远近不同，其分类效果也是不一样的。
• 第二个是将误分类点个数作为损失函数难以进行优化。我们知道要减少误分类点的个数，但是具体怎么减少，函数里没有体现。

​ 上面两个问题我们可以通过如下方式进行解决：

​ 首先第一个问题，损失函数需要能够衡量误分类点距离超平面的远近距离。已知点到直线的距离公式为：
d=∣wTx0+b∣∣∣w∣∣d=\frac{|w^Tx_0+b|}{||w||} d=∣∣w∣∣∣wTx0​+b∣​
对于同一条直线，∣∣w∣∣||w||∣∣w∣∣是不会发生变化的，所以可以省去。此外我们可以考虑下误分类点的状况：

• 当超平面上方的点误分类到下方时，所以wTx+b＜0w^Tx+b＜0wTx+b＜0，但是实际上正确的分类yi=+1y_i=+1yi​=+1；
• 当超平面下方的点误分类到上方时，所以wTx+b＞0w^Tx+b＞0wTx+b＞0，但是实际上正确的分类yi=−1y_i=-1yi​=−1；

无论是哪一种情况，都满足yi(wTx+b)<0y_i(w^Tx+b)<0yi​(wTx+b)<0。所以如果我们使用−yi(wTx+b)-y_i(w^Tx+b)−yi​(wTx+b)作为损失函数就可以解决第一个问题，而第二个问题也可以顺便解决。由于要考虑到是多个误分类点，所以我们还要加上∑\sum∑。

这里之所以要填符号是因为我们希望损失函数越小，超平面分类越准确。

所以分类函数为：
L(wi,w0)=−∑xi∈Myi(wTx+b)L(w_i,w_0)=-\sum_{x_i∈M}y_i(w^Tx+b) L(wi​,w0​)=−xi​∈M∑​yi​(wTx+b)

参数更新

​ 有了损失函数之后，我们就可以通过梯度下降进行参数更新，不断优化使分离超平面分类更加准确。

​ 根据梯度下降算法，我们需要对损失函数求偏导：
∇wL(wiT,b)=−∑xi∈Myixi∇bL(wiT,b)=−∑xi∈Myi\nabla_wL(w^T_i,b)=-\sum_{x_i∈M}y_ix_i \\\nabla_bL(w^T_i,b)=-\sum_{x_i∈M}y_i ∇w​L(wiT​,b)=−xi​∈M∑​yi​xi​∇b​L(wiT​,b)=−xi​∈M∑​yi​
然后就可以进行参数更新了：
wT→wT+ηyixib→b+ηyiw^T\to w^T+\eta y_ix_i \\b\to b+\eta y_i wT→wT+ηyi​xi​b→b+ηyi​
其中η\etaη为学习率。

感知机算法的原始形式

所以我们得到了感知机算法：

• 输入：训练集TTT，学习率η\etaη

• 输出：wT，bw^T，bwT，b

感知机模型： f(x)=sign(wT∗x+b)f(x)=sign(w^T∗x+b)f(x)=sign(wT∗x+b)

步骤流程：

(1) 初始化 w0,b0w_0,b_0w0​,b0​。

(2) 在训练集中选取数据 (xi,yi)(x_i,y_i)(xi​,yi​)

(3) 若 yi(wT∗xi+b)≤0y_i(w^T∗x_i+b)≤0yi​(wT∗xi​+b)≤0 (误分类点)，则进行参数更新：

wT→w+ηyixiw^T\to w+ηy_ix_iwT→w+ηyi​xi​

bT→b+ηyib^T\to b+ηy_ibT→b+ηyi​

(4) 转至(2)，直到训练集没有误分类点。

对偶问题

上面我们提到，利用梯度下降进行参数更新：
wT→wT+ηyixib→b+ηyiw^T\to w^T+\eta y_ix_i \\b\to b+\eta y_i wT→wT+ηyi​xi​b→b+ηyi​
如果我们假设样本点(xi,yi)(x_i,y_i)(xi​,yi​)在更新过程中被使用了nin_ini​次，也就是进行了nin_ini​次迭代，所以我们可以得到wT和bw^T和bwT和b的表达式。
wT=∑i=1Nniηyixib=∑i=1Nniηyiw^T=\sum_{i=1}^N n_i\eta y_ix_i \\b=\sum_{i=1}^N n_i\eta y_i wT=i=1∑N​ni​ηyi​xi​b=i=1∑N​ni​ηyi​
将其代入到原始感知机模型当中，
f(x)=sign(wT∗x+b)=sign(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)f(x)=sign(w^T∗x+b)=sign(\sum_{i=1}^N n_i\eta y_ix_i·x+\sum_{i=1}^N n_i\eta y_i) f(x)=sign(wT∗x+b)=sign(i=1∑N​ni​ηyi​xi​⋅x+i=1∑N​ni​ηyi​)
此时学习目标就是nin_ini​

感知机算法的对偶形式

• 输入：训练集TTT，学习率η\etaη

• 输出：nin_ini​

感知机模型： f(x)=sign(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)f(x)=sign(\sum_{i=1}^N n_i\eta y_ix_i·x+\sum_{i=1}^N n_i\eta y_i)f(x)=sign(∑i=1N​ni​ηyi​xi​⋅x+∑i=1N​ni​ηyi​)

步骤流程：

(1) 初始化 $n_i $。

(2) 在训练集中选取数据 (xi,yi)(x_i,y_i)(xi​,yi​)

(3) 若 yi(∑i=1Nniηyixi⋅x+∑i=1Nniηyi)≤0y_i(\sum_{i=1}^N n_i\eta y_ix_i·x+\sum_{i=1}^N n_i\eta y_i)≤0yi​(∑i=1N​ni​ηyi​xi​⋅x+∑i=1N​ni​ηyi​)≤0 (误分类点)，则进行参数更新：

ni→ni+1n_i\to n_i+1ni​→ni​+1

(4) 转至(2)，直到训练集没有误分类点。

也有另外一种写法：

• 输入：训练集TTT，学习率η\etaη

• 输出：αi,b\alpha_i,bαi​,b（αi=niη\alpha_i=n_i\etaαi​=ni​η）

感知机模型： f(x)=sign(∑i=1Nαiyixi⋅x+b)f(x)=sign(\sum_{i=1}^N\alpha_i y_ix_i·x+b)f(x)=sign(∑i=1N​αi​yi​xi​⋅x+b)

步骤流程：

(1) 初始化 nin_ini​。

(2) 在训练集中选取数据 (xi,yi)(x_i,y_i)(xi​,yi​)

(3) 若 yi(∑i=1Nniηyixi⋅x+b)≤0y_i(\sum_{i=1}^N n_i\eta y_ix_i·x+b)≤0yi​(∑i=1N​ni​ηyi​xi​⋅x+b)≤0 (误分类点)，则进行参数更新：

αi→αi+η\alpha_i\to \alpha_i+\etaαi​→αi​+η

b→b+ηyib\to b+\eta y_ib→b+ηyi​

(4) 转至(2)，直到训练集没有误分类点。