计算机断层重建(CT)是一个比较热门的领域，这篇文章简单介绍了反投影方法的重建过程。

参考资料：冈萨雷斯，《数字图像处理》，电子工业出版社。

文章目录

• 直接反投影
• 投影与Radon变换
• 滤波反投影法(FBP)
• • 傅里叶切片定理
  • 平行射线下的滤波反投影重建
  • 卷积与傅里叶反变换

直接反投影

该方法是沿着射线来的方向把一维信号反投影回去，可以想象成把投影穿过图像区域反“涂抹”回去。注意到相隔180°的投影互为镜像，因此，为了产生重建所要求的所有投影，只需要按照圆周的一半角度增量来考虑即可。下图是不同投影角度数量下直接反投影法的结果

从图中可以看到，直接反投影法有明显的伪影，也被称之为“晕环”。伪影的亮度比物体第，但比背景高。越多的投影使得伪影亮度越低，但会带来模糊。在CT重建中，去除伪影是一个重要的问题。

投影与Radon变换

Radon变换描述了投影产生时的数学过程。考虑直线y=ax+by=ax+by=ax+b，将其用极坐标来表示可写为：
xcos⁡θ+ysin⁡θ=ρx\cos\theta+y\sin\theta=\rhoxcosθ+ysinθ=ρ
对于图像f(x,y)f(x,y)f(x,y)，沿该线积分为：
g(ρ,θ)=∫−∞∞∫−∞∞f(x,y)δ(xcos⁡θ+ysin⁡θ−ρ)dxdyg(\rho,\theta)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(x\cos\theta+y\sin\theta-\rho)dxdyg(ρ,θ)=∫−∞∞​∫−∞∞​f(x,y)δ(xcosθ+ysinθ−ρ)dxdy
其中δ\deltaδ为示性函数，或者是和示性函数差不多的冲激函数。离散情况下可写为：
g(ρ,θ)=∑0M−1∑0N−1f(x,y)δ(xcos⁡θ+ysin⁡θ−ρ)g(\rho,\theta)=\sum_{0}^{M-1}\sum_{0}^{N-1}f(x,y)\delta(x\cos\theta+y\sin\theta-\rho)g(ρ,θ)=0∑M−1​0∑N−1​f(x,y)δ(xcosθ+ysinθ−ρ)

进一步可以得到直接反投影的数学表示：
f(x,y)=∫0πg(ρ,θ)dθf(x,y)=\int_0^{\pi}g(\rho,\theta)d\thetaf(x,y)=∫0π​g(ρ,θ)dθ

滤波反投影法(FBP)

傅里叶切片定理

关于ρ\rhoρ投影的一维傅里叶变换为
G(ω,θ)=∫−∞∞g(ρ,θ)e−j2πωρdρG(\omega,\theta)=\int_{-\infty}^{\infty}g(\rho,\theta)e^{-j2\pi\omega\rho}d\rhoG(ω,θ)=∫−∞∞​g(ρ,θ)e−j2πωρdρ
傅里叶变换可以看成从空间域到频率域上的转换，这里ω\omegaω为频率变量。将ggg带入上式中可得：
G(ω,θ)=∫−∞∞∫−∞∞∫−∞∞f(x,y)δ(xcos⁡θ+ysin⁡θ−ρ)e−j2πωρdxdydρ=∫−∞∞∫−∞∞f(x,y)[∫−∞∞δ(xcos⁡θ+ysin⁡θ−ρ)e−j2πωρdρ]dxdy=∫−∞∞∫−∞∞f(x,y)e−j2πω(xcos⁡θ+ysin⁡θ)dxdy=F(ωcos⁡θ,ωsin⁡θ)\begin{aligned} G(\omega,\theta)&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(x\cos\theta+y\sin\theta-\rho)e^{-j2\pi\omega\rho}dxdyd\rho \\ &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\left[\int_{-\infty}^{\infty}\delta(x\cos\theta+y\sin\theta-\rho)e^{-j2\pi\omega\rho}d\rho\right]dxdy \\ &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-j2\pi\omega(x\cos\theta+y\sin\theta)}dxdy \\ &=F(\omega\cos\theta,\omega\sin\theta) \end{aligned} G(ω,θ)​=∫−∞∞​∫−∞∞​∫−∞∞​f(x,y)δ(xcosθ+ysinθ−ρ)e−j2πωρdxdydρ=∫−∞∞​∫−∞∞​f(x,y)[∫−∞∞​δ(xcosθ+ysinθ−ρ)e−j2πωρdρ]dxdy=∫−∞∞​∫−∞∞​f(x,y)e−j2πω(xcosθ+ysinθ)dxdy=F(ωcosθ,ωsinθ)​
其中F(u,v)F(u,v)F(u,v)为f(x,y)f(x,y)f(x,y)的二维傅里叶变换，即：
F(u,v)=∫−∞∞∫−∞∞f(x,y)e−j2π(ux+vy)dxdyF(u,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-j2\pi(ux+vy)}dxdyF(u,v)=∫−∞∞​∫−∞∞​f(x,y)e−j2π(ux+vy)dxdy

这说明了，对投影ggg的一维傅里叶变换，等于对图像fff二维傅里叶变换在某一条线下的切片。这就是傅里叶切片定理。

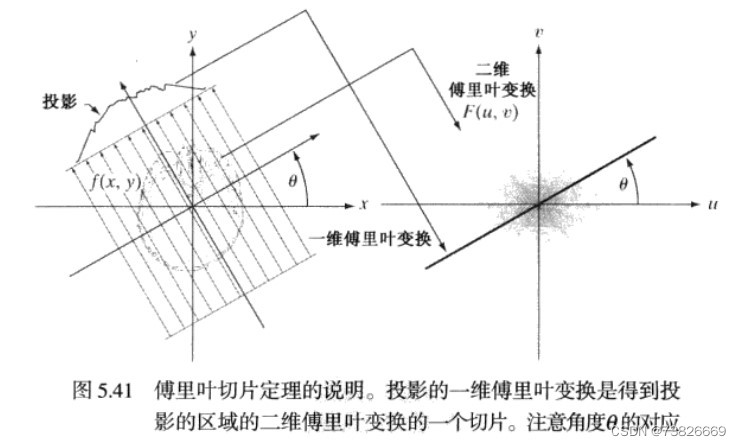
平行射线下的滤波反投影重建

傅里叶逆变换：
f(x,y)=∫−∞∞∫−∞∞F(u,v)ej2π(ux+vy)dudvf(x,y)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(u,v)e^{j2\pi(ux+vy)}dudvf(x,y)=∫−∞∞​∫−∞∞​F(u,v)ej2π(ux+vy)dudv
令u=ωcos⁡θ,v=ωsin⁡θu=\omega\cos\theta,v=\omega\sin\thetau=ωcosθ,v=ωsinθ，则有
f(x,y)=∫02π∫−∞∞F(ωcos⁡θ,ωsin⁡θ)ej2πω(xcos⁡θ+ysin⁡θ)ωdωdθf(x,y)=\int_{0}^{2\pi}\int_{-\infty}^{\infty}F(\omega\cos\theta,\omega\sin\theta)e^{j2\pi\omega(x\cos\theta+y\sin\theta)}\omega d\omega d\thetaf(x,y)=∫02π​∫−∞∞​F(ωcosθ,ωsinθ)ej2πω(xcosθ+ysinθ)ωdωdθ
应用傅里叶切片定理，以及G(ω,θ+π)=G(−ω,θ)G(\omega,\theta+\pi)=G(-\omega,\theta)G(ω,θ+π)=G(−ω,θ)可得
f(x,y)=∫02π∫−∞∞G(ω,θ)ej2πω(xcos⁡θ+ysin⁡θ)ωdωdθ=∫0π[∫−∞∞∣w∣G(ω,θ)ej2πωρdω]ρ=xcos⁡θ+ysin⁡θdθ\begin{aligned} f(x,y)&=\int_{0}^{2\pi}\int_{-\infty}^{\infty}G(\omega,\theta)e^{j2\pi\omega(x\cos\theta+y\sin\theta)}\omega d\omega d\theta \\ &=\int_{0}^{\pi}\left[\int_{-\infty}^{\infty}|w|G(\omega,\theta)e^{j2\pi\omega\rho}d\omega\right]_{\rho=x\cos\theta+y\sin\theta}d\theta \end{aligned} f(x,y)​=∫02π​∫−∞∞​G(ω,θ)ej2πω(xcosθ+ysinθ)ωdωdθ=∫0π​[∫−∞∞​∣w∣G(ω,θ)ej2πωρdω]ρ=xcosθ+ysinθ​dθ​

方括号里可以看成一维傅里叶逆变换，只是附加了∣ω∣|\omega|∣ω∣项，这一项可以看为一个斜坡滤波器。因为∣ω∣|\omega|∣ω∣在无穷处都到达+∞+\infty+∞,所以傅里叶反变换无定义。实践中常常通过加窗的方式，使它在定义的范围之外为0。

简单的方法是通过方波限制，但方波有不希望的振铃特性，这会为图像重建带来伪影。因此可以考虑平滑窗，比如汉明窗或者韩窗：
h(w)={c+(c−1)cos⁡2πωM−10⩽ω⩽(M−1)0其他h(w)=\left\{ \begin{aligned} &c+(c-1)\cos\frac{2\pi\omega}{M-1} \qquad &0\leqslant\omega\leqslant(M-1) \\ &0 \qquad &其他 \end{aligned}\right. h(w)=⎩⎨⎧​​c+(c−1)cosM−12πω​0​0⩽ω⩽(M−1)其他​

总结： 获得完整反投影图像是由如下步骤得到的：

• 计算每个投影的一维傅里叶变换。
• 用滤波函数∣ω∣|\omega|∣ω∣乘以每个傅里叶变换，即乘以一个合适的窗。
• 得到每个滤波后的变换的一维傅里叶反变换。
• 对所有的一维反变换积分（求和）。

卷积与傅里叶反变换

考虑傅里叶反变换可以写成卷积的形式，可以有
f(x,y)=∫0π[∣ω∣G(ω,θ)ej2πωρdω]ρ=xcos⁡θ+ysin⁡θdθ=∫0π[s(ρ)⋆g(ρ,θ)]ρ=xcos⁡θ+ysin⁡θdθ=∫0π[∫−∞∞g(ρ,θ)s(xcos⁡θ+ysin⁡θ−ρ)dρ]dθ\begin{aligned} f(x,y)&=\int_0^{\pi}\left[|\omega|G(\omega,\theta)e^{j2\pi\omega\rho}d\omega\right]_{\rho=x\cos\theta+y\sin\theta}d\theta \\ &=\int_0^{\pi}\left[s(\rho)\star g(\rho,\theta)\right]_{\rho=x\cos\theta+y\sin\theta}d\theta \\ &=\int_0^{\pi}\left[\int_{-\infty}^{\infty}g(\rho,\theta)s(x\cos\theta+y\sin\theta-\rho)d\rho\right]d\theta \end{aligned} f(x,y)​=∫0π​[∣ω∣G(ω,θ)ej2πωρdω]ρ=xcosθ+ysinθ​dθ=∫0π​[s(ρ)⋆g(ρ,θ)]ρ=xcosθ+ysinθ​dθ=∫0π​[∫−∞∞​g(ρ,θ)s(xcosθ+ysinθ−ρ)dρ]dθ​
其中⋆\star⋆表示卷积，s(ρ)s(\rho)s(ρ)表示∣ω∣|\omega|∣ω∣的傅里叶逆变换。

注：

• 重建过程中不需要存储所有的反投影图像，单个求和运算仅被最后的反投影图像更新。
• 斜坡滤波器在频率域的直流项归零，故每幅反投影图像的均值将为零。这意味着每幅反投影图像都将有负像素和正像素。简单的解决办法是所有像素减去最小值再放缩。
  f′=K[f−min⁡fmax⁡(f−minf)]f'=K\left[\frac{f-\min{f}}{\max{(f-min{f})}}\right]f′=K[max(f−minf)f−minf​]