编译原理陈火旺版第三章课后题答案
下面答案仅供参考!
1.编写一个对于 Pascal 源程序的预处理程序。该程序的作用是,每次被调用时都将 下一个完整的语句送进扫描缓冲区,去掉注解行,同时要对源程序列表打印。
答:以下是一个简单的预处理程序的实现,其功能为将注释行删除并将每个完整语句放入扫描缓冲区中,同时打印原始源代码和处理后的代码:
program Preprocessor;
usesSysUtils;
varInputFile, OutputFile: TextFile;Line: string;InComment: Boolean;
begin// 打开输入和输出文件AssignFile(InputFile, 'input.pas');AssignFile(OutputFile, 'output.pas');Reset(InputFile);Rewrite(OutputFile);// 初始化变量Line := '';InComment := False;try// 逐行读取输入文件while not Eof(InputFile) dobeginReadLn(InputFile, Line);// 如果当前行是注释行,则跳过if Pos('//', Line) = 1 thenContinue;// 如果当前行包含 "(*",则标记为在注释中if Pos('(*', Line) > 0 thenInComment := True;// 如果当前行不在注释中,则将其添加到缓冲区中if not InComment thenWriteLn(OutputFile, Line);// 如果当前行包含 "*)",则标记为不在注释中if Pos('*)', Line) > 0 thenInComment := False;end;// 关闭文件CloseFile(InputFile);CloseFile(OutputFile);// 打印源代码和处理后的代码Reset(InputFile);Reset(OutputFile);WriteLn('Original source code:');while not Eof(InputFile) dobeginReadLn(InputFile, Line);WriteLn(Line);end;WriteLn;WriteLn('Processed source code:');while not Eof(OutputFile) dobeginReadLn(OutputFile, Line);WriteLn(Line);end;excepton E: Exception doWriteln(E.ClassName, ': ', E.Message);end;
end.在上面的代码中,我们使用 InComment 变量来跟踪当前是否在注释行中。如果当前行包含 "(",则将 InComment 设置为 True,如果包含 ")",则将其设置为 False。在读取每个非注释行时,我们将其添加到输出文件中,并在处理后打印原始源代码和处理后的代码。
3.用类似C或Pascal的语言编写过程GetChar, GetBC 和 Concat
varsource: string; // 输入的字符串index: integer; // 当前字符在字符串中的位置
// 从输入的字符串中获取下一个字符
function GetChar(): char;
beginif index <= length(source) thenbeginGetChar := source[index];index := index + 1;endelseGetChar := #0; // 如果已经到达字符串末尾,则返回空字符
end;
// 跳过输入字符串中的空白字符
procedure GetBC();
beginwhile (index <= length(source)) and (source[index] in [' ', #9, #13, #10]) doindex := index + 1;
end;
// 将两个字符串拼接在一起
function Concat(s1: string; s2: string): string;
vari: integer;
beginConcat := ''; // 初始化返回的字符串for i := 1 to length(s1) doConcat := Concat + s1[i];for i := 1 to length(s2) doConcat := Concat + s2[i];
end;在上面的代码中,我们使用一个字符串变量 source 存储输入的字符串,并使用一个整数变量 index 来跟踪当前字符在字符串中的位置。GetChar 过程返回下一个字符,并将 index 增加 1。GetBC 过程用于跳过字符串中的空白字符,包括空格、制表符、回车符和换行符。Concat 过程接受两个字符串参数 s1 和 s2,并将它们拼接在一起返回一个新的字符串。在 Concat 过程中,我们使用一个循环将 s1 中的字符逐一添加到返回字符串中,然后再将 s2 中的字符逐一添加到返回字符串中。
6.令 A、B 和 C 是任意正规式,证明以下关系成立:

答案:

(3)





7.构造下列正规式相应的 DFA
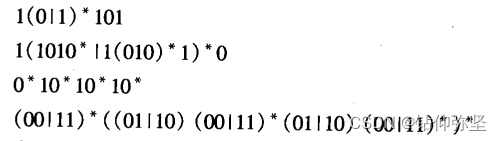
第一个:1(0|1)*101
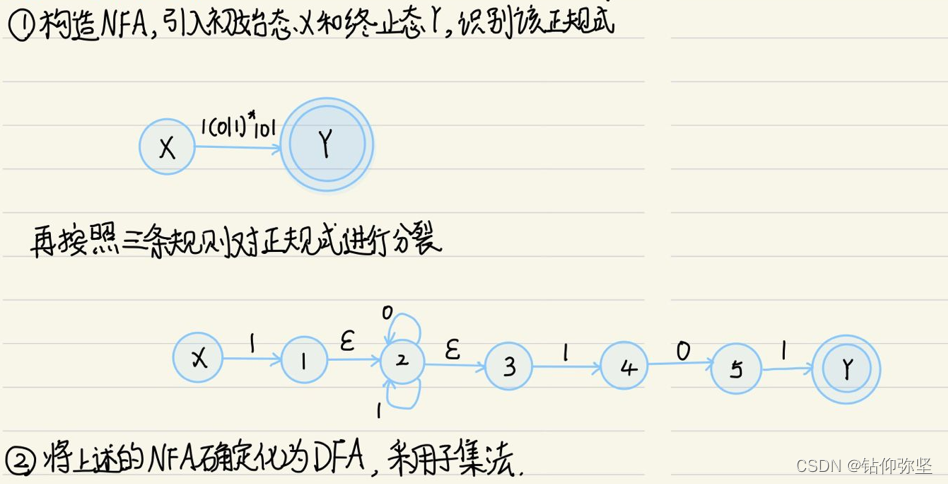


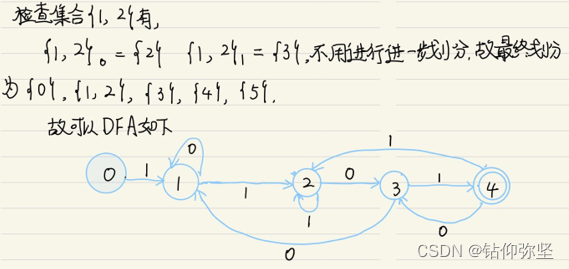
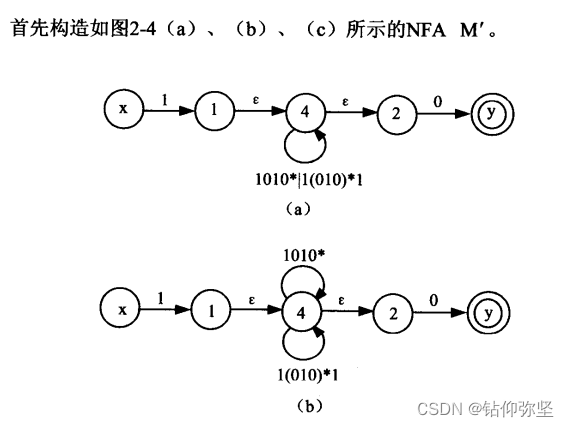
第二个: 1(1010*l1(010)*1)*0
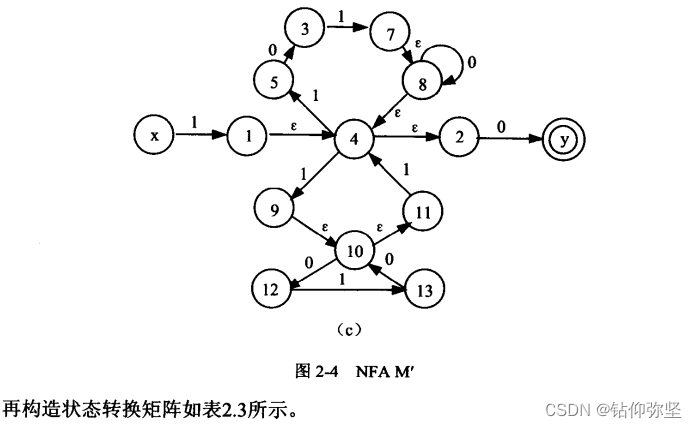
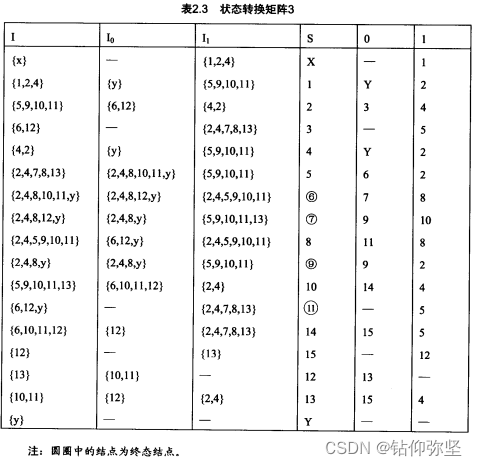

第三个:
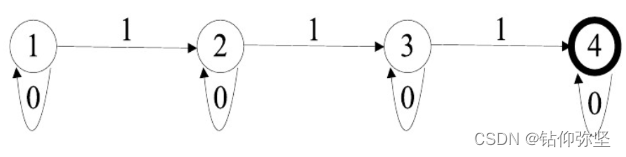
第四个:
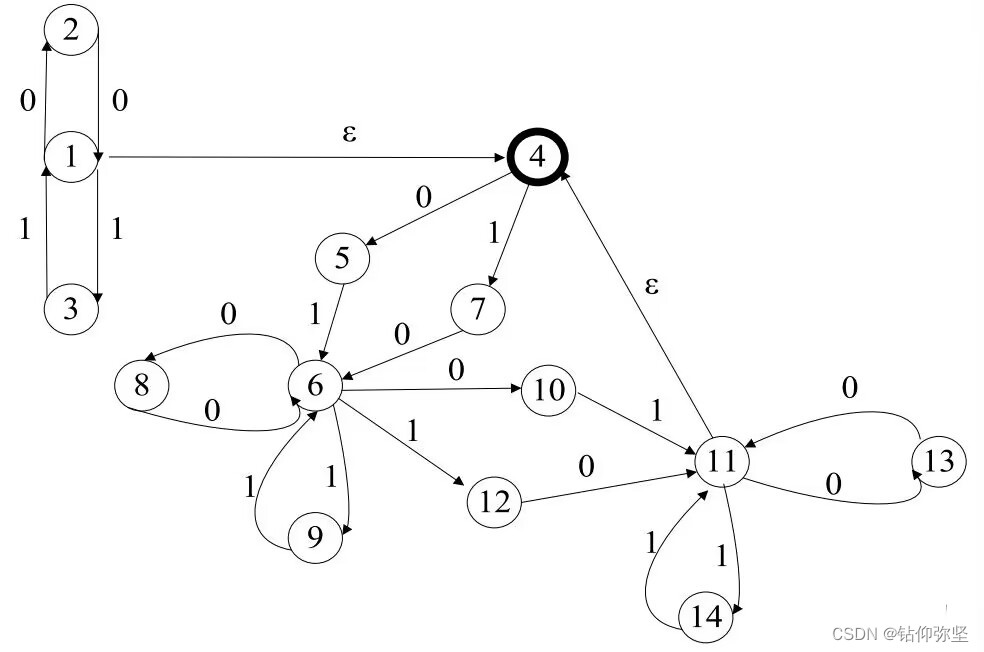
8. 给出下面正规表达式:
(1)以 01 结尾的二进制数串;
(1)分析题意,要求的是二进制串,即由0和1构成的串,并且必须以 01 结尾,所以本题可以分两部分去完成,一部分实现由0和1构成的任意串,一部分即 01,然后将它们 连接到一起就可以了,所以本题的解答是:(1|0)*01。
(2)能被 5 整除的十进制整数;
分析题意,本题要求是十进制整数,也就是由 0...9 这 10 个数字组成的字符串, 并且不能以 0 开头(整数“0”除外),要求能被 5 整除,则该串必须以 0 或者 5 结尾。根据我们的分析,可以把本题分成两种情况考虑:一种情况是该整数只有 1 位,则该整数有 0 和5 两种可能;另外一种情况是该整数有多位,则该整数可以分成 3 部分考虑,一是第 1 位必须不为 0,二是最后 1 位必须为 0或 5,三是中间部分可有可无,并且可以由 0 ~ 9 之间任意数字构成,所以本题的正规表达式为:
(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*(0|5)(0|5)
(3) 包含奇数个1或奇数个0的二进制数串;
本题求二进制串,并且要求包含奇数个 0或奇数个 1,由于 0 和 1 都可以在二进 制串中任何地方出现,所以本题只需要考虑一种情况,另外一种情况也可以类似求得。考虑包含奇数个0的字符串:由于只关心0的个数的奇偶数,我们可以把二进制串分成多段来考虑,第 1 段为二进制串的开始到第 1 个 0 为止,这一段包含 1 个 0,并且0的前面有 0 个或多个 1,对于剩下的二进制串按照每段包含两个 0 的方式去划分,即以 0 开始,以 0 结尾,中间可以有 0 个或多个 1,如果一个二进制串被这样划分完后,剩下的部分如果全 部是全 1 串(这些全 1 串在前面划分的串之间或最后),则该二进制串就具有奇数个 0,所 以该二进制串可以这样描述:以第 1 段(ro)开始,后面由全 1 串(r )以及包含两个0的 串(or o)组成,所以包含奇数个 o 的正规表达式为:广o(11or o) # ,本题的解答则是:广 0(1101 * 0) * 1 0 * 1(0110* 1) *。
(4)英文字母组成的所有符号串,要求符号串中的字母依照字典序排列;
(5)没有重复出现的数字的数字符号串的全体;

(6) 最多有一个重复出现的数字的数字符号串的全体;
其中
(7) 不包含子串 abb 的由 a 和 b 组成的符号串的全体。
10.一个人带着狼、山羊和白菜在一条河的左岸,有一条船,大小正好能装下 这个人和其它 3 件东西中的一件。人和他的随行物都要过到河的右岸。人每次只能将一 件东西摆渡过河。但若人将狼和羊留在同一岸而无人照顾的话,狼将把羊吃掉,类似的, 羊也可能会吃掉白菜。请问是否有可能摆渡过河,并使得羊和白菜都不会被吃掉?如果 可能,请用有限自动机写出渡河的方法。
答:这是一道经典的智力题,很显然是有办法渡河的,关键是如何用有限自动机来求解渡河的方法。有限自动机描述的是状态和状态之间的转换,对于本题,可以把人、狼、山羊和白菜都在左岸作为有限自动机的初始状态,而把他们都在右岸作为终止状态,只要构造一 个自动机使得存在一条从初始状态到终止状态的路径就可以了。


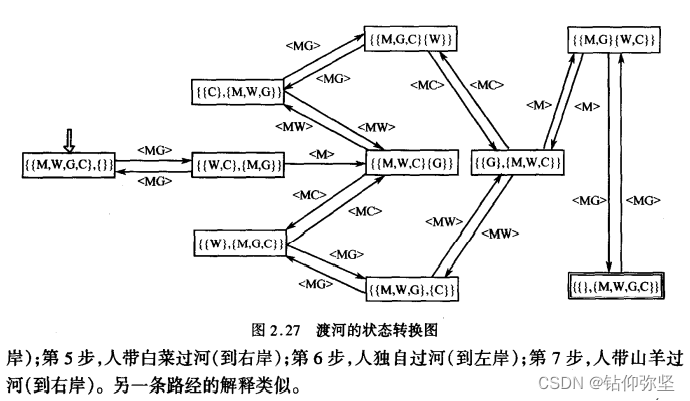
11.用某种高级语言写出:
(1)将正规式变成 NFA 的算法;

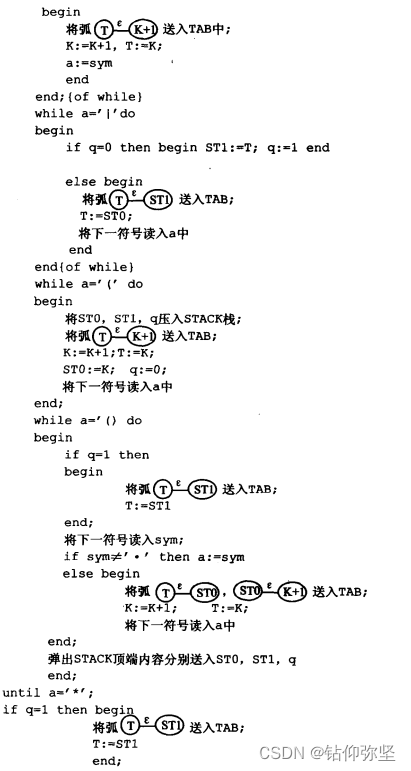
(2) 将 NFA 确定化的算法;


(3) DFA 状态最少化的算法。
假定DFA有N个状态,我们用{}i表示已分解了的状态子集,用{}i'表示临时分解的状态子集;而M是根据定义不断扩大的非等价的状态子集个数;P是在M扩大前的非等价的状态子集个数。只有当M不再扩大时,有P=M,则其算法可描述如下:


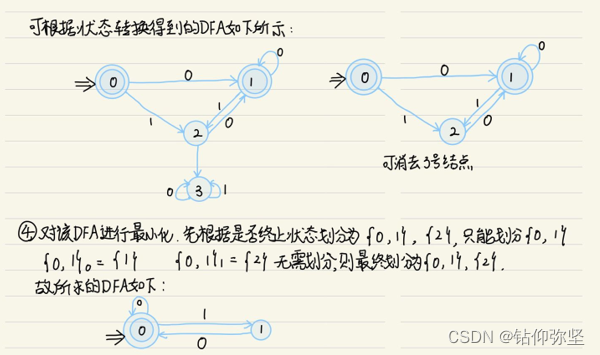
12.将图 3.18的(a)和(b)分别确定化和最少化。
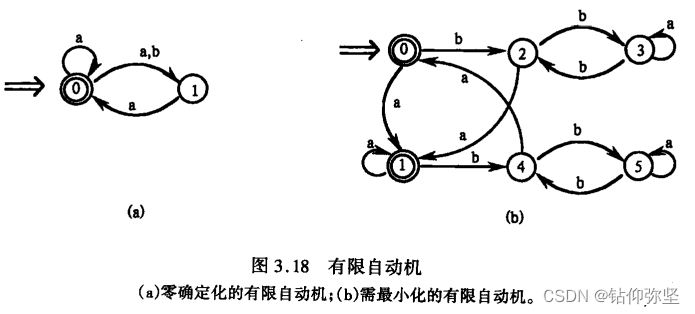
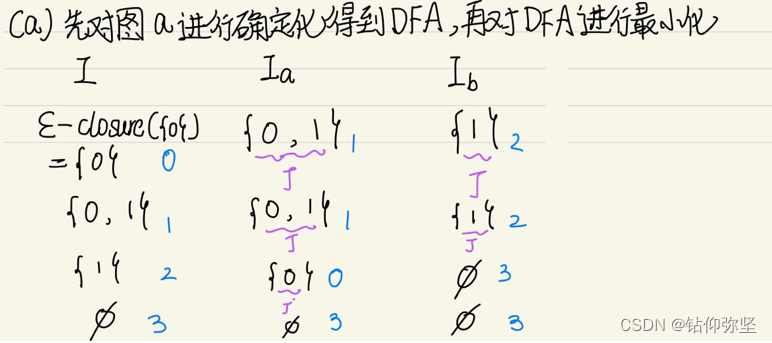
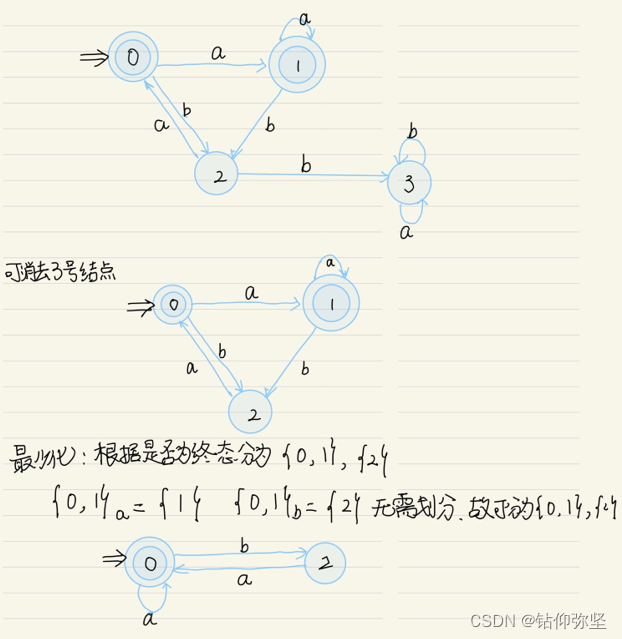
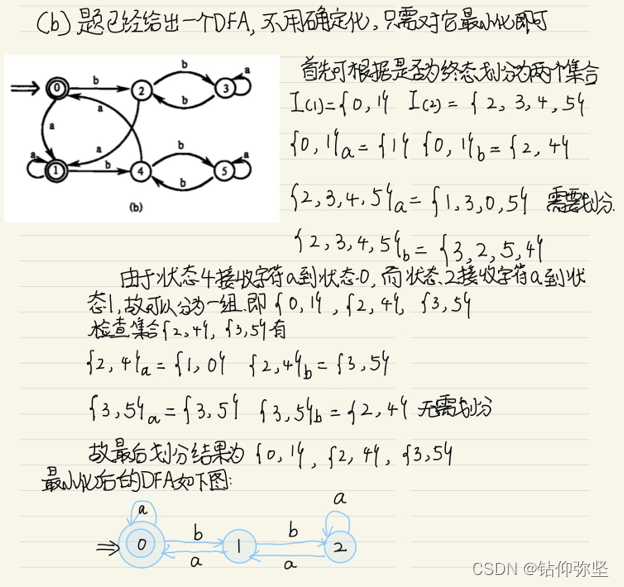
14.构造一个 DFA,它接受![]() = { 0,1 }上所有满足如下条件的字符串:每个1都有0直接跟在右边。
= { 0,1 }上所有满足如下条件的字符串:每个1都有0直接跟在右边。

15.给定右线性文法 G:

求出一个与 G 等价的左线性文法。
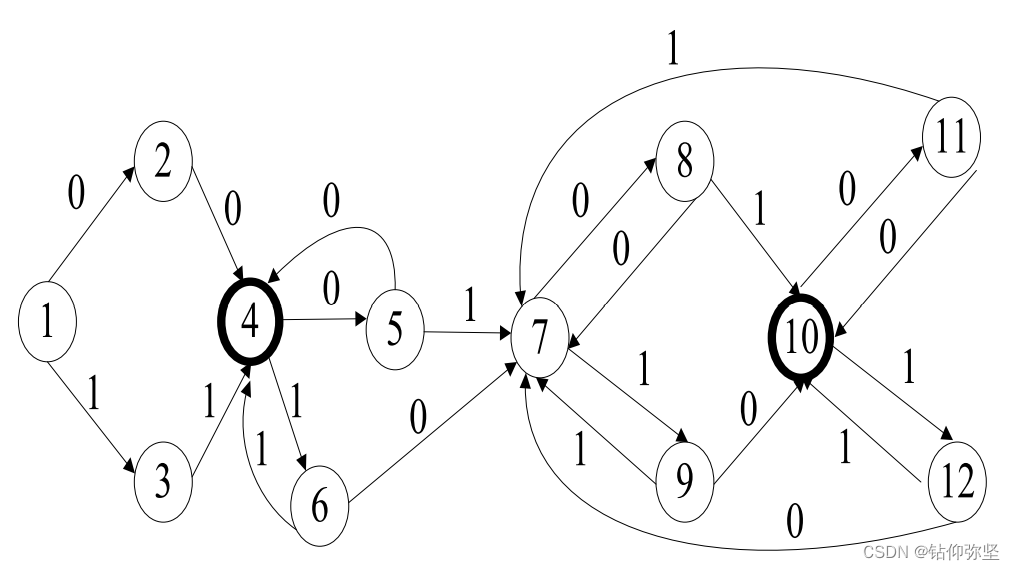
解题思路:根据右线性文法求左线性文法没有直接的方法,但可以通过状态转换图去转换。可 以先求出文法 G 的状态转换图,再根据状态转换图写出相应的左线性文法。文法 G 所对应的状态转换图如下图所示。
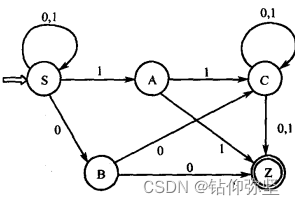
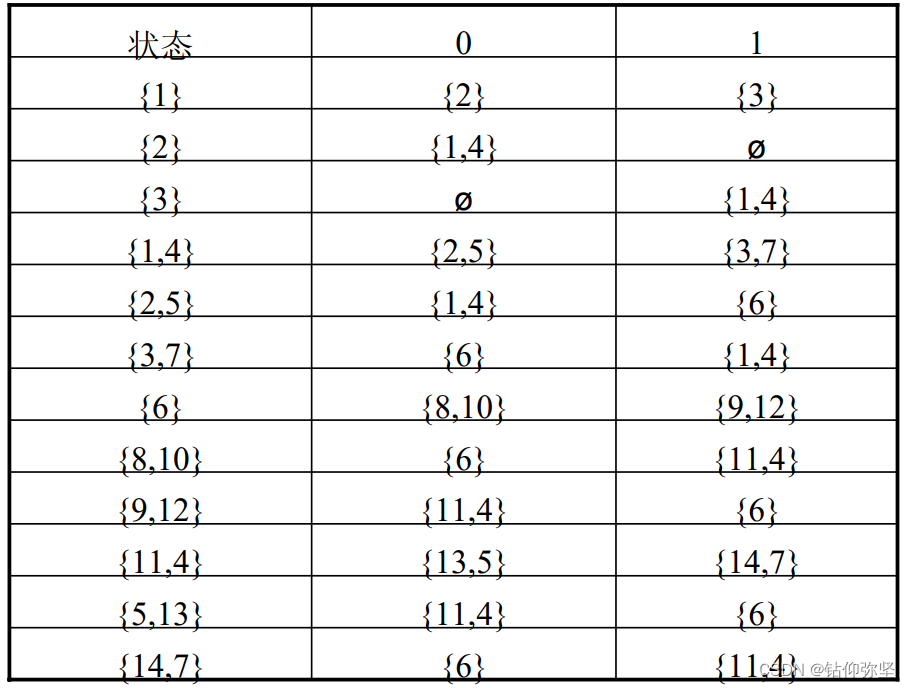
对上图中的状态转换图进行确定化,得到表 2.12。 给状态编号,得到表 2,13 所列的状态转换矩阵。
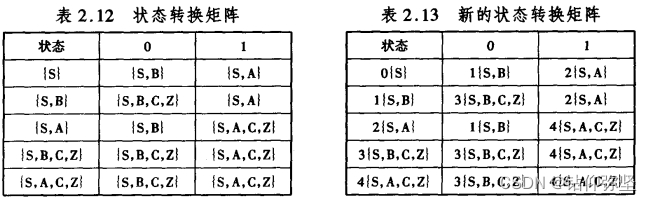
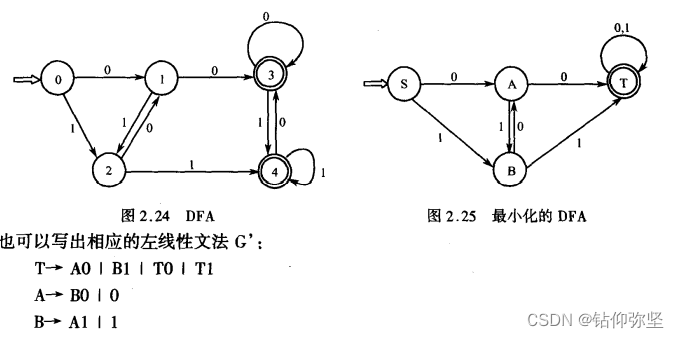
根据状态转换矩阵获得如图 2.24 所示的 DFA。 还可以对上图的 DFA 进行化简,状态 3 和 4 可以合并,化简后的 DFA 如图 2.25 所示。
不难看出,该 DFA 接受的语言是{0,1}上包含00 或11的字符串。根据图2.25,我们
20.假定有如下辅助定义式:
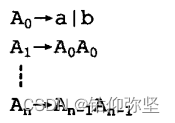
(1)把中所有简名都换掉,最终所得的正规式的长度是多少?
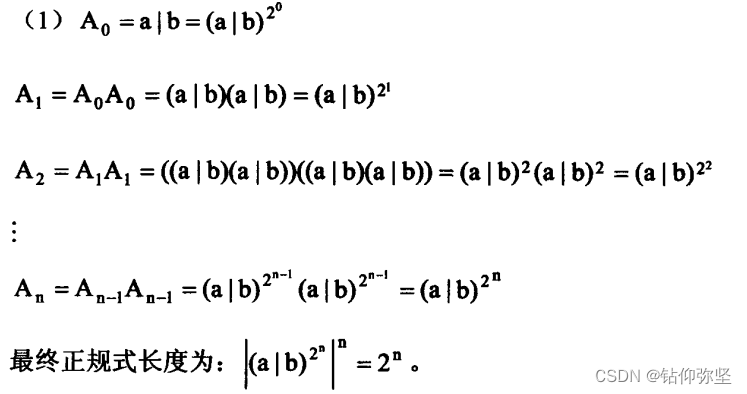
(2)字集的元素是什么?把它们非形式地表示成n的函数;
![]()
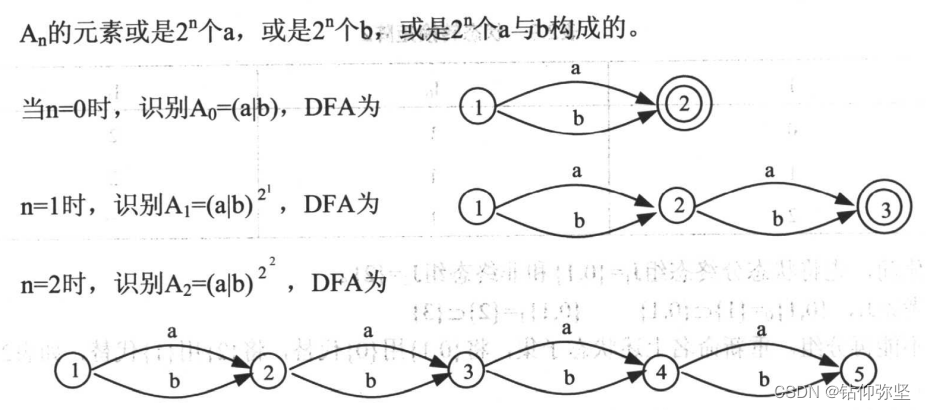
(3)证明识别的DFA只需用
个状态就足够了。

