PCA的定义

• 主成分分析，即Principal Component Analysis（PCA），是多元统计中的重要内容，也广泛应用于机器学习和其它领域。它的主要作用是对高维数据进行降维。PCA把原先的n个特征用数目更少的k个特征取代，新特征是旧特征的线性组合，这些线性组合最大化样本方差，尽量使新的k个特征互不相关。

PCA的实现步骤

1. 计算样本每个特征的平均值；

2. 每个样本数据减去该特征的平均值；

3. 对样本组成的矩阵求协方差矩阵；

4. 对协方差矩阵做分解得到特征值和特征向量，并将特征值和特征向量重新按照降序排列；

5. 对特征值求取累计贡献率；

6. 通过累计贡献率选取适合的特征向量子集合；

7. 对原始数据进行转换

注意：假设有m个样本，每个样本有n个特征，即组成m行n列的矩阵A,如果是图像的话，由于图像是二维向量，所以先要将图像转换为一个行向量。求均值是对A矩阵的每一列求均值，此处协方差矩阵应该是A.T * A而不是A*A.T,最后得到的协方差矩阵的形状应为n*n。

协方差矩阵分解

1. 原始算法（硬算，特征数很大时计算量非常大）

2. numpy的svd算法来分解（使用svd分解出来的右奇异矩阵和直接求出来的特征向量矩阵是一个意思，但是svd并不是通过协方差矩阵来计算的，而是通过某种强大的算法近似求解）

3. scikit-learn实现的PCA

PCA实现

mat = [[-1,-1,0,2,1],[2,0,0,-1,-1],[2,0,1,1,0]]
mat = np.array(mat)
#原始算法
def origin_algorithm_pca(mat, 2):#对列求均值mean = np.mean(mat, 0)#去中心化A = mat - mean#求方差矩阵cov = np.dot(A.T, A)/2#求解协方差矩阵的特征值和特征向量s, vector = np.linalg.eig(cov)#对特征进行压缩compression = np.dot(A, vector[:2,:].T)return compressiondef numpy_svd(mat, 2):#对列求均值mean = np.mean(mat, 0)#去中心化A = mat - mean#u,s,VT = np.linalg.svd(A)#压缩compression = np.dot(A, VT[:2,:])return compression

PCA实现人脸识别

1. 将每张图像拉直为一维行向量

2. 将所有样本存储为矩阵形式，矩阵的每一列表示图像的一个特征也是一个像素

3. 按列求取均值，并用原始矩阵减去均值

4. 利用A.T * A得到协方差矩阵(这一步代码中直接利用svd方法得到U,S,VT)

5. 将原始矩阵乘以VT得到压缩后的矩阵，将VT存储起来用于测试测试样本

6. train_A*VT和test_A*VT，将test_A*VT中的每个样本与train_A*VT计算平方差，并按行求和后排序，得到距离最小的对应的train_A的label，就是预测结果

7. 根据预测结果和真实标签计算准确率

# coding:utf-8
import os
from numpy import *
import numpy as np
import cv2
import matplotlib.pyplot as plt
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei']# 图片矢量化
def img2vector(image):img = cv2.imread(image, 0)  # 读取图片rows, cols = img.shape  #获取图片的像素imgVector = np.zeros((1, rows * cols))imgVector = np.reshape(img, (1, rows * cols))#使用imgVector变量作为一个向量存储图片矢量化信息，初始值均设置为0return imgVectororlpath = "./ORL"# 读入人脸库,每个人随机选择k张作为训练集,其余构成测试集
def load_orl(k):#参数K代表选择K张图片作为训练图片使用'''对训练数据集进行数组初始化，用0填充，每张图片尺寸都定为112*92,现在共有40个人，每个人都选择k张，则整个训练集大小为40*k,112*92'''train_face = np.zeros((40 * k, 112 * 92))train_label = np.zeros(40 * k)  # [0,0,.....0](共40*k个0)test_face = np.zeros((40 * (10 - k), 112 * 92))test_label = np.zeros(40 * (10 - k))# sample=random.sample(range(10),k)#每个人都有的10张照片中，随机选取k张作为训练样本(10个里面随机选取K个成为一个列表)sample = random.permutation(10) + 1  # 随机排序1-10 (0-9）+1for i in range(40):  # 共有40个人people_num = i + 1for j in range(10):  # 每个人都有10张照片image = orlpath + '/s' + str(people_num) + '/' + str(sample[j]) + '.jpg'# 读取图片并进行矢量化img = img2vector(image)if j < k:# 构成训练集train_face[i * k + j, :] = imgtrain_label[i * k + j] = people_numelse:# 构成测试集test_face[i * (10 - k) + (j - k), :] = imgtest_label[i * (10 - k) + (j - k)] = people_numreturn train_face, train_label, test_face, test_label# 定义PCA算法
def PCA(data, r):#降低到r维data = np.float32(np.mat(data))rows, cols = np.shape(data)# print(rows, cols)data_mean = np.mean(data, 0)  # 对列求平均值A = data - np.tile(data_mean, (rows, 1))  # 将所有样例减去对应均值得到Au, s, VT = np.linalg.svd(A) #利用svd求解右奇异向量即需要将原始数组映射的向量空间矩阵V_r = VT[:, 0:r]  # 按列取前r个特征向量#将原始数据乘上新的空间向量得到降维后的矩阵final_data = A * V_rreturn final_data, data_mean, V_rdef face_recongize():for r in range(10, 81, 10):  # 最多降到40维,即选取前40个主成分（因为当k=1时，只有40维)print("当降维到%d时" % (r))x_value = []y_value = []train_face, train_label, test_face, test_label = load_orl(7)  # 得到数据集# 利用PCA算法进行训练data_train_new, data_mean, V_r = PCA(train_face, r)# print(data_train_new.shape)num_train = data_train_new.shape[0]  # 训练脸总数num_test = test_face.shape[0]  # 测试脸总数temp_face = test_face - np.tile(data_mean, (num_test, 1))data_test_new = temp_face * V_r  # 得到测试脸在特征向量下的数据data_test_new = np.array(data_test_new)  # mat change to array# print(data_test_new.shape)data_train_new = np.array(data_train_new)# 测试准确度true_num = 0for i in range(num_test):testFace = data_test_new[i, :]# print(testFace.shape)diffMat = data_train_new - np.tile(testFace, (num_train, 1))  # 训练数据与测试脸之间距离print(diffMat.shape)sqDiffMat = diffMat ** 2sqDistances = sqDiffMat.sum(axis=1)  # 按行求和sortedDistIndicies = sqDistances.argsort()  # 对向量从小到大排序，使用的是索引值,得到一个向量indexMin = sortedDistIndicies[0]  # 距离最近的索引if train_label[indexMin] == test_label[i]:true_num += 1else:passaccuracy = float(true_num) / num_testx_value.append(7)y_value.append(round(accuracy, 2))print('当每个人选择%d张照片进行训练时，The classify accuracy is: %.2f%%' % (7, accuracy * 100))if __name__ == '__main__':face_recongize()

PCA的优缺点

1. 优点

• 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。

• 各主成分之间正交，可消除原始数据成分间的相互影响的因素

• 计算方法简单，主要运算是特征值分解，易于实现。

2. 缺点

• 主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

• 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

SVD原理

任意形状的矩阵A经过svd分解会得到U，Σ，VT（V的转置）三个矩阵，其中U是一个M×M的方阵，被称为左奇异向量，方阵里面的向量是正交的；Σ是一个M×N的对角矩阵，除了对角线的元素其他都是0，对角线上的值称为奇异值；VT(V的转置)是一个N×N的矩阵，被称为右奇异向量，方阵里面的向量也都是正交的。

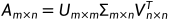
可以计算ΣΣ前x个奇异值的平方和占所有奇异值的平方和的比例，如果大于90%，我们就选这x个奇异值重构矩阵（剩余的数据代表的可能是噪声，无用数据）。

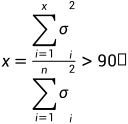
那么重构的A'为：

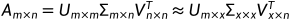
SVD的应用

• svd实现图像压缩

import scipy.misc
from scipy.linalg import svd
import matplotlib.pyplot as plt
import numpy as np
import numpy
img = scipy.misc.face()[:,:,0]
img = np.array(img)
U,s,Vh=svd(img)
#将特征压缩到十维，并还原图像
A = numpy.dot(U[:,0:10],numpy.dot(numpy.diag(s[0:10]),Vh[0:10,:]))
plt.subplot(111,aspect='equal')
plt.title(":10")
plt.imshow(A)
plt.imsave('a10.png', A)

• svd实现信号去噪

import matplotlib.pylab as plt
import numpy as np
import numpy
from scipy.linalg import svd
x = np.linspace(-np.pi, np.pi, 400)
mu, sigma = 0, 0.05
ss = np.random.normal(mu, sigma, 400)
a = (np.sin(x) + ss).reshape(20, 20)U,s,Vh = svd(a)
print s
A = numpy.dot(U[:,0:2],numpy.dot(numpy.diag(s[0:2]),Vh[0:2,:]))
aa = A.reshape((400,))plt.subplot(221,aspect='equal')
plt.plot(x, np.sin(x))
plt.title("sin")plt.subplot(222,aspect='equal')
plt.plot(x, np.sin(x) + ss)
plt.title("sin with noise")plt.subplot(223,aspect='equal')
plt.title("sin remove noise x = 2")
plt.plot(x, aa)A = numpy.dot(U[:,0:1],numpy.dot(numpy.diag(s[0:1]),Vh[0:1,:]))
aa = A.reshape((400,))
plt.subplot(224,aspect='equal')
plt.title("sin remove noise x = 1")
plt.plot(x, aa)plt.show()

第一副图是纯sin波形，第2副图是加了噪声的波形，第三副选择2个奇异值重构A结果很接近标准sin波形实现了去噪，第四副图是选了1个奇异值重构A的结果。

参考文献

http://liao.cpython.org/scipy06.html

https://www.cnblogs.com/jclian91/p/8024101.html

https://blog.csdn.net/m0_50572604/article/details/121018988

https://www.cnblogs.com/pinard/p/6239403.html

https://www.cnblogs.com/pinard/p/6251584.html

https://github.com/Gaoshiguo/PCA-Principal-Components-Analysis