题目描述

原题链接：291. 蒙德里安的梦想

解题思路

（1）状态压缩dp先导知识

状态压缩会用二进制位来存储状态信息，在状态计算时，将整数转化为二进制爹形式进行计算。


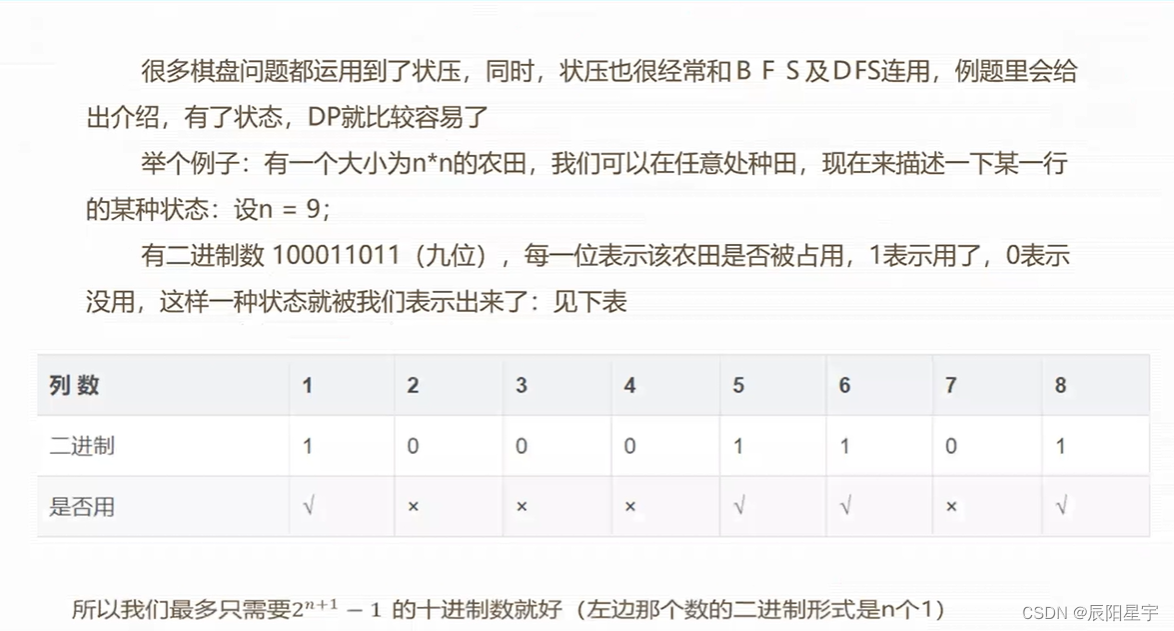
可表示的状态就是 2n2^n2n 个。

（2）题目分析

因为已经规定长方体的规格为1×2，摆放方式只有横着摆放和竖着摆放两种。我们可以先让长方体横着摆放，剩余空余位置竖着摆放，然后看哪些位置摆放情况可以让竖着摆放的长方体填满整个方框即可。

因此，本问题就转化为了，找到合法的横着摆放长方体的情况总数。

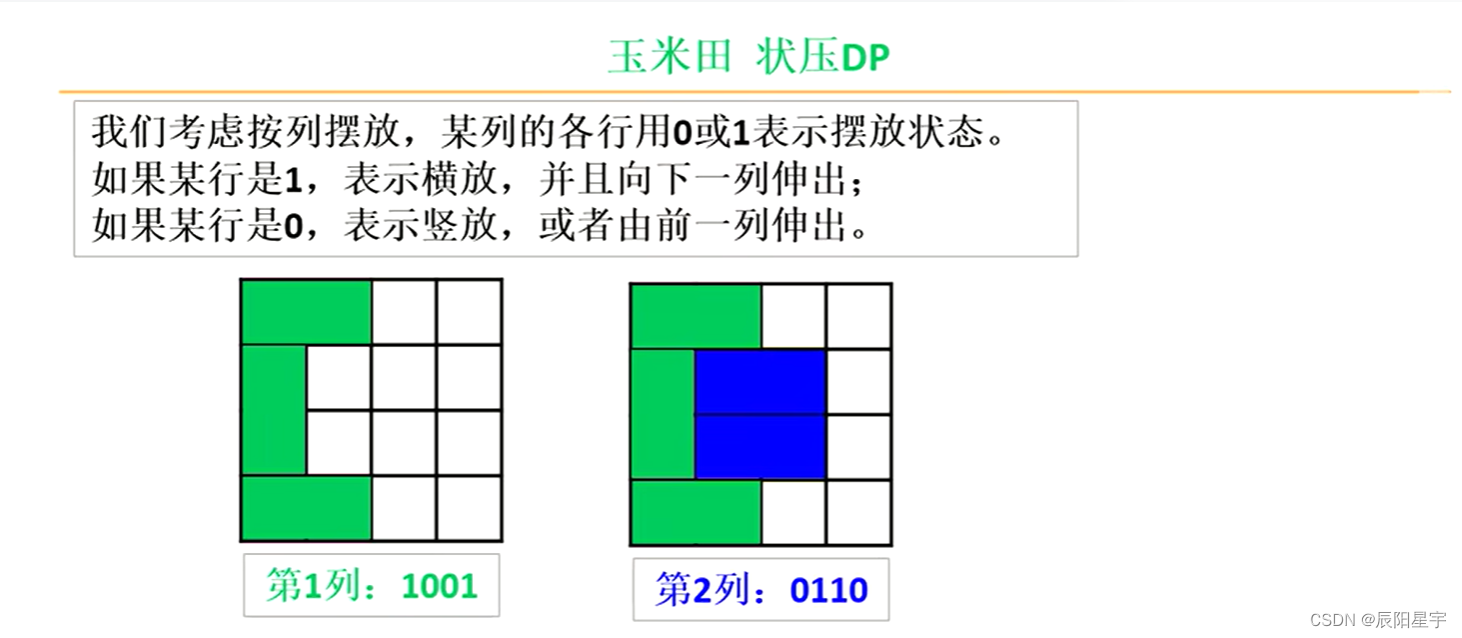
此时规定，当第j列、第i行为1时，代表从当前位置横着新摆放一个长方体（此时第j+1列、第i行，会由第i列伸出一个长方体）。而当第i列、第j行为0时，代表当前位置没有横着新摆放一个长方体。

因此，对于合法摆放位置的规定：
（1）第j -1列和第j列没有的长方体没有出现重叠

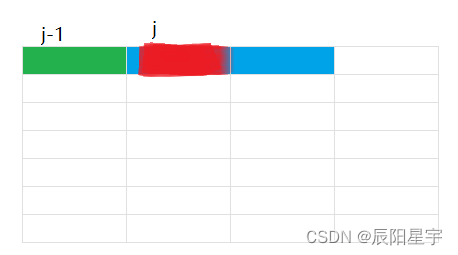
此时由于第j-1列新横放的方块和第j列新横放的方块出现重叠，因此此状态不合法。

（2）第j列的空格数为偶数个

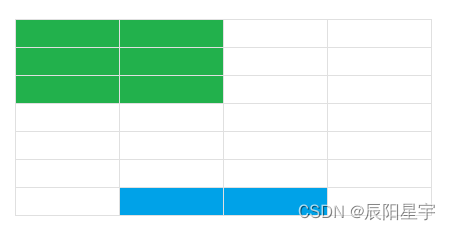
此时第j列的空格数不为偶数个，而是奇数个，就会导致1×2的长方体一定不能填充满这一列，因此此状体不合法。

根据上述的讨论情况，就确定了这样子的dp解法。

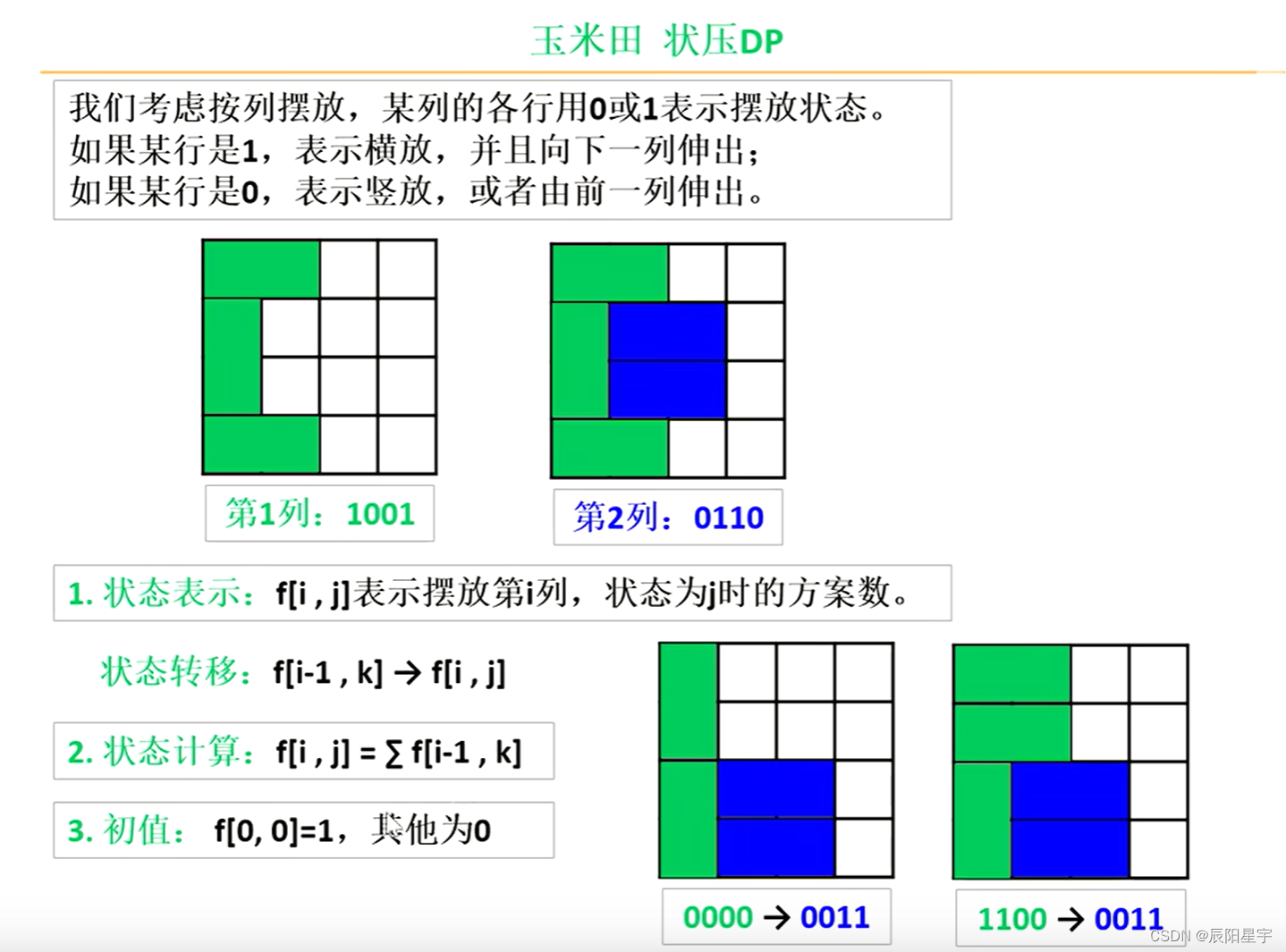
• 动态规划五步曲：

（1）dp[i][j]含义： 第i列处，状态为j时，合法的方案数。

（2）递推公式： f[i,j]=∑02n−1f[i−1,k]f[i, j] = \sum_0^{2^n-1} f[i - 1, k]f[i,j]=∑02n−1​f[i−1,k]，表示从第i-1列到达第i列，可转化为状态j的所有合法状态求和。

（3）dp数组初始化： dp[0][0] = 1，代表第0列不横着放，此时有且仅有一种方案。

（4）遍历顺序： 从左到右，从上到下。

（5）举例：

（3）详细代码

#include 
#include using namespace std;const int N = 12, M = 1 << N;
long long  dp[N][M];		// 数据量大，采用long long
bool state[M];              // 用于记录该状态是否合法（有偶数个0则合法）
int n, m;int main() {// 输入行列，若有一个为0，则退出while(cin >> n >> m, n || m) {// 1、预处理：根据列值化成二进制值，预先判定合法的横着摆放位置，每次枚举所有行，枚举完所有的合法状态for(int i = 0; i < 1 << n; i++) {       // 1 << n：对n进行二进制化，相当于是化成了2^n，让i从0遍历到2^n-1，查询各个状态state[i] = true;                    // 先假设当前摆放情况合法int cnt = 0;                        // 记录当前状态下有多少个连续的0（若有奇数个0，则这几个空位置无法用竖着的长方体填满，不合法）for(int j = 0; j < n; j++) {        // j从0~n，用于依次对当前的i进行移位，来获取最后一位的信息进行一些判定if(i >> j & 1) {                // i >> j：将i左移位j位，判定左移后最后一位是否为1（若为1说明该处新横放有长方体）if(cnt & 1) {               // 再判定摆放长方体之前的位置是否为奇数个0，若为奇数个0，则不合法，标记状态后跳出state[i] = false;break;}} else {                        // 若左移后最后一位不为1，则说明当前位置没有横着新放长方体cnt++;}}if(cnt & 1)         state[i] = false;   // 判定到达最后一个位置时是否合法，也为偶数个0（因为在做上面最后一次for循环时，可能会cnt++后变为奇数）}// 2、dp数组初始化memset(dp, 0, sizeof dp);                   // 初始化dp为0dp[0][0] = 1;                               // dp[0][0]：第0列，状态为0时，表明没有一个横着放长方体，此时有且仅有一种情况。// 3、进行状态计算for(int i = 1; i <= m; i++) {                       // 按列进行遍历，枚举完所有列for(int j = 0; j < 1 << n; j++) {               // 枚举第i列的状态jfor(int k = 0; k < 1 << n; k++) {           // 枚举第i-1列的状态k// 判定第i-1列的状态k能否转移到第i列的状态j：// (j & k) == 0：判定第i列和i-1列是否无重叠，无重叠则合法返回true，有重叠则不合法返回false// state[j | k] : 其中 j | k 相当于是进行异或后让第i-1列新摆放的长方体和第i列新摆放的长方体都出现，看剩余位置能否由竖着摆放的长方体填满if((j & k) == 0 && state[j | k]) {      dp[i][j] += dp[i - 1][k];           // 满足转移条件，则当前的状态情况加上由dp[i-1][k]转化来的情况}}}}cout << dp[m][0] << endl;               // 在摆放位置为0~m-1，合法的第m列应该是从m-1列没有方块伸出到第m列}return 0;
}

问题一：为什么dp遍历时，先遍历j后遍历k可表示先遍历第i列，再遍历第i-1列的状态？

答：因为我们要求的是从第i-1列转化到第i列是的所有合法状态，因此先for循环j时，代表我们的目标列i此时的状态为j，再for循环k里表示从0-2^n-1的各个合法状态，此时从逻辑上 就相当于从第i-1列到第i列的所有的状态匹配情况，当匹配到合法状态时，就进行状态计算。

问题二：为什么遍历pd时，i从1开始？
因为在里面计算状态计算时，默认会是i-1和i进行比较，因此最外for从i开始。

参考视频：9.93 蒙德里安的梦想 状态压缩DP——信息学竞赛培训课程