L1正则化与L2正则化

创始人

2024-06-01 03:09:44

0次

1.1-范数，2-范数

1-范数: $||X||_1=|x|_1+|x|_2+...+|x|_n$
2-范数: $||X||_2 = (|x|_1^2+|x|_2^2+...+|x|_n^2)^{1/2}$ 2-范数就是通常意义下的距离

2.L1和L2正则化

我们所说的正则化，就是在原来的loss function的基础上，加上了一些正则化项或者称为模型复杂度惩罚项。现在我们还是以最熟悉的线性回顾为例子。

优化目标:

$min\frac{1}{N}\sum_{i=1}^{N}{(y_i-w^Tx_i)}^2$

加上L1正则项

$min\frac{1}{N}\sum_{i=1}^{N}{(y_i-w^Tx_i)}^2+C||w||_1$

加上L2正则项

$min\frac{1}{N}\sum_{i=1}^{N}{(y_i-w^Tx_i)}^2+C||w||_2^2$

我们的目标时使损失越小越好。

那加了L1正则化和L2正则化之后，对目标函数的求解有什么作用呢？

3.L1和L2正则化作用

假设X为一个二维样本，那么要求解的参数w也是二维:

原函数曲线等高线(同颜色曲线上，每一组w1,w2带入值都相同)

加入L1和L2正则化的函数图像

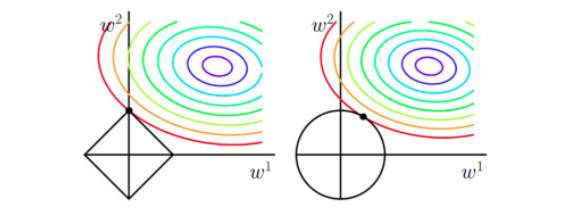
从上面两幅图中我们可以看出:

如果不加L1和L2正则化的时候，对于线性回归这种目标函数凸函数的话，我们最终的结果就是最里面的紫色的小圈圈等高线上的点。
当加入L1正则化的时候，我们先画出|w1|+|w2|=F的图像，也就是一个菱形，这些曲线上的点算出来的1范数|w1|+|w2|都为F。那现在的目标不仅是原曲线算的值要小，即越来越接近中心的紫色圆圈，还要使得这个菱形越来越小(F越来越小)。那么还和原来一样的化，过中心紫色圆圈的那个菱形明显很大，因此我们要取到一个恰好的值。那么如何求值呢？

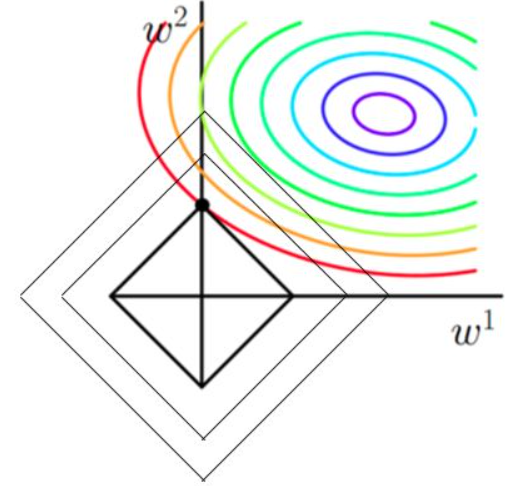
3.1 为什么说菱形和等高线相切的时候损失最小？

以原目标函数的曲线来说，在同一条等高线上，以最外圈的红色等高线为例。我们可以看到，对于红色曲线上的每个点都可以做一个菱形，根据上图3可知，当这个菱形和某条等高线相切的时候，这个菱形最小。

证明:同一等高线上的点能够使得 $\frac{1}{N}\sum_{i=1}^{N}(y_i-w^Tx_i)^2$ 值相同，但是在相切的时候C||w||小，即|w1|+|w2|小，所以能够使得 $\frac{1}{N}\sum_{i=1}^{N}(y_i-w^Tx_i)^2+C||w||_1$ 更小。

那么加入L1范数得到的解，一定是某个菱形和某条原函数等高线的切点。

3.2为什么加入L1正则化的解更容易稀疏?

我们可以观察到，几乎对于很多原函数等高线，和某个菱形相交的时候容易相交在坐标轴上，即最终结果解的某个维度极其容易为0，比如上图最终解释w=(0,x)，这也就是我们所说的L1更容易得到稀疏解(解向量中0比较多)的原因。

证明:假设只有一个参数为w，损失函数为L(w),分别加上L1正则项和L2正则项后有:

$J_{L1}(w)=L(w)+\lambda|w|$

$J_{L2}(w)=L(w)+\lambda|w|^2$

假设L(w)在0处的导数为 $d_0$ ,即

$\frac{\partial L(w)}{\partial w}| _{w=0}=d_0$

则可以推导使用L1正则和L2正则时的导数。

引入L2正则项，在0处的导数

$\frac{\partial J_{L2}(w)}{\partial w}| _{w=0}=d_0+2*\lambda*w=d_0$

引入L1正则项，在0处的导数

$\frac{\partial J_{L1}(w)}{\partial w}| _{w=0^-}=d_0-\lambda$

$\frac{\partial J_{L1}(w)}{\partial w}| _{w=0^+}=d_0+\lambda$

可见，引入L2正则时，代价函数在0处的导数仍然时d0，无变化。

而引入L1正则后，代价函数在0处的导数有一个突变。从d0+λ到d0-λ，如果d0+λ和d0-λ异号，则会在0处会是一个极小值。因此，优化时，很可能优化到该极小值点上，即w=0处。

这里只解释了有一个参数的情况，如果有更多的参数，也是类似的。因此，用L1正则更容易产生稀疏解。

3.3 加入L2正则化的结果

当加入L2正则化的时候，分析和L1正则化是类似的，也就是说我们仅仅是从菱形变成了圆形而已，同样还是求原曲线和圆形的切点作为最终解。当然与L1范数比，我们这样求得L2范数得从图上来看，不容易交在坐标轴上，但是仍然比较靠近坐标轴。因为这也就是我们经常说得，L2范数能让解比较小(靠近0)，但是比较平滑(不等于0)。

综上所述，我们可以看见，加入正则化项，在最小化经验误差得情况下，可以让我们选择解更简单(趋向于0)的解。

从Bayes角度来看，L1,L2正则相当于对模型参数引入先验分布：

L1正则:模型参数服从拉普拉斯分布，对参数加入分布约束，大部分取值为0.

特征选择：稀疏性(权值稀疏)

鲁棒性：忽略异常点

L2正则：模型参数服从高斯分布，对参数加了分布约束，大部分取值很小。

解决过拟合

易优化和计算(权值平滑)

稳定性好

对异常点敏感:误差取平方后放大。

稳定性比较解释

L1存在ill condition(病态)问题：输入发生微小变化导致输出发生很大改变。

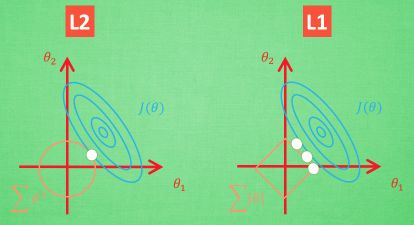
对L1的病态问题大概理解一下，如上图所示，用批数据训练，每次批数据都会有稍稍不同的误差曲线。L2针对这种变动，白点的移动不会太大，而L1的白点则可能跳到许多不同的地方没因为这些地方的总误差都是差不多的。侧面说明了L1解的不稳定性。

https://www.cnblogs.com/lyxLearningNotes/p/16143387.html

L1 与 L2 正则化 - 简书

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：Python3-面向对象

下一篇：运营新人必看 eBay申诉的最全资料