数论----质数的求解(C/C++)
CSDN的uu,你们好呀,今天我们要学习的内容是数论哦!这也是算法题中的一类题目吧。记好安全带,准备发车咯!🚀
学习数论的意义📢
算法导论说:“数论曾经被视为一种虽然优美但却没什么用处的纯数学学科。如今,数论算法已经得到了广泛的使用。这很大程度上要归功于人们发明了基于大素数的加密方法。快速计算大素数的算法使得高效加密成为可能,而目前其安全性的保证则依赖于缺少高效将合数分解为大素数之积(或求解相关问题,如计算离散对数)方法的现状。” 数论可以分为:初等数论,解析数论,代数数论,几何数论等。我们从基础开始学起哦!
求解区间内的质数📗
我们先来看看质数的定义:在大于1的整数中,如果一个整数只包含1和本身两个约数,那么这个数就被称为质数或者素数。
顺便来看看约数的定义:约数(又称因数)是指若整数a除以整数b(b≠0)除得的商正好是整数而没有余数,就说a能被b整除,或b能整除a,其中a称为b的倍数,b称为a的约数。 下面我们就讲讲如何求解一个区间内的所有质数。
2.1 质数的定义求解1-N之间的质数1️⃣
在讲解这种方法之前我们需要直到如何判断一个数是否是质数。根据质数的定义,显然我们可以枚举
2-(N-1)之间数,如果某个数能被N整除,说明N不是质数。反之如果2-(N-1) 之间的数均不能被N整除那么说明N就是质数啦!

在知到了如何判断一个数是否为质数之后,想要求解1-N之间的所有质数只需要遍历 1- N 之间的所有数,用质数的判断函数对这些数进行检验输出即可!
bool isPrime(int x)
{//如果小于2非质数if (x < 2)return false;//遍历 2 - (x - 1)的所有数for (int i = 2; i < x; i++){//如果有约数,非质数if (x % i == 0)return false;}//没有约数返回falsereturn true;
}int main()
{for (int i = 1; i <= 100; i++){//是质数输出结果if (isPrime(i))printf("%d ", i);}return 0;
}
显然在 isPrime 这个函数的枚举中是可以优化的。因为一个数 i 如果能被 n整除,那么 n / i 也能够被n整除,所以我们只需要枚举较小的那个数i即可,也就是for循环结条件可以写成:
for(int i = 2; i <= x / i; i++)
这便是i<=sqrt(x) 的由来!但是这里不建议将循环的结束条件写成:i<=sqrt(x),这样写每一次循环都要进行计算,时间复杂度会提高!也不建议写成:i * i <= x,这样写可能会溢出!发生意想不到的结果。
bool isPrime(int x)
{//如果小于2非质数if (x < 2)return false;//遍历 2 - (x - 1)的所有数for (int i = 2; i <= x / i; i++){//如果有约数,非质数if (x % i == 0)return false;}//没有约数返回falsereturn true;
}int main()
{for (int i = 1; i <= 100; i++){//是质数输出结果if (isPrime(i))printf("%d ", i);}return 0;
}时间复杂度分析:在判断一个数是否为质数时,时间复杂度一定是根号x,求解的数的范围是 1-N
所以总的时间复杂度为:O(N*sqrt(N))。
2.2 筛质数----埃氏筛法2️⃣
什么是筛质数呢?就是将质数从一个区间内筛选出来!你可以将指数理解为较大的石头,合数理解为较小的石头,我们利用筛子就可以将小石头筛掉留下大石头!
第一种方法:
遍历2-N之间的所有数,将遍历到的该数的倍数(不包括自身)筛去,遍历完毕后剩下的数就是质数啦!

如何对应到代码上呢?我们用一个数组primes来存储质数,用一个数组st来判断一个数是否被筛去,然后我们遍历1-N之间的所有数,如果这个数没有被筛去,即st[i] == false,就把他添加到primes数组中!然后利用这个数将他的倍数筛去!
时间复杂度分析:

所以我们可以取时间复杂度为N*logN。
const int N = 100;
bool st[N];
int primes[N];void getPrimes(int n)
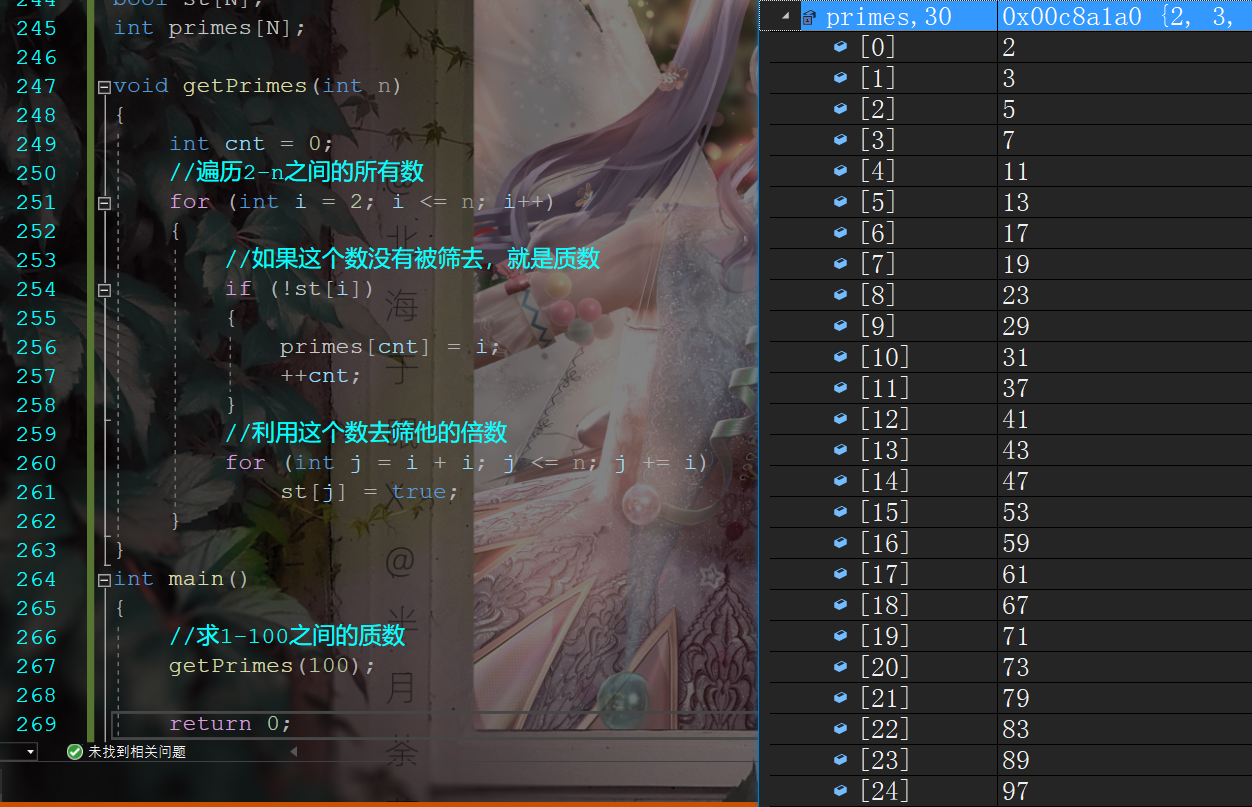
{int cnt = 0;//遍历2-n之间的所有数for (int i = 2; i <= n; i++){//如果这个数没有被筛去,就是质数if (!st[i]){primes[cnt] = i;++cnt;}//利用这个数去筛他的倍数for (int j = i + i; j <= n; j += i)st[j] = true;}
}
int main()
{//求1-100之间的质数getPrimes(100);return 0;
}
方法一的优化:
筛选的过程中我们只需要筛掉质数的倍数即可!因为合数是可以进行质因子分解的!所以所有的合数一定会被他的质因子给筛掉!因此我们可以把筛掉倍数的循环放在里面!
const int N = 100;
bool st[N];
int primes[N];void getPrimes(int n)
{int cnt = 0;//遍历2-n之间的所有数for (int i = 2; i <= n; i++){//如果这个数没有被筛去,就是质数if (!st[i]){primes[cnt] = i;++cnt;//利用这个数去筛他的倍数for (int j = i + i; j <= n; j += i)st[j] = true;}}
}
int main()
{//求1-100之间的质数getPrimes(100);return 0;
}时间复杂度分析:
这里有一个质数定理:1-N中的质数个数有 N / lnN 个。

2.3 筛质数----线性筛法3️⃣
线性筛法是对埃氏筛法的优化哈!我们来看埃氏筛法:对于6和12这两个数,在遍历到质数2时这两个数会被筛一次,在遍历到质数3时这两个数还会再被筛一次!显然会有重复的工作!而线性筛法能够保证每一个合数只会被筛一次,这是怎么做到的呢?
我们来看这样一句话:对于一个合数X,假设primes[j] 是X的最小质因子,那么在遍历到质数primes[j] 时,这个合数X就一定会被筛去,又因为每一个合数都有且仅有一个最小质因子,所以对于每一个合数我们都用它的最小质因子来筛掉!
具体应该怎么做呢?同样我们用i遍历1-N之间的所有数,如果这个数没有被筛去,那么他就一定是质数,然后我们用j从小到大遍历存储质数的primes数组,然后筛掉primes[j] * i这个合数!为什么是primes[j] * i 呢?

那么用j遍历primes数组中的质数时循环的结束条件是什么呢?通过上面的分析,我们能够知道退出遍历primes数组的条件就是用最小质因子筛去所有可能筛掉的数!当遍历得到的质数如果比i大的话,显然就不满足用最小质因数筛合数的条件了!因此循环的结束条件可以这么写:
for(int j = 0; primes[j] <= n / i; j++)这里大家可能会有一个疑问?primes数组的访问会不会越界呢?也就是说要不要加上小于primes数组大小的限制条件呢?
emm,是没有这个必要的哈!当i为合数时,枚举到他的最小质因子后就会结束循环!当i为质数的时候,枚举到自身时也会退出循环,所以是没有必要加上这个条件的哈!
const int N = 100;
bool st[N];
int primes[N];void getPrimes(int n)
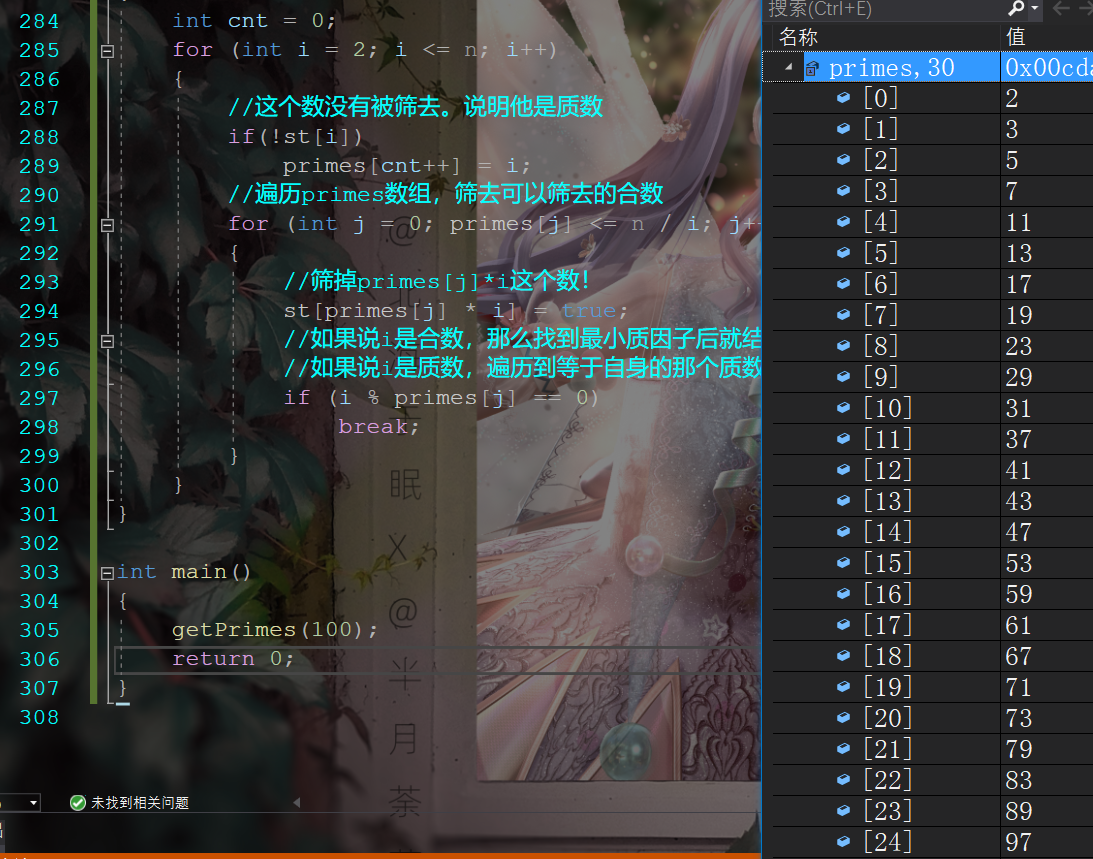
{ int cnt = 0;for (int i = 2; i <= n; i++){//这个数没有被筛去。说明他是质数if(!st[i])primes[cnt++] = i;//遍历primes数组,筛去可以筛去的合数for (int j = 0; primes[j] <= n / i; j++){//筛掉primes[j]*i这个数!st[primes[j] * i] = true;//如果说i是合数,那么找到最小质因子后就结束循环//如果说i是质数,遍历到等于自身的那个质数时也会结束循环if (i % primes[j] == 0)break;}}
}int main()
{getPrimes(100);return 0;
}
3. 埃氏筛法和线性筛法粗略的时间比较⌛
当数据量在10的6次方时两者时间相差不大,数据量在10的7次方时,埃氏筛法会比线性筛法慢一倍左右。
数据量为10^6时:
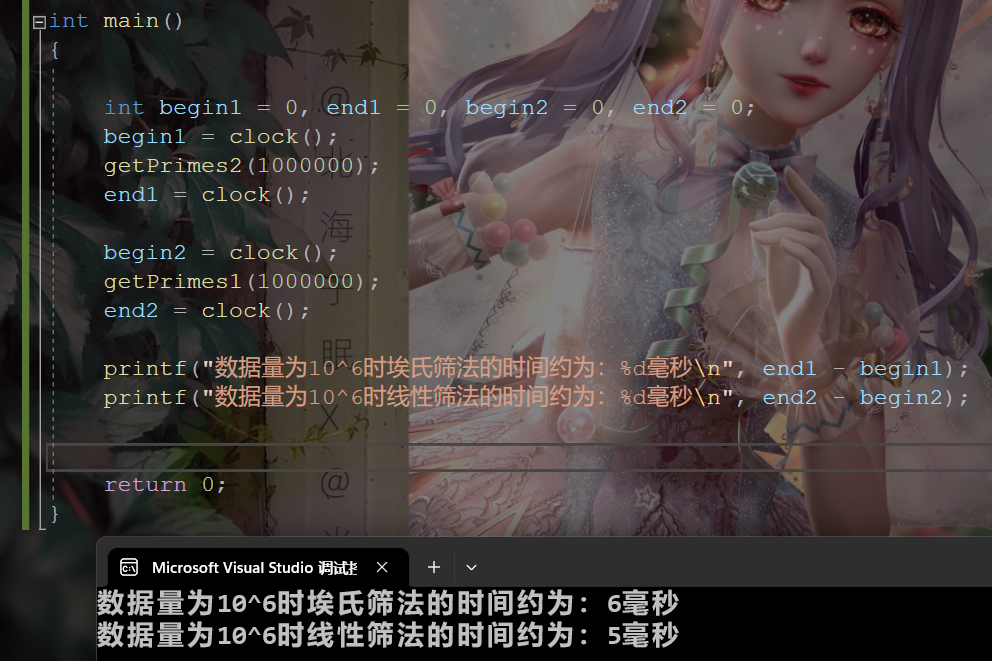
数据量为10^8时:
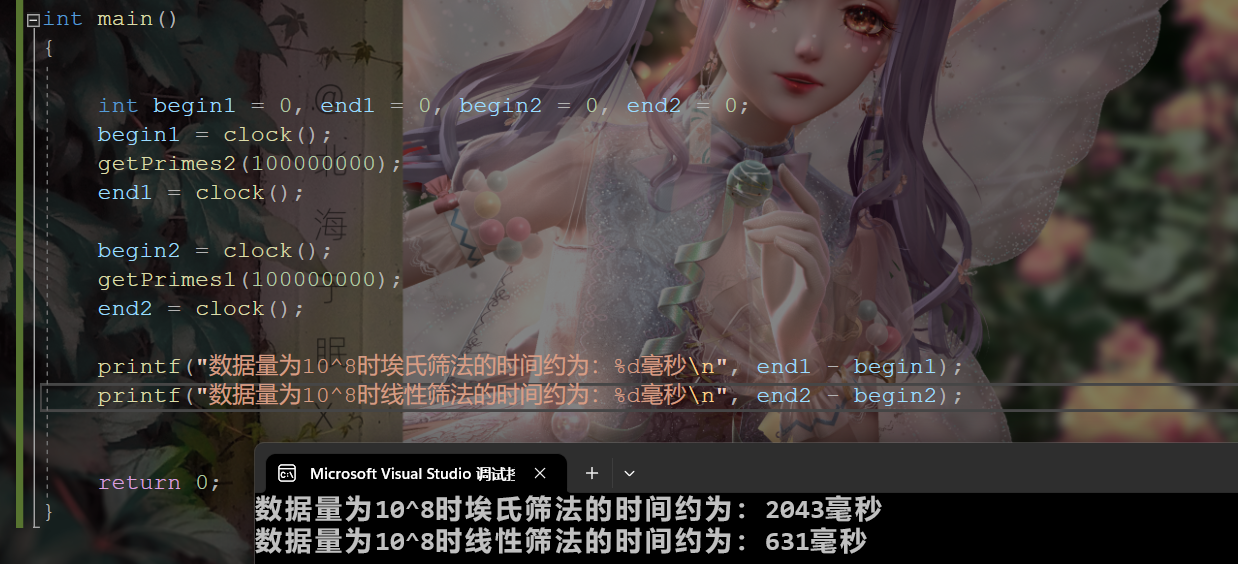
3. 小试牛刀🚩
204. 计数质数 - 力扣(Leetcode)
谢谢大家的阅读!如果有什么讲的不对的地方欢迎大家指正!💐
